做好闭环(四):二分答案算法的代码统一结构
文章目录
你好,我是胡光。
不知不觉,我们已经讲完了“算法数据结构篇”的全部内容。说是“讲完”,其实更意味着你的算法数据结构的学习之路才刚刚开始,因为编程的核心与灵魂就是算法和数据结构。但这毕竟是一个入门课,所以,整个这部分的内容,我更多是侧重说说那些你可能比较陌生的,且有趣的思维与结构。
我希望通过这个过程,能够激起你对于算法数据结构的学习热情。时至今日,我相信你应该更能深刻地理解我在开篇词里说到的,“学编程,不等于学语言“这句话的含义。
我也非常高兴,看到很多同学都在紧跟着专栏更新节奏,坚持学习。经常在专栏上线的第一时间,这些同学就给我留言,提出自己的疑惑。大部分留言,我都在相对应的课程中回复过了,而对于每节课中的思考题呢,由于要给你充足的思考时间,所以我选择在今天这样一节课中,给你进行一一的解答。
看一看我的参考答案,和你的思考结果之间,有什么不同吧。也欢迎你在留言区中,给出一些你感兴趣的题目的思考结果,我希望我们能在这个过程中,碰撞出更多智慧的火花。
重新认识数据结构(上):初识链表结构
在这一节里,我们学习了基本的链表结构,并且演示了链表结构的插入操作。最后呢,给你留了一个题目,就是实现链表的删除操作。留言区中很多人实现的代码,我也都看过了,总的来说,很多用户对“虚拟头结点”的掌握还是很不错的,下面是我给出的参考代码:
struct Node *erase(strcut Node *head, int ind) {
struct Node ret, *p = &ret, *q;
ret.next = head;
while (ind–) p = p->next;
q = p->next;
p->next = p->next->next;
return ret.next;
}
由于删除操作,有可能删除的是 head 所指向链表的头结点,所以代码中使用了虚拟头结点的技巧来实现。其中,细心的你可能会发现一个致命的问题:删除节点的操作中,我们只是改变了链表节点的指向关系,跳过了那个待删除节点的位置,那原先那个待删除节点呢?这个节点的空间呢?
这就涉及到操作系统中的内存管理相关的知识了,由于这里不影响编程逻辑的理解,所以,我们就不展开说了。如果你感兴趣,可以自行搜索:内存泄漏、malloc、free 等关键字进行学习。
重新认识数据结构(下):有趣的“链表”思维
这一节是上一节链表知识的升华,我们将一个快乐数序列,在思维层面映射成了链表结构,之后就将快乐数的判定问题,很自然的转换成了链表判环问题,算是彻彻底底的体验了一把链表思维。最后呢,我留了两个思考题,下面我给你一一解答。
1. 计算环的长度
第一个问题,如果链表中有环的话,那么这个环的长度是多少?这个问题比较简单,我看到留言区中很多用户都能自行想出来,在这里我就简单说一说。
我们可以肯定,如果链表中有环,那么采用快慢指针的方法,两个指针一定会在环中相遇。此时,可以让其中一个指针不动,另外一个指针再沿着环走一圈,直到两个指针再次相遇,这样,就能得到环的长度了。
2. 找到环的起始位置
第二个问题,如果链表中有环,请求出环的起始点。如下图所示,环的起始点为 3 号点。

图 1:链表成环示意图
这里呢,我将用图跟你感性地解答这个问题,请你注意,以下我所要讲的不是一个严格的证明过程,如果想要更准确地理解这个问题,你可以试着借助“同余式”来理解。下面,就开始我们的非严谨图例演示。
首先,假设从链表起始点到环的起点距离为 x,那么当快慢指针中的慢指针 p 刚刚走到环的起始点位置的时候,q 指针应该在环内部距离环起始点 x 的位置上,如图所示:
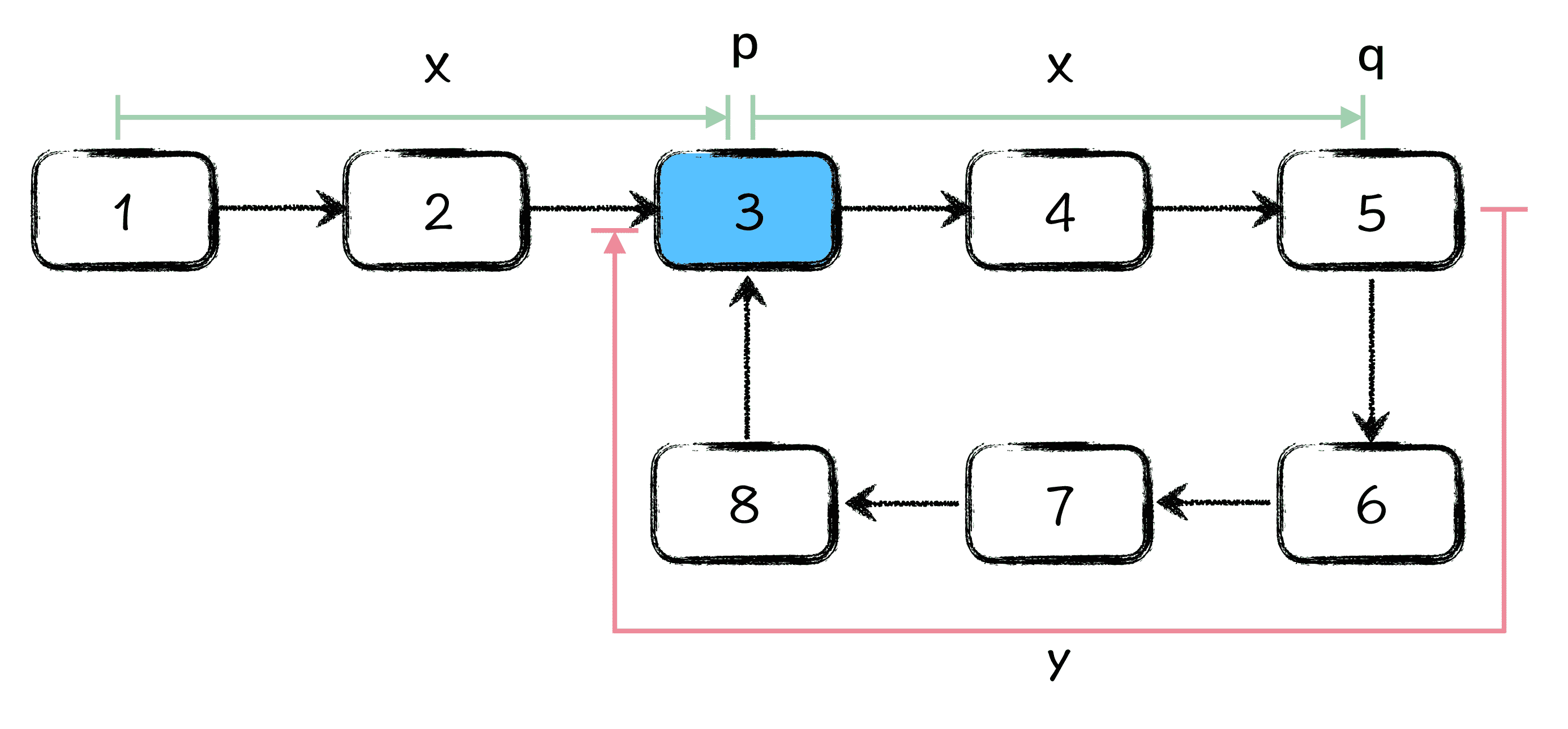
图 2:p 节点刚刚进入环时刻
图中,q 指针距离环起始点 x 步,q 指针沿着链表向前走 y 步,就又可以到达环的起始点位置,如图所示 x + y 等于环长。也就是说,q 指针想要遇到 p 指针,就必须要追上 y 步的距离,又因为 p 指针每次走 1 步,q 指针每轮走 2 步,所以 q 指针每轮追上 1 步,也就是说,从此刻开始,当 q 指针追上 p 指针的时候,p 指针正好向前走了 y 步,如图所示:

图 3:p、q 环中相遇时刻
此时,你会发现 p 点在环中走了 y 步以后,p 和 q 相遇了,也就意味着 p 点再走 x 步就到环的起始点了。而恰巧,从链表头结点开始到环的起始点也是 x 步,所以此时只需要让 p 站在相遇点,q 指针回到链表的起始点,然后两个指针以相同的速度,一起往后走,直到二者再次相遇的时候,相遇点就是环的起始点了。
至此,我们就看完了求解环起始点位置的方法,至于代码么,就不是难题了,你可以自行发挥了。
二分查找:提升程序的查找效率
这一节中呢,我们学习了简单的二分查找算法,由此我们引申出了二分答案的相关算法。二分答案算法的应用场景呢,就是有一个函数 f(x) = y,如果它具有单调性,并且通过 x 求 y 很好求,而通过 y 确定 x 就很麻烦,这时,二分答案算法就该登场了。
最后的思考题中呢,是一道通过税后工资,计算税前工资的题目。我们可以发现,根据个人所得税缴纳的规则,肯定是税前工资越高,税后工资就越高,所以我们把税前工资 x 和税后工资 y 之间,看成是一个映射关系 f 的话,那么 f(x) = y 的函数,就是单调函数。
而这个 f 函数呢,我们也可以看到,通过税前工资 x 确定税后工资 y 的过程很简单,而通过税后工资 y 计算税前工资 x 的过程就不那么容易了。因此,我们当然要搬出二分答案算法,来解决这个问题了。下面是我给出的示例代码:
#define EPS 1e-7
#define min(a, b) ((a) < (b) ? (a) : (b))
double f(double x) {
double xx = min(3000, x) * 0.03;
if (x > 3000) {
xx += (min(12000, x) - 3000) * 0.1;
}
if (x > 12000) {
xx += (min(25000, x) - 12000) * 0.2;
}
if (xx > 25000) {
xx += (min(35000, x) - 25000) * 0.25;
}
return x - xx;
}
double binary_search(double l, double r, double y) {
if (r - l <= EPS) return l;
double mid = (l + r) / 2.0;
if (f(mid) < y) return binary_search(mid, r, y);
return binary_search(l, mid, y);
}
你会发现,代码中的 binary_search 函数,和我们那一讲中所给的切绳子问题的代码几乎一模一样,唯一不同的就是 f 函数换了样子。
其实对于二分答案的算法实现,代码真的不是什么难点,难点在于发现问题可以采用二分算法的过程。也就是看到那两条性质判断:f(x)=y 是不是具有单调性;是不是通过 x 求 y 比较容易,通过 y 求 x 比较困难。
栈与单调栈:最大矩形面积
本节呢,我们学习了栈和单调栈的基本知识,并且知道了单调栈是用来维护最近大于或小于关系的数据结构。最后的思考题呢,是判断一个括号序列是否是合法的,所谓合法的括号序列,也就是括号之间要么是完全包含,要么是并列无关。
根据栈的基础知识,如果我们把一个元素入栈动作看成是左括号,出栈看成是对应的右括号,那么一组元素的入栈及出栈操作,就可以唯一对应到一个合法的括号序列。例如,如下操作序列:
1 2 3 4 5 6 7 8 9 10
push push pop pop push push pop push pop pop
其中 push 是入栈操作,pop 是出栈操作。显然,3 号的 pop 操作,弹出的应该是 2 号 push 进去的元素,也就是 2 号和 3 号操作是一对操作。那么把 push 写成左括号,pop 写成右括号,如上操作序列,就可以对应如下的括号序列:
【()】{【】【】}
你会发现,相对应的左右括号,就对应了相匹配的 push 和 pop 操作。那么判断一个括号序列是否合法,就可以把这个括号序列看成是一组入栈和出栈操作。
我们依次处理括号序列中的每一位,碰到左括号就入栈;碰到右括号,我们就弹出栈顶的一个左括号,看看是否和当前右括号是匹配的,如果不匹配就说明括号序列非法,如果匹配,就继续处理下一个括号序列中的字符。直到最后,如果栈中为空,就说明原括号序列合法。
好了,至此我们就讲完了这道题目的解题思路,接下来就是请你把我说的解题思路,转换成代码了,加油!如果实在想不出来,也可以参考用户 @胖胖胖、@Hunter Liu 在留言区中的代码和解题思路。
动态规划(下):动态规划之背包问题与优化
在这一节课,我们认识了背包类动态规划算法,讲了 0/1 背包问题,以及多重背包问题转 0/1 背包问题的转换技巧。其中我们提到了用二进制拆分法对多重背包拆分过程进行优化,这样不但可以大大减少拆分出来的物品数量,并且还不影响转换成等价的 0/1 背包问题。
关于动态规划状态定义的相关理解,这里给用户 @徐洲更 点赞,大家可以在《动态规划(上):只需四步,搞定动态规划算法设计》当中看到他的留言。
下面呢,我就给出多重背包转 0/1 背包的示例代码:
#define MAX_N 100
#define MAX_W 10000
int v[MAX_N + 5], w[MAX_N + 5], c[MAX_N + 5];
int v1[MAX_N + 5], w1[MAX_N + 5], n2 = 0;
int dp[MAX_N + 5][MAX_W + 5];
// 添加一个 0/1 背包中的物品
void add_item(int v_value, int w_value) {
n2++;
v1[n2] = v_value;
w1[n2] = w_value;
return ;
}
int get_dp(int n, int W) {
// 对多重背包中的每一种物品进行拆分
for (int i = 1; i <= n; i++) {
// 采用二进制拆分法
for (int k = 1; k <= c[i]; c[i] -= k, k «= 1) {
add_item(k * v[i], k * w[i]);
}
if (c[i]) add_item(c[i] * v[i], c[i] * w[i]);
}
// 按照 0/1 背包的方式进行求解
for (int i = 1; i <= n2; i++) {
for (int j = 1; j <= W; j++) {
dp[i][j] = dp[i - 1][j];
if (j < w1[i]) continue;
if (dp[i - 1][j - w1[i]] + v1[i] < dp[i][j]) continue;
dp[i][j] = dp[i - 1][j - w1[i]] + v1[i];
}
}
return 0;
}
代码中,v、w、c 数组存储的是多重背包中第 i 种物品的价值、重量和数量,v1、w1 数组用来存储拆分出来的 0/1 背包中的物品价值和重量信息,get_dp 函数就是求解多重背包问题的过程。
其中,分成两步进行求解,首先对多重背包中的每种物品,按照二进制拆分法,打包拆分成 0/1 背包中的若干个物品。拆分完成后,再按照 0/1 背包的算法流程进行求解,需要注意的是,代码中的循环变量 k,枚举的就是拆分的每一堆的物品数量,从数量 1 开始,每次扩大一倍。
对于多重背包中的每种物品,经过二进制拆分以后,最后剩下的几个,要单独算作一个物品,这就是代码第 22 行的含义。理解了二进制拆分的过程以后,后面的 0/1 背包的求解过程,就不需要我来解释了,都是老生常谈了。
好了,今天的思考题答疑就结束了,如果你还有什么不清楚,或者有更好的想法,欢迎告诉我,我们留言区见!
文章作者 anonymous
上次更新 2024-05-18