13|程序设计原则:把计算过程交给计算机
文章目录
你好,我是胡光,欢迎回来。
上一节中,咱们说了数学思维对于编程的重要性,并且跟你介绍了一种最重要的程序设计思维:数学归纳法。这个思维,不仅可以帮助我们设计程序,而且还可以帮助我们理解及证明程序的正确性。
不过说了这些数学对编程的重要性,可能你还觉得不过瘾,感觉只是停留在理论层面,还是有一层窗户纸没有捅破。今天呢,我就给你带来一道具体的编程问题,从这个具体的问题中,让你过把瘾。
一道简单的数学题
首先,我们先看一道很简单的数学问题,求出 1000 以内所有 3 或 5 倍数的数字的和。什么意思呢?我们先缩小范围,就是求 10 以内,所有 3 或 5 的倍数。我们很快就能找到,这里有 3、5、6、9,它们相加之和是 23。注意,这里说的是 10 以内,所以不包括 10。
回到 1000 以内这个原问题,这个问题其实很简单,可能你现在就想马上撸起袖子开始写代码了。可别急,听我给你分析分析怎么做,才算是又好又快地用程序,解决这个实际的数学问题。
1. 把计算过程,交给计算机
一个简单的疑问,我们为什么要写程序,让计算机帮我们算这个问题呢?那是因为,计算机的计算速度,比我们人类要快上几百几千倍不止,出错率也比我们要低得多。我们写程序的一个目的,就是减少我们人类在解决问题中的具体计算过程,那什么叫做具体计算过程呢?
例如,当你写一行代码“3 + 5”的时候,这是把计算过程交给了计算机,而如果你直接在程序中写上了 8 这个结果的时候,相当于你自己做了这个计算过程。因此,所谓减少我们的具体计算过程,就是能在程序中写 3 + 5,就写 3 + 5,不要写 8。
这就是我要强调的,要把计算过程交给计算机来做,而不是我们自己来做,毕竟计算机是很擅长做这种事情的,你没必要替它省这个事儿。在这样的指导思想下,我们先来看下面这段程序:
#include <stdio.h>
int main() {
int sum = 0;
for (int i = 1; i < 1000; i++) {
sum += i * (i % 3 == 0 || i % 5 == 0);
}
printf("%d\n", sum);
return 0;
}
这段程序中,循环遍历 1000 以内的所有整数,然后把 3 或 5 的倍数累加到变量 sum 中,最后输出 sum 变量的值,就是 1000 以内,所有 3 或 5 的倍数和。
其中有一个编程技巧,就是利用条件表达式 (i % 3 == 0 || i % 5 == 0) 与数字 i 相乘,条件表达式等于 1 的时候,说明 i 是 3 或 5 的倍数,sum 累加的值就是 i * 1 就是 i 的值;而当条件表达式不成立的时候,sum 累加的值就是 0。掌握这个编程技巧,关键是理解条件表达式的值。
看完了程序的基本逻辑以后,我们来想想,在上述的程序中,有哪个数字,是我们人为计算得到,然后再写到程序中的?你会发现,根本没有。也就是说,我们将所有的计算过程,都交给了计算机,让它来帮我们完成。而我们做的,仅仅是描述这个计算过程,所以这份程序是一份合格的程序。
2. 数学思维:提升计算效率
为什么评价上面的程序,只是一份合格的程序呢?我们想象这么个场景,你是一个老板,手底下有一个工人,你的目的要让工人抬来一桶水。你可能有两种吩咐工人做事的方法:第一种,让工人拿个水瓢,去到 3 里以外,一瓢一瓢的打水,他来来回回跑好几趟,才能打满一桶水。第二种方式,就是你让工人去库房里面拿个水桶,然后再到 3 里以外去打一桶水回来,这样工人只需要跑一趟就能完成任务。
在这两个方法中,第一种工人打满一桶水的效率,明显要差于第二种,而造成这样的结果,是因为你作为老板,教给工人的方法不同,导致效率上的差别。
而在编程中呢,计算机其实就像示例中的工人,你教给它什么方法,它就执行什么方法,任务完成的效率,和计算机没关系,而是和你完成程序,所教给计算机的方法有关系。这个方法呢,就是我们前文中所说的“算法”。
再回到之前那个要求出 1000 以内所有 3 或 5 倍数的数字和的程序,程序虽然完成了任务,可是完成的效率不够高效。
下面我们就把数学类的算法思维,加进程序中,看看效果吧。记住,加入数学思维的同时,也要保证,将计算过程留给计算机。首先来看如下程序:
#include <stdio.h>
int main() {
int sum3 = (3 + 999 / 3 * 3) * (999 / 3) / 2;
int sum5 = (5 + 999 / 5 * 5) * (999 / 5) / 2;
int sum15 = (15 + 999 / 15 * 15) * (999 / 15) / 2;
printf("%d\n", sum3 + sum5 - sum15);
return 0;
}
上面程序中,有三个整型变量分别代表 1000 以内所有 3 的倍数的和 sum3,所有 5 的倍数的和 sum5,和所有 15 倍数的和 sum15。最后呢,用 sum3 + sum5 - sum15 的值,代表了 3 或 5 的倍数的和。你对这个结果可能有点反应不过来,听我继续给你解释。
假设,我们现在手上有两个集合,第一个集合中装的是所有 3 的倍数,第二个集合中装的是所有 5 的倍数,想想两个集合的交集是什么?是不是就是所有 15 的倍数。那么当我们用第一个集合的所有元素和,加上第二个集合中的所有元素和的时候,两个集合交集中的元素,被重复加了一次。所以,最后再减去两个集合交集中的元素和即可。如上所述的程序思路,你可以参考如下示意图。

图 1:问题的集合表示
看完了程序思路以后,我们来具体看一下其中的代码,就拿 sum3 的计算过程来举例,其实使用的就是“等差数列求和公式”,如果你忘了等差数列求和公式,请看下图:
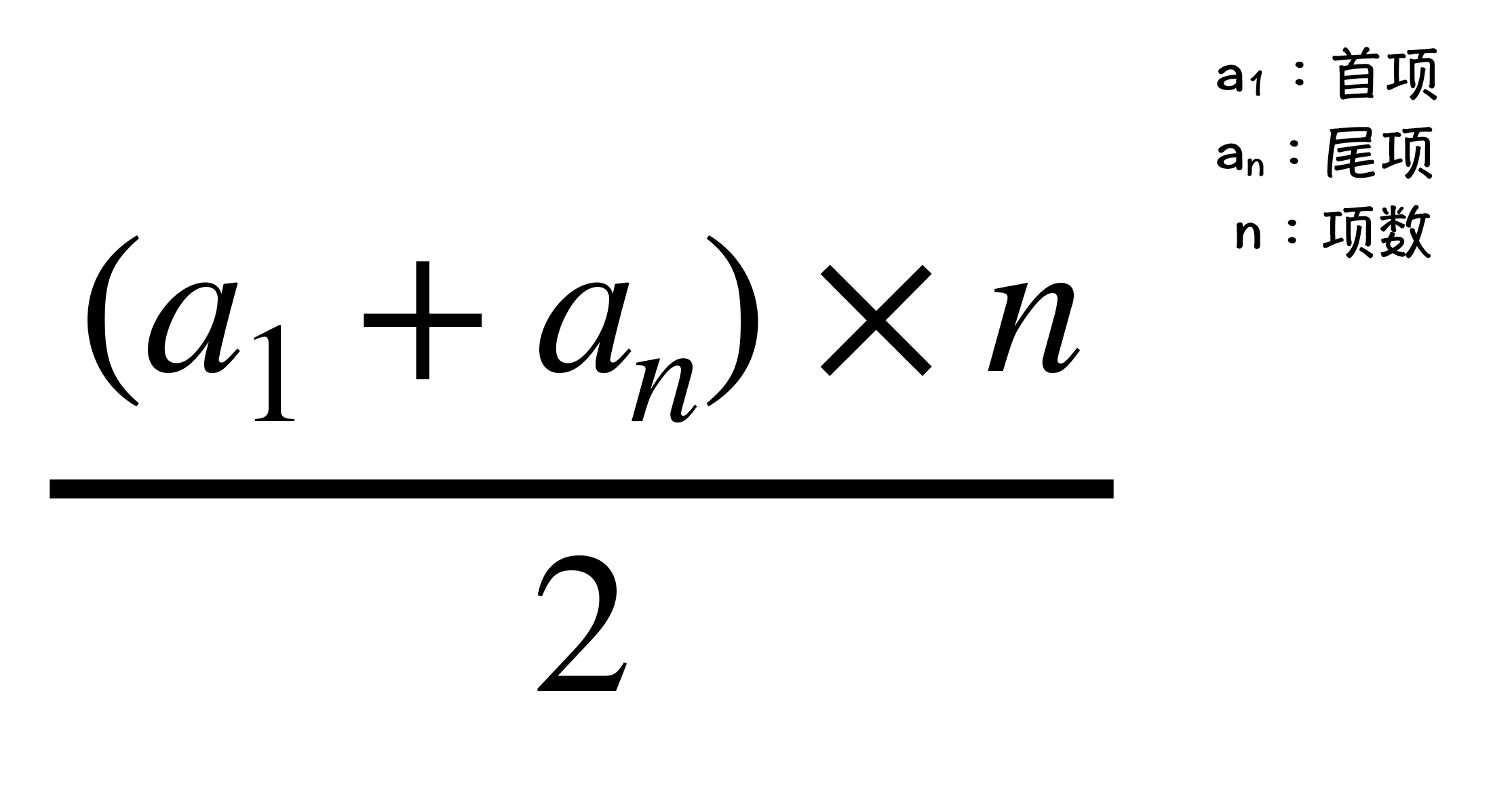
图 2:等差数列求和公式
我们再来回顾一下程序,在编写这个程序的过程中,其中有哪些数字是我们计算得到的么?你会发现没有一个是我们直接计算得到的,哪怕是 5 的倍数 995 这个数字,也是我们通过一段代码算得到的。
而对于这段代码呢,咱们可以详细解释一下,首先用 1000 以内最后一个数字 999 除以 5,会得到在 1000 以内 5 的倍数有多少个。为什么会得到这个结果呢?这个就要说说 C 语言中的整型间的除法问题了。
在 C 语言中,两个整型数字相除,结果会做向零取整,什么是 向零取整呢?解释这个概念之前,先要介绍一下向下取整的概念,所谓向下取整,就是取小于等于当前数字的第一个整数。
例如,4.9 向下取整,就是 4,因为小于等于 4.9 的第一个整数就是 4。那么 -1.5 向下取整等于多少呢?这里需要注意,结果是 -2,不是 -1,因为小于等于 -1.5 的第一个整数是 -2,而 -1 比 -1.5 要大。
当你明白了什么是向下取整以后,就很好理解向零取整了,那就是取当前数字和 0 之间,与前数字距离最近的整数。对于正数来说,向零取整的结果和向下取整的结果相同,而对于负数来说结果恰好相反。
咱们还是拿 -1.5 举例,向下取整是 -2,可是向零取整就不同了,向零取整是在当前数字与 0 之间,取一个距离当前数字最近的整数,取到的就是 -1。
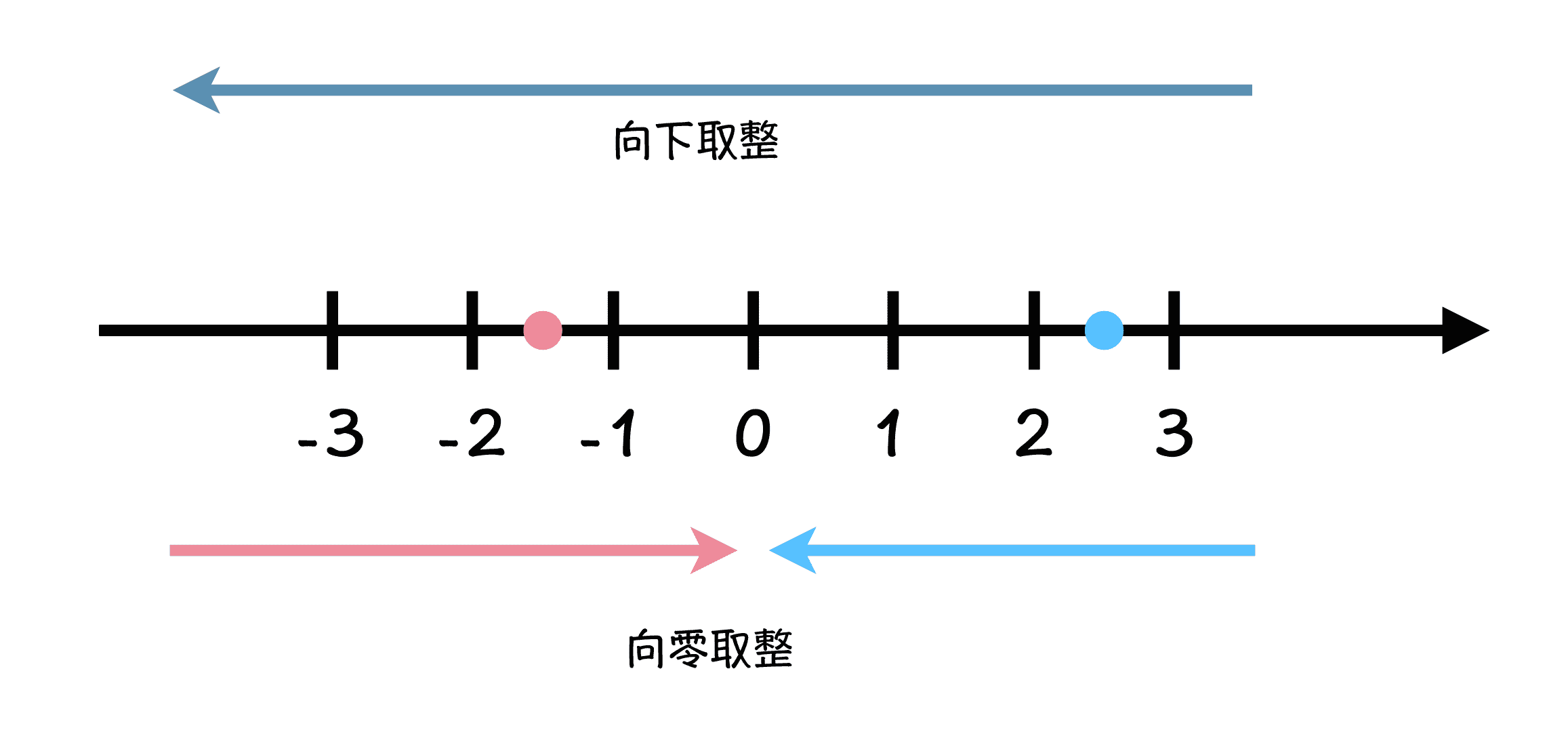
图 3:向下取整与向零取整
理解了 C 语言中的整数除法规则以后,我们再回到题目中看一下,题目中用 999 / 5 得到的就是 1000 以内有多少个 5 的倍数的数字,然后再用这个数字乘以 5 就得到了 1000 以内,最后一个 5 的倍数的数字。
这时候你可能又问了,为什么要这么麻烦呢?何不直接写一个 995 呢?你算得没错,995 确实是 1000 以内最后一个 5 的倍数。可你别忘了,今天我想教给你的是“把计算过程,交给计算机”,也就意味着计算 5 的倍数,可能还轻松一点儿,那要是计算 7 的倍数呢?13 的倍数呢?9973 的倍数呢?你会发现,还是计算机比你更适合做具体的计算。所以记住:将计算过程,留给计算机。
一起动手,搞事情
在做今天的思考题之前,我们先来弄清楚两个说法,“平方和”以及“和的平方”。
例如,10 以内自然数的平方和就是:
1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2 + 7^2 + 8^2 + 9^2 + 10^2 = 385
也就是 1 到 10 每个数字的平方相加之和。
而,10 以内自然数的和的平方就是:
(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10) ^ 2 = 3025
也就是 1 到 10 所有数字相加之和,然后再取平方的值。
思考题:和的平方减平方和
今天我们的思考题呢,分成两个子问题:
1. 请编写一个程序,计算 100 以内自然数“和的平方”与“平方和”的差。
2. 通过今天的学习,我们复习了等差数列求和公式,那你能否通过查阅资料,推导得到等差数列的平方和公式呢?
课程小结
好了,最后我们来做一下今天的课程小结吧。通过今天这个简单的小任务,我希望你记住如下三点:
- 具体的计算过程,计算机比你更擅长,所以请把具体的计算过程,留给计算机。
- 编写程序,其实是在描述和规定计算过程,而描述的方式不同,效率也不同。
- 不同的效率过程,就是我们所谓的不同的算法过程,记住:算法很重要。
关于“算法很重要”这句话,你可能有点儿听腻了,可我还是要强调一遍:所谓算法,叫得上来名字的算法是算法,还有很多叫不上来的名字,其实也是算法。两者放在一起,统一被描述成为“算法思维”。你想掌握一个有名字的算法很容易,可要掌握“算法思维”可就没那么容易了,这是需要很长一段时间的锻炼、总结和积累。
好了,今天就到这里了,不积跬步,无以至千里,希望你在看完本节课后,自己也多加练习体会。我是胡光,我们下期见。
文章作者 anonymous
上次更新 2024-05-18