20|二分查找:提升程序的查找效率
文章目录
你好,我是胡光,欢迎回来。
上节课,我们讲了链表的基础结构,以及体会了一把链表结构在思维逻辑层面的作用,就是面对看似复杂的问题,当我们把它转换成链表结构思维去解决的时候,这些问题和困难都迎刃而解。
今天呢,我将带你学习一种简单、有趣且高效的算法,叫做二分查找。在学习二分查找之前呢,有一个关于二分查找的笑话,你必须知道。
话说,在学校图书馆的计算机科学相关书籍借阅区里面,有一个女生抱着 40 本书往外走,经过图书馆安检机器的时候,安检机器发出了警报声。这时候,女生很无奈,就把书放到了地上,准备一本一本地去试,看看究竟是哪一本书没有消磁。
女生的举动,被旁边图书馆管理员阿姨看到了,阿姨看不下去了,叫住了她,说:这么一本一本的尝试,多慢啊!我教你一种方法。眼看阿姨将书分成两摞,拿起其中一摞的书,过了一下安检,安检机器响了,阿姨就又将这摞书分成了两部分,拿出其中一部分又过了一次安检……就这样,阿姨每次将书的数量减少一半,没几次就找到了那本没有消磁的书。阿姨得意洋洋地说:小姑娘,这就是书中讲的二分查找算法,你这专业知识不过关啊!次日,图书馆发现,丢了 39 本书。
上面这个故事中的阿姨,虽然知道二分查找算法,可明显是对使用算法的前提条件没有搞清楚。今天,我教给你的不仅是二分查找算法本身,还希望你能准确搞清楚二分查找算法的使用场景。
今日任务
在正式开始今天课程之前呢,先来看一下今天这 10 分钟的任务吧。
假设你手上有 n 段长度不等的绳子,你现在想将这些绳子进行裁剪,裁剪出 k 条长度相等的绳子,注意,只能剪断绳子,不能拼接绳子。问题就是,你能得到的这 k 段绳子的最长长度是多长?
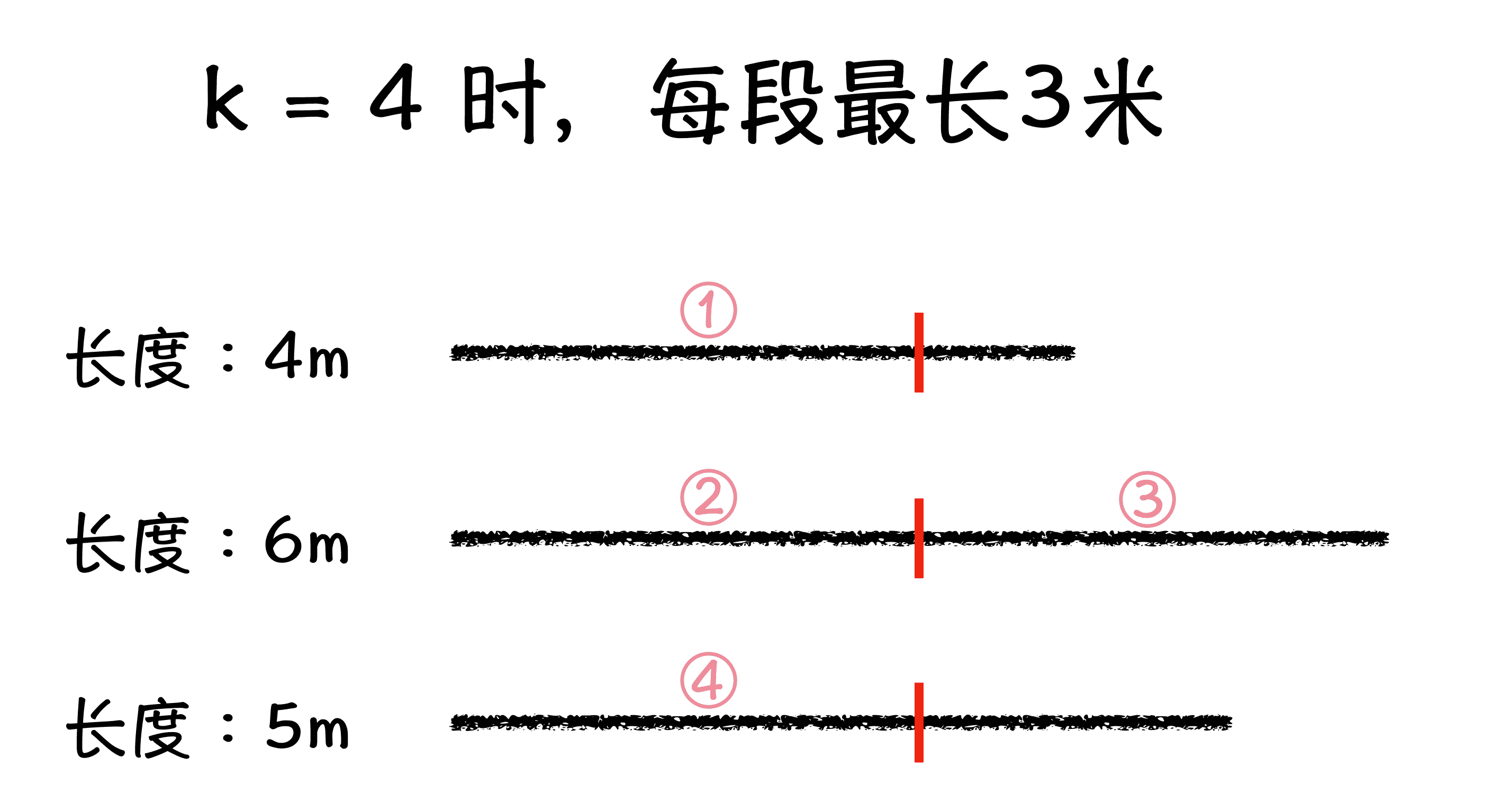
图 1:切绳子任务示意图
如图所示,如果你手中有 3 条绳子,分别是 4 米、6 米 和 5 米,想要切出等长的 4 段,你会发现,每段最长就是 3 米。
那么我们是如何得到“每段最长就是 3 米”这个答案的呢?当然,你可以采用枚举法,就是先尝试能不能切出至少 4 段的 1 米长绳子,如果可以的话,再去尝试每段长度 2 米是否可行,依次尝试下去,直到尝试不下去为止。最后一次尝试可行的长度,就是每段绳子的最长长度了。
这种做法,就像前面故事中想要一本一本进行尝试的女生,显得低效且繁琐。而今天,我将扮演图书馆阿姨的角色,当然,不会像故事中的阿姨一样,犯了前提条件没有搞清的错误,去给你讲一种更高效的方法!
必知必会,查缺补漏
1. 二分查找算法基础
最简单的二分算法的形式,就是在一个有序数组中,查找一个数字 x 是否存在。而二分算法,就是要基于这种有序性,才能对原问题进行加速求解。
我们先来思考,如何在一个数组中查找一个数字 x,最直接的方法,就是从头到尾一个一个找,找到了就是有数字 x,找不到就是没有数字 x。
而二分算法呢,是确定一个查找区间,然后从查找区间的一半处,与 x 进行比较,如果中间的数字比 x 大,说明 x 在前半段,就把后半段扔掉;如果比 x 小,就把前半段扔掉,继续在后半段区间内查找。你会发现,二分查找的过程,每一次比较,都会使区间减少一半,对于一个大小为 n 的区间,我们只需要 log2n 次比较操作即可确定结果。
具体的过程呢,如下图所示:
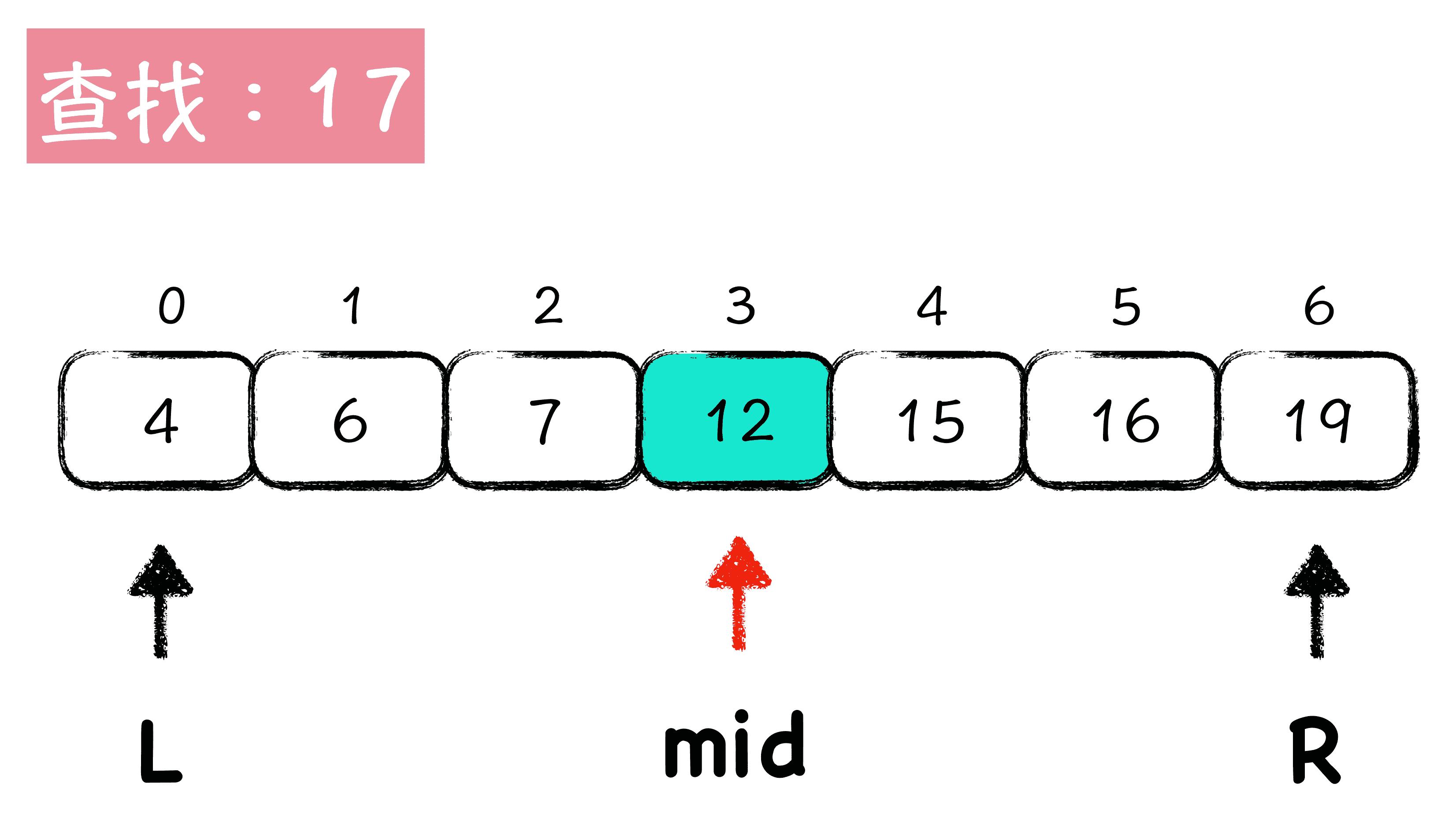
图 2:二分查找算法示意图
图中呢,我们以查找 17 这个数字为例,L 和 R 所圈定的,就是当前的查找区间,一开始 L = 0,R = 6,mid 所指向的就是数组的中间位置,根据 L 和 R 计算得到 mid 的值是 3。查看数组第 3 位的值是 12,比待查找值 17 要小,说明如果 17 在这个有序数组中,那它一定在 mid 所指向位置的后面,而 mid 本身所指向的数字已经确定不是 17 了,所以下一次我们可以将查找区间,定位到 mid + 1 到 R,也就是将 L 调整到 mid + 1(即数组第 4 位)的位置。
理解二分查找的过程,首先要理解二分查找是怎么保证查找过程正确性的。中心思想就一个:不管如何调整区间,都要保证待查找数字,总是落在我们的由 L 和 R 标记的查找区间内部。而二分查找,实际上“二分”的就是查找范围。这个过程,就像警察排查犯罪嫌疑人一样,通过一些特定的条件,快速地缩小范围,并锁定真正的罪犯。
下面是一份二分查找的示例代码:
int binary_search(int *arr, int n, int x) {
int l = 0, r = n - 1, mid;
while (l <= r) {
mid = (l + r) » 1;
if (arr[mid] == x) return mid;
if (arr[mid] > x) r = mid - 1;
else l = mid + 1;
}
return -1;
}
如代码所示,binary_search 函数传入三个参数,分别代表有序数组 arr,数组长度 n 和待查找数字 x。如果在数组中存在数字 x,函数将返回 x 数字的下标,否则就会返回 -1,代表数组中不存在数字 x。
你会看到,函数中有一个 while 循环,循环的执行条件是 l <= r,意味着待查找区间不为空。每次循环开始的时候,都是先通过 l 和 r 的值,计算得到一个中间位置的下标 mid 值,然后比较 mid 位置的值与 x 的大小关系,从而确定区间调整策略。
如果 arr[mid] 大于 x,说明 x 值在区间的前半段,那么 mid 及 mid 位置以后的值,就不在下一次查找的范围之内了,我们就把区间的尾部位置 r 向前移动,移动到 mid - 1 位。arr[mid] 小于 x 时候的调整策略与之类似。
至此,我们就学习完了基础的二分查找算法。
2. 二分答案的基本思路
其实二分查找的算法思想,最有价值的部分,不是刚才讲的有序数组查找问题。而是由其衍生出来的叫做“二分答案”的思想。
关于二分答案的思想,你可以先回想一下,我们是如何介绍数组与函数的关系的?我们说:数组和函数本质上做的都是映射,函数是压缩的数组,数组是展开的函数。
我们沿着函数和数组的关系,回头再看看二分查找的代码,你会发现二分查找是在一个有序数组中,确定某一位为待查找值的位置,也就是 arr[x] = y,给定待查找 y 值,确定 x 值。对于这个有序数组,我们可以看成是一个单调函数,而对于这个 arr[x] = y 中去确定 x 值的过程,可以看成是对单调函数 f(x) = y 进行求解的过程。
如何判断,什么场景下需要使用二分思想对问题求解呢?其实,二分能解决的问题,还是比较有代表性的,基本需要满足如下两点:
- f(x) 是一个单调函数。
- f(x) = y 函数,由 x 确定 y 值比较简单,而由 y 值确定 x 就比较困难。
关于第一点,我就不做过多解释了。至于第二点,你可以参考有序数组那个例子,对于数组来说,arr[x] = y,给定数组下标 x,确定值 y,这个过程对于计算机来说很容易,可给定 y 值,确定 y 值所在的下标 x,这个过程就不太容易了。所以,我们使用了二分查找算法。
总地来说,二分答案就是把二分查找过程中的数组换成了函数。关于二分答案的知识,你先理解思想,接下来我会用具体例子来给你展示。
一起动手,搞事情
今天给你留的作业题呢,是一个我们大家普遍都比较关心的问题,与计算工资有关系。下表是“个人所得税缴纳税率表”的一部分:

按照表格所示,如果一个人的每月工资是 18600,首先扣除不超过 3000 部分的 3% 的所得税 90 元,然后扣除 3000 到 12000 部分的 10%,就是 (12000 - 3000) * 10% = 900,最后是扣除 12000 到 18600 的部分的 20%,也就是 (18600 - 12000) * 20% = 1320。所以,此人每月到手工资应该是:18600 - 90 - 900 - 1320 = 16290 元。
如果要是让你通过上表,计算一个人的税后工资,那这个任务可太容易了,我不会将这么简单的任务交给你的。
你今天要做的,是通过一个人的税后工资,反推出他 / 她的税前工资,也就是针对于上面这个例子,我给出税后工资 16290,你的程序应该能够计算得到税前工资 18600。想一想,怎么做吧,加油!
切出最长的绳子
最后,我们回到今天的任务。我们将每一段绳子的长度 x,与能切出来的绳子段数之间,看成一个映射关系,用函数 f(x) = y 来表示,代表每一段长度为 x 的情况下,最多能切出来 y 段绳子。你很容易发现,f 函数是一个单调函数,随着每一段长度的增加,能切出来的段数 y 是在减少的,而对于我们来说,就是要确定 y = k 时的 x 的最大值。
让我们总结以下 f(x) 函数的性质,首先 f(x) 函数是单调函数,x 越大,y 值越小。其次,你应该可以感受出来,当我给你每一段长度 x 的时候,你很容易确定 f(x) = y 的 y 值,而如果让你通过 y 值求解 x,就没那么容易了!
至此,我们从这个任务出现的问题中,看到了能够使用二分思想的两个最重要的性质,下面我们就用二分思想的思路,来解决这个问题,下面是我给出的参考代码:
#define EPS 1e-7
double l[100], n;
int f(double x) {
int cnt = 0;
for (int i = 0; i < n; i++) {
cnt += (int)floor(l[i] / x);
}
return cnt;
}
double binary_search(double *l, double *r, int k) {
if (r - l <= EPS) return r;
double mid = (l + r) / 2.0;
if (f(mid) < k) return bs(l, mid, k);
return bs(mid, r, k);
}
代码中的 binary_search 就是二分答案的过程,函数 f 传入每一段的长度 x,返回最多能切多少段,变量 n 记录的是原始绳子的数量,l 数组记录的是每一段原始绳子的长度。
让我们把目光集中到 binary_search 函数过程,这一段二分答案的程序,使用递归的程序设计技巧,其实和之前给你演示的循环程序本质思想都是一样的。其中 l 和 r 表示待查找区间范围,也就是每一段绳子的长度范围。
递归程序的边界条件,是当 r - l 小于等于一个极小值的时候,就终止递归。这里需要特殊的说明一下,根据浮点数在我们计算机中的表示方法,我们很难用判等操作来判断两个浮点值相等,取而代之的,就是当这两个浮点值已经很接近的时候,我们就认为它俩是一个值。代码中的 EPS 是一个宏,就是我们控制的精度,一般控制在 10−7 范围,两个值相差不到 10−7 的时候,我们就认为这两个浮点值相等。
关于调整搜索范围的代码,我就不再赘述了,剩下的你自己就可以看明白了。至此,我们就解决了今天的任务。
课程小结
最后,我们来做一下课程小结。今天我们学习了二分查找算法,以及由二分思想延伸出来的二分答案相关算法思想。关于这些知识,你只需要记住如下几点即可:
- 二分算法框架,是求解具有单调性问题的利器。
- 二分算法,通常用来求解那些 f(x) = y 问题中,给定 y,求解 x 的问题。
- 再次强调,数组和函数在思维层面,没有什么本质差别。
总结完了以后呢,我们再回顾那个笑话故事,图书馆阿姨用二分算法为什么会导致图书馆丢了 39 本书呢?如果我们将书的编号和是否是图书馆的书之间,做一个函数映射的话,你会发现这种映射出来的函数,本质上没有单调性。所以,原因就是阿姨将二分算法思想用错场景了。
好了,今天就到这里了,我是胡光,我们下期见。
文章作者 anonymous
上次更新 2024-05-18