39_强化学习在自然语言处理下的应用篇
文章目录
强化学习在自然语言处理下的应用篇
来自: AiGC面试宝典
• 强化学习在自然语言处理下的应用篇
• 一、强化学习基础面
• 1.1 介绍一下强化学习?
• 1.2 介绍一下强化学习 的 状态(States) 和 观测(Observations)?
• 1.3 强化学习 有哪些 动作空间(Action Spaces),他们之间的区别是什么?
• 1.4 强化学习 有哪些 Policy策略?
• 1.5 介绍一下 强化学习 的 轨迹?
• 1.6 介绍一下 强化学习 的 奖赏函数?
• 1.7 介绍一下 强化学习问题?
二、 RL发展路径(至PPO)
• 2.1 介绍一下 强化学习 中 优化方法 Value-based?• 2.2 介绍一下 强化学习 中 贝尔曼方程?• 2.3 介绍一下 强化学习 中 优势函数Advantage Functions?
• 致谢
一、强化学习基础面
1.1 介绍一下强化学习?
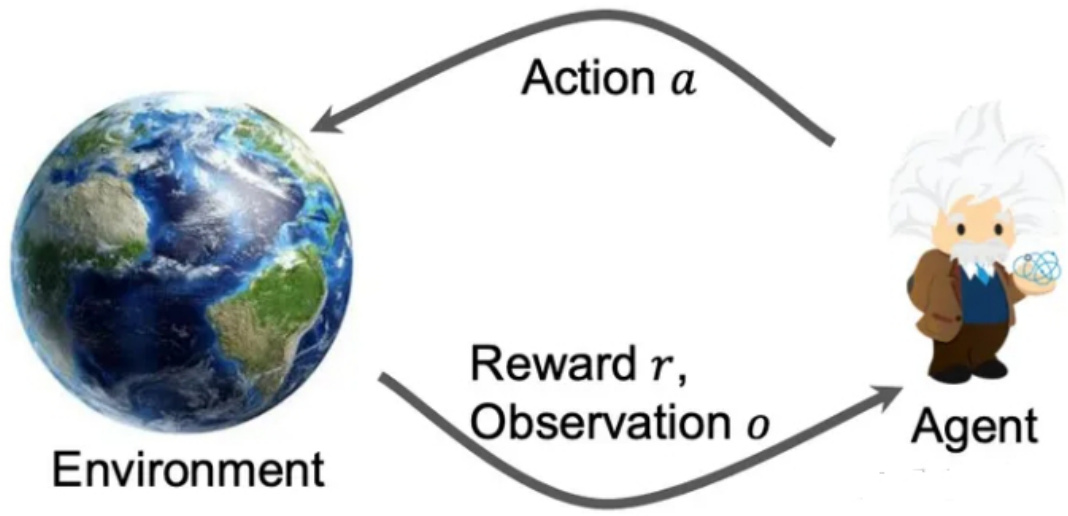
强化学习(Reinforcement Learning)是一种时序决策学习框架,通过智能体和环境交互
$$ a_{t}=\pi(o_{t}) $$
得到的奖励
$$ r_{t}=r(o_{t},a_{t}) $$
从而来优化策略 π,使其能够在环境中自主学习。
1.2 介绍一下强化学习 的 状态(States) 和 观测(Observations)?
• 状态(States):对于世界状态的完整描述
• 观测(Observations):对于一个状态的部分描述,可能会缺失一些信息。当O $|=,$ S时,称O为完美信息/fullyobserved; $\mathsf{O}\mathsf{<}$ <S时,称O为非完美信息/partially observed。
1.3 强化学习 有哪些 动作空间(Action Spaces),他们之间的区别是什么?
• 离散动作空间:当智能体只能采取有限的动作,如下棋/文本生成• 连续动作空间:当智能体的动作是实数向量,如机械臂转动角度其区别会影响policy网络的实现方式。
1.4 强化学习 有哪些 Policy策略?
• 确定性策略Deterministic Policy: at $\mathbf{\mu}=\mathfrak{u}({\mathsf{s t}})$ ,连续动作空间• 随机性策略Stochastic Policy: at ~ π(·|st) ,离散动作空间
1.5 介绍一下 强化学习 的 轨迹?
• 轨迹:指的是状态和行动的序列
$$ {\boldsymbol{\tau}}=\left(\ensuremath{\boldsymbol{s}}{0},\ensuremath{\boldsymbol{a}}{0},\ensuremath{\boldsymbol{s}}{1},\ensuremath{\boldsymbol{a}}{1},\dots\right) $$
- 状态转换函数(transition function):
$$ s_{t+1}\sim P(\cdot|s_{t},a_{t}) $$
- 初始状态是从初始状态分布中采样的,一般表示为
$$ s_{0}\sim\rho(\cdot) $$
1.6 介绍一下 强化学习 的 奖赏函数?
$$ r_{t}\sim R\left(s_{t},a_{t},s_{t+1}\right)/r_{t}\sim R\left(s_{t},a_{t}\right) $$
智能体的目标是最大化行动轨迹的累计奖励:
$$ R(\bar{\tau})=\sum_{t=0}^{\infty}\gamma^{t}r_{t} $$
1.7 介绍一下 强化学习问题?
• 核心问题:选择一种策略从而最大化预期收益
- 假设环境转换和策略都是随机的,则T步行动轨迹概率:
$$ \begin{array}{r}{P(\tau\mid\pi)=\rho_{0}\left(s_{0}\right)\prod_{t=0}^{T-1}P\left(s_{t+1}\mid s_{t},a_{t}\right)\pi\left(a_{t}\mid s_{t}\right)}\ {\sum\dots,\rho_{s}\left(s_{t},s_{t}\right)}\end{array} $$
- 预期收益:
$$ \begin{array}{r}{J(\pi)=\int_{\tau}\dot{P(\tau\mid\pi)}R(\tau)=\underset{\tau\sim\pi}{\mathrm{E}}\left[R(\tau)\right]}\end{array} $$
- 核心优化问题:找到最优策略
$$ \begin{array}{r}{\stackrel{?}{{\pi}^{}}=\arg\operatorname{max}_{\pi}J(\pi)}\end{array} $$
二、RL发展路径(至PPO)

2.1 介绍一下 强化学习 中 优化方法 Value-based?
• value-based:状态的值 V(s) 或者 状态行动对(state-action pair) 的值Q(s,a) ,作为一种累积奖赏的估计,可以通过最大化值函数来优化得到最优策略
- 最优值函数(Optimal Value Function):
$$
V^{*}(s)=\mathrm{max}{\pi}\mathrm{E}[R(\tau)\mid s{0}=s]
$$
- 最优动作-值函数(Optimal Action-Value Function):
$$ \begin{array}{r l}&{Q^{}\left(s,a\right)=}\ &{\operatorname{max}{\pi}\underset{\tau\sim\pi}{\mathrm{E}}\left[R(\tau)\mid s{0}=s,a_{0}=a\right]}\end{array} $$
最优动作:
$$ a^{}\left(s\right)=\arg\operatorname{max}_{a}Q^{*}\left(s,a\right) $$
- 两者的关系:
$$ V^{\pi}(s)=\operatorname{E}{a\sim\pi}\left[Q^{\pi}(s,a)\right];V^{}(s)=\operatorname{max}{a}Q^{*}(s,a) $$
2.2 介绍一下 强化学习 中 贝尔曼方程?
• 中心思想:当前值估计 $\because$ 当前奖赏 $^+$ 未来值估计
$$ \begin{array}{r l}&{\quad V^{\pi}(s)=\underset{a\sim\mathcal{T}^{n}}{\mathrm{E}}\left[r(s,a)+\gamma V^{\pi}\left(s^{\prime}\right)\right]}\ &{\quad\quad\quad\quad\quad\quad\quad\quad}\ &{Q^{\pi}(s,a)=\underset{s^{\prime}\sim P}{\mathrm{E}}\left[r(s,a)+\gamma\underset{a^{\prime}\sim\pi}{\mathrm{E}}\left[Q^{\pi}\left(s^{\prime},a^{\prime}\right)\right]\right]}\end{array} $$
所以,最优值函数的贝尔曼公式为:
$$
\begin{array}{c}{{V^{\ast}(s)=\underset{a}{\mathrm{max}}\mathrm{\boldmath{E}}_{s^{\prime}\sim P}[r(s,a)+\gamma V^{\ast}\left(s^{\prime}\right)]}}\ {{Q^{\ast}\left(s,a\right)=\underset{s^{\prime}\sim P}{\mathrm{E}}\left[r(s,a)+\gamma\underset{a^{\prime}}{\mathrm{max}}Q^{\ast}\left(s^{\prime},a^{\prime}\right)\right]}}\end{array}
$$
2.3 介绍一下 强化学习 中 优势函数Advantage Functions?
强化学习中,有时不需要知道一个行动的绝对好坏,而只需要知道它相对于其他action的相对优势。即
$$ A^{\pi}(s,a)=Q^{\pi}(s,a)-V^{\pi}(s) $$
文章作者 大模型
上次更新 2025-03-09