45_图解分布式训练_一_流水线并行_Pipeline_Parallelism
文章目录
图解分布式训练(一) —— 流水线并行(Pipeline Parallelism)
来自: AiGC面试宝典
为什么需要流水线并行(Pipeline Parallelism)?
回顾ChatGPT的发展历程,我们可以总结出大语言模型(LLM)取得惊艳效果的要点(重要性从高到低排序):
- 愿意烧钱,且接受“烧钱 != 好模型”的现实
- 高质量的训练语料
- 高效的分布式训练框架和充沛优质的硬件资源
- 算法的迭代创新
在大模型训练这个系列里,我们将一起探索学习几种经典的分布式并行范式,包括流水线并行(PipelineParallelism),数据并行(Data Parallelism)和张量并行(Tensor Parallesim)。微软开源的分布式训练框DeepSpeed,融合了这三种并行范式,开发出3D并行的框架,实现了千亿级别模型参数的训练。
本篇文章将探索流水线并行,经典的流水线并行范式有Google推出的Gpipe,和微软推出的PipeDream。两者的推出时间都在2019年左右,大体设计框架一致。主要差别为:在梯度更新上,Gpipe是同步的,PipeDream是异步的。异步方法更进一步降低了GPU的空转时间比。虽然PipeDream设计更精妙些,但是Gpipe因为其“够用”和浅显易懂,更受大众欢迎(torch的pp接口就基于Gpipe)。因此本文以Gpipe作为流水线并行的范例进行介绍。
本文内容包括:
- 优化目标
- 模型并行
- 流水线并行a. 切分micro-batchb. Re-materialization (active checkpoint)
- 实验效果a. GPU数量 VS 模型大小b. GPU数量 VS 训练速度c. Gpipe下单GPU的时间消耗分析
一、流水线并行(Pipeline Parallelism) 优化目标是什么?
当你从单卡穷人变成多卡富翁时,你做分布式训练的总体目标是什么呢?(虽然手握一张A100怎么能是穷呢)
• 能训练更大的模型。理想状况下,模型的大小和GPU的数量成线性关系。即GPU量提升x倍,模型大小也能提升x倍。
• 能更快地训练模型。理想状况下,训练的速度和GPU的数量成线性关系。即GPU量提升x倍,训练速度也能提升x倍。
这是目标,也是难点,难在于:
• 训练更大的模型时,每块GPU里不仅要存模型参数,还要存中间结果(用来做Backward)。而更大的模型意味着需要更多的训练数据,进一步提高了中间结果的大小。加重了每块GPU的内存压力。我们将在下文详细分析这一点。(对应着GPU中的内存限制)
• 网络通讯开销。数据在卡之间进行传输,是需要通讯时间的。不做设计的话,这个通讯时间可能会抹平多卡本身带来的训练速度提升。(对应着GPU间的带宽限制)
• 明确这两个训练目标后,我们来看并行范式的设计者,是如何在现有硬件限制的条件下,完成这两个目标
的。
二、图解 流水线并行(Pipeline Parallelism)模型并行 必要性?
• 动机:当你有一个单卡装不下的大模型时• 解决办法:把模型隔成不同的层,每一层都放到一块GPU上,如下图:
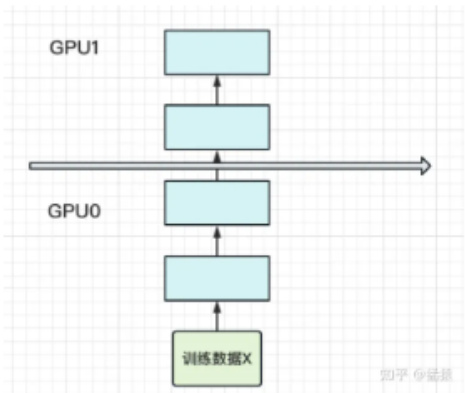
此时,模型做一轮forward和backward的过程如下:
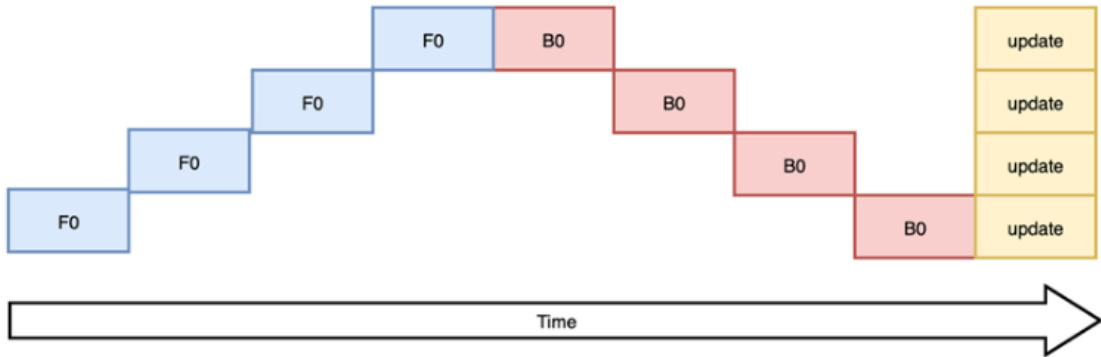
其中下标表示batch编号,这里只有一个batch,因此下标都是0。每一行表示一个GPU。每一列表示timestep。这张图的含义是:我在GPU0上做完一次forward,然后将GPU0上最后一层的输入传给GPU1,继续做forward,直到四块GPU都做完forward后,我再依次做backward。等把四块GPU上的backward全部做完后,最后一个时刻我统一更新每一层的梯度。
这样做确实能训更大的模型了,但也带来了两个问题:
1. GPU利用度不够
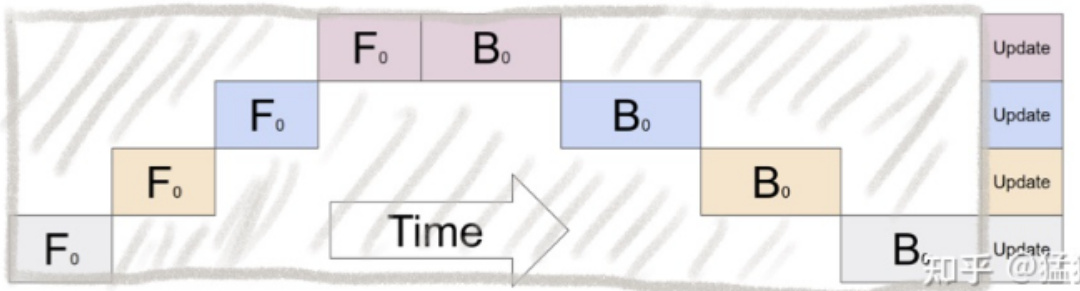
如图,阴影部分所表示的时间段里,总有GPU在空转。在Gpipe中,将阴影部分定义为bubble。我们来计算一下bubble。假设有 K 块GPU,而单块GPU上做一次forward和backward的时间为:
$$ t_{f b}=(t_{f}+t_{b}) $$
那么:
• 图中灰色长方形的整体面积为:
$$ K*K t_{f b}(\rightleftarrows=K,\mathrel{\stackrel{\leftarrow}{\lnot\lnot}}K=K t_{f b}) $$
• 图中实际在做forward和backward的面积为:
$$ K t_{f b} $$
• 图中阴影部分的面积为:
$$ K*K t_{f b}-K t_{f b}=(K-1)K t_{f b} $$
• 图像阴影部分的占比为:
$$ (K-1)K t_{f b}/K K t_{f b}=(K-1)/K $$
则我们定义出bubble部分的时间复杂度为:
$$ \begin{array}{r}{O(\frac{K-1}{K})}\end{array} $$
当K越大,即GPU的数量越多时,空置的比例接近1,即GPU的资源都被浪费掉了。因此这个问题肯定需要解决。
- 中间结果占据大量内存
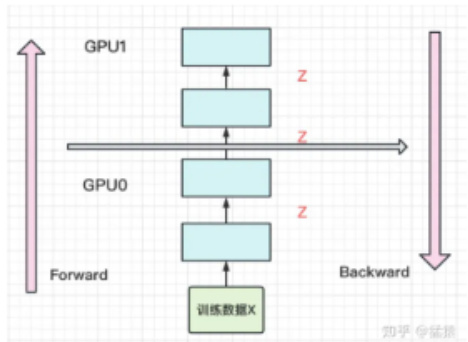
在做backward计算梯度的过程中,我们需要用到每一层的中间结果z。假设我们的模型有L层,每一层的宽度为d,则对于每块GPU,不考虑其参数本身的存储,额外的空间复杂度为
$$ O(N*\frac{L}{K}*d) $$
从这个复杂度可以看出,随着模型的增大,N,L,d三者的增加可能会平滑掉K增加带来的GPU内存收益。因此,这也是需要优化的地方。
三、流水线并行(Pipeline Parallelism) 图解?
朴素的模型并行存在GPU利用度不足,中间结果消耗内存大的问题。
而Gpipe提出的流水线并行,就是用来解决这两个主要问题的。
3.1 切分micro-batch
• 核心思想:在模型并行的基础上,进一步引入数据并行的办法,即把原先的数据再划分成若干个batch,送入GPU进行训练。未划分前的数据,叫mini-batch。在mini-batch上再划分的数据,叫micro-batch。图例如下:

其中,第一个下标表示GPU编号,第二个下标表示micro-batch编号。假设我们将mini-batch划分为M个,则流水线并行下,bubble的时间复杂度为:
$$ \begin{array}{r}{O(\frac{K-1}{K+M-1})}\end{array} $$
注: (推导过程略,可参照第二部分的bubble推导流程)
Gpipe通过实验证明,当 $M>=4K$ 时,bubble产生的空转时间占比对最终训练时长影响是微小的,可以忽略不计。
将batch切好,并逐一送入GPU的过程,就像一个流水生产线一样(类似于CPU里的流水线),因此也被称为Pipeline Parallelism。
3.2 re-materialization(active checkpoint)
• 动机:虽然 切分micro-batch方法 能够 解决了GPU的空置问题,提升了GPU计算的整体效率。但是 如何解决 GPU的内存问题 呢?前文说过,随着模型的增加,每块GPU中存储的中间结果也会越大。• 核心方法:Gpipe采用了一种非常简单粗暴但有效的办法:用时间换空间,在论文里,这种方法被命名为re-materalization,后人也称其为active checkpoint。
具体来说,就是几乎不存中间结果,等到backward的时候,再重新算一遍forward,图例如下:
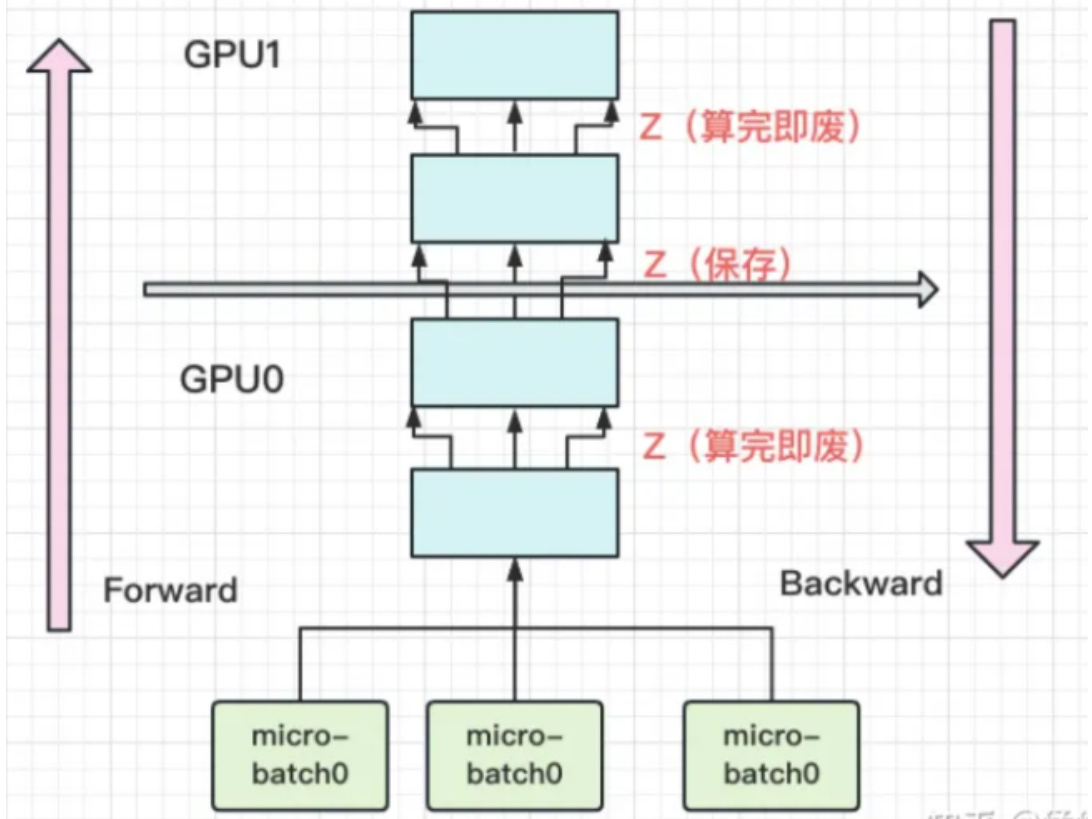
每块GPU上,我们只保存来自上一块的最后一层输入z,其余的中间结果我们算完就废。等到backward的时候再由保存下来的z重新进行forward来算出。
现在我们来计算每块GPU峰值时刻的内存:
每块GPU峰值时刻存储大小 $=$ 每块GPU上的输入数据大小 $^+$ 每块GPU在forward过程中的中间结果大小每块GPU上固定需要保存它的起始输入,我们记起始输入为 N (即mini-batch的大小)。
每个micro-batch是流水线形式进来的,算完一个micro-batch才算下一个。在计算一个micro-batch的过程中,我们会产生中间变量,它的大小为
$$ \frac{N}{M}*\frac{L}{K}*d $$
注:(其中M为micro-batch个数)因此,每块GPU峰值时刻的空间复杂度为
$$ \begin{array}{r}{O(N+\frac{N}{M}*\frac{L}{K}*d)}\end{array} $$
与朴素模型并行中的GPU空间复杂度
$$ \begin{array}{r}{\mathopen:O\mathopen{}\mathclose\bgroup\left(N*\frac{\tilde{L_{r}}}{K}*d\aftergroup\egroup\right)^{-}}\end{array} $$
相比,可以发现,由于采用了micro-batch的方法,当L变大时,流水线并行相比于朴素模型并行,对GPU内存的压力显著减小。
如果你使用Pytorch提供的pipeline接口,其中有一个参数叫checkpoint,就是用来做这一项的。
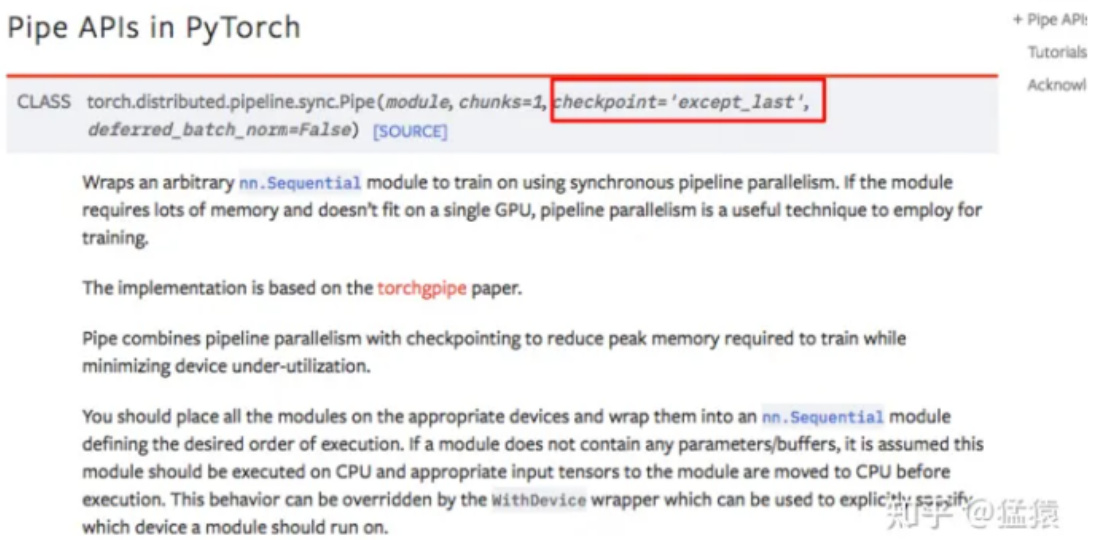
最后,再提一点,在micro-batch的划分下,我们在计算Batch Normalization时会有影响。Gpipe的方法是,在训练时计算和运用的是micro-batch里的均值和方差,但同时持续追踪全部mini-batch的移动平均和方差,以便在测试阶段进行使用。Layer Normalization则不受影响。
四、流水线并行(Pipeline Parallelism)优缺点?
回顾第二部分的两个目标,Gpipe真的实现了吗?如果实现不了,又是因为什么原因呢?我们来看下实验效果。
4.1 GPU数量 VS 模型大小
| NVIDIAGPUs(8GBeach) | Naive-1 | Pipeline-1 | Pipeline-2 | Pipeline-4 | Pipeline-8 |
| AmoebaNet-D(L,D) | (18,208) | (18,416) | (18,544) | (36,544) | (72,512) |
| #ofModelParameters | 82M | 318M | 542M | 1.05B | 1.8B |
| TotalModelParameterMemory | 1.05GB | 3.8GB | 6.45GB | 12.53GB | 24.62GB |
| PeakActivationMemory | 6.26GB | 3.46GB | 8.11GB | 15.21GB | 26.24GB |
| CloudTPUv3(16GBeach) | Naive-1 | Pipeline-1 | Pipeline-8 | Pipeline-32 | Pipeline-128 |
| Transformer-L | 3 | 13 | 103 | 415 | 1663 |
| #ofModelParameters | 282.2M | 785.8M | 5.3B | 21.0B | 83.9B |
| TotalModelParameterMemory | 11.7G | 8.8G | 59.5G | 235.1G | 937.9G |
| PeakActivationMemory | 3.15G | 6.4G | 50.9G | 199.9G | 知手96Q0孟猴 |
Gpipe分别在AmoebaNet(图像)和Transformer(自然语言)两个大模型上做了实验。
• Naive表示单卡• Pipeline-N表示re-materalization $+\mathsf{N}$ 卡。• AmeobaNet-D和Trasformer-L一行表示超参数的量
of Model Parameter表示模型的参数量
• Total Model Parameter Memory表示模型参数所占内存大小• Peak Activation Memory表示峰值时中间结果大小。可以发现,中间结果占据的内存大小是相当可观的。
从实验结果里,我们可以发现:
• 在Transformer上,Gpipe基本实现了模型大小(参数量)和GPU个数之间的线性关系。例如从32卡增到128卡时,模型的大小也从21.08B增加到82.9B,约扩4倍• 对AmoebaNet而言,却没有完全实现线性增长。例如从4卡到8卡,模型大小从1.05B到1.8B,不满足2倍的关系。本质原因是AmoebaNet模型在切割时,没有办法像Transformer一样切得匀称,保证每一块GPU上的内存使用率是差不多的。因此对于AmoebaNet,当GPU个数上升时,某一块GPU可能成为木桶的短板。-
4.2 GPU数量 VS 训练速度
4.2.1 关掉NVlinks
为了验证Gpipe框架带来的收益,实验中关掉了NVlinks(GPU间快速通信的桥梁。估计是通过强迫GPU先连CPU然后再连别的GPU做到的)。关掉的意义在于说明,不靠硬件本身的高效通讯带来的收益,Gpipe一样能做的很好。实验效果如下:
| GPU | AmoebaNet | Transformer | ||||
| K= | 2 | 4 | 8 | 2 | 4 | 8 |
| M = 32 | 1 | 1.7 | 2.7 | 1 | 1.8 | 3.3 |
${\tt M}{=}32$ 表示micro-batch的数量为32,K表示GPU数量。从实验结果可知,在关掉NVlinks的情况下,Gpipe一样也能实现随着GPU数量的增加,训练速度也增加的效果。虽然这两者间不是线性的。同样,因为模型切割不均的原因,AmoebaNet的表现不如Transformer。
4.2.2 开启NVlinks,并寻找最佳M
| TPU | AmoebaNet | Transformer | ||||
| K= | 2 | 4 | 8 | 2 | 4 | 8 |
| M =1 | 1 | 1.13 | 1.38 | 1 | 1.07 | 1.3 |
| M = 4 | 1.07 | 1.26 | 1.72 | 1.7 | 3.2 | 4.8 |
| M =32 | 1.21 | 1.84 | 3.48 | 1.8 | 3.4 | 6.3 |
当重新开启NVlinks后,我们来看M的大小(即流水线的核心)对训练速度的影响。
• 当M $|=1$ 1的时候,如前文所说,GPU的空置率太高,因此两个模型都没有实现训练速度和GPU个数间的线性关系
• 当M=4时,表现明显好转。
• 当M $_{1=32}$ 时,表现最佳,且Transformer基本实现了训练速度和GPU个数的线性关系。
4.2.3 Gpipe下时间消耗分布
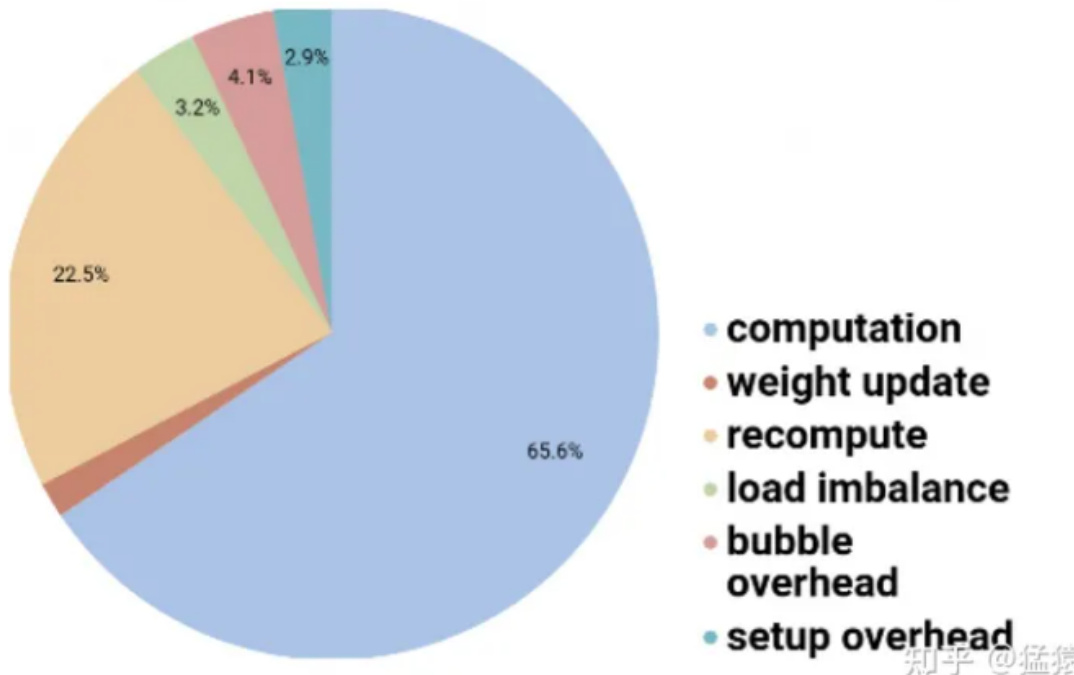
• 对每块GPU来说,约2/3的时间,是真正花在计算上的。
• 其余1/3的时间,大部分花在re-materalization策略下的重计算上。因为采用流水线的方法,bubble的时间也被压缩到很短,可以忽略不计。
文章作者 大模型
上次更新 2025-03-09