• LLMs 位置编码篇

• 动机• 一、什么是位置编码？• 二、为什么需要位置编码？• 三、什么是绝对位置编码？

• 3.1 训练式位置编码篇

• 3.1.1 什么是 训练式位置编码？
• 3.1.2 如何为每个位置的词向量注入位置信息呢？
• 3.1.3 训练式位置编码篇 应用场景？
• 3.1.4 训练式位置编码篇 存在哪些问题？

• 3.2 Sinusoidal位置编码篇• 3.2.1 什么是 Sinusoidal位置编码？• 3.2.2 Sinusoidal位置编码 有哪些优点？

• 四、什么是相对位置编码？

• 五、旋转位置编码 RoPE篇• 5.1 旋转位置编码 RoPE 思路是什么？• 5.2 推导一下 旋转位置编码 RoPE ？• 5.3 旋转位置编码 RoPE 有什么优点？• 5.4 旋转位置编码 RoPE 被哪些 LLMs 应用？

• 六、长度外推问题篇

• 6.1 什么是 长度外推问题？• 6.2 长度外推问题 的 解决方法 有哪些？

• 七、 ALiBi (Attention with Linear Biases)篇 • 7.1 ALiBi (Attention with Linear Biases) 思路是什么？ • 7.2 ALiBi (Attention with Linear Biases) 的偏置矩阵是什么？有什么作用？ • 7.3 ALiBi (Attention with Linear Biases) 有什么优点？ • 7.4 ALiBi (Attention with Linear Biases) 被哪些 LLMs 应用？

• 致谢

动机

由于计算资源限制，目前的大模型大多在较小的上下文长度中进行训练，在推理中，若超出预训练的长度，模型的性能将会显著降低。于是涌现出了许多基于RoPE的长度外推的工作，旨在让大模型能够在预训练长度之外，取得更好的效果。

一、什么是位置编码？

句子中不同词语之前的位置信息十分重要，但是self-attention框架无法直接利用位置信息，因此研究者提出了许多方法将位置信息编码到学习过程中。

1. 绝对位置编码方法：将位置信息直接加入到输入中；
2. 相对位置编码方法：研究者通过微调attention的结构，使它具有识别token位置信息的能力。

二、为什么需要位置编码？

众所周知，transformer模型之所以能够取得如此卓越的效果，其中的Attention机制功不可没，它的本质是计算输入序列中的每个token与整个序列的注意力权重。假设 qm 和 kn 分别表示词向量 q 位于位置 m 和词向量 $\mathsf{k}$ 位于位置 n ，在未添加位置信息的时候，

$$ q_{m}=q,k_{n}=k, $$

则两者的注意力权重计算如下:

$$ a_{m,n}=\frac{\exp\left(\frac{q_{m}^{\mathrm{T}}k_{n}}{\sqrt{d}}\right)}{\sum_{j=1}^{N}\exp\left(\frac{q_{m}^{\mathrm{T}}k_{j}}{\sqrt{d}}\right)} $$

我们会发现，在未加入位置信息的情况下，无论 q 和 k 所处的位置如何变化，它们之间的注意力权重 $\mathsf{a}(\mathsf{m},\mathsf{n})$ 均不会发生变化，也就是位置无关，这显然与我们的直觉不符。对于两个词向量，如果它们之间的距离较近，我们希望它们之间的的注意力权重更大，当距离较远时，注意力权重更小。

为了解决这个问题，我们需要为模型引入位置编码，让每个词向量都能够感知到它在输入序列中所处的位置信息。我们定义如下函数，该函数表示对词向量 q 注入位置信息 m ，得到 qm ：

$$ q_{m}=f(q,m) $$

则 qm 与 kn 之间的注意力权重可表示为：

$$ a_{m,n}=\frac{\exp\left(\frac{f(q,m)^{\mathrm{T}}f(k,n)}{\sqrt{d}}\right)}{\sum_{j=1}^{N}\exp\left(\frac{f(q,m)^{\mathrm{T}}f(k,j)}{\sqrt{d}}\right)} $$

三、什么是绝对位置编码？

绝对位置编码比较简单，研究者一般会将绝对位置信息加到输入中：在输入的第 k 个向量xk​中加入位置向量pk​得到 $|p k^{+}x k$ ​，其中 $p k$ ​仅与 k 相关。计算pk​的方法一般有两种：训练式位置编码与Sinusoidal位置编码。

3.1 训练式位置编码篇

3.1.1 什么是 训练式位置编码？

训练式位置编码，顾名思义就是每个位置的位置向量会随着模型一起训练。假设模型最大输入长度为512，向量维度为768，我们可初始化一个 ${}^{.512^{\star}768}$ 的位置编码矩阵，该矩阵将参与模型的训练，从而学习得到每个位置所对应的向量表示。

3.1.2 如何为每个位置的词向量注入位置信息呢？

答案是相加，如以下公式所示，其中 pm 表示第 m 个位置的位置向量：

$$ q_{m}=f(q,m)=q+p_{m} $$

3.1.3 训练式位置编码篇 应用场景？

训练式位置编码广泛应用于早期的transformer类型的模型，如BERT、GPT、ALBERT等。

3.1.4 训练式位置编码篇 存在哪些问题？

模型不具有长度外推性，因为位置编码矩阵的大小是预设的，若对其进行扩展，将会破坏模型在预训练阶段学习到的位置信息。例如将512768扩展为1024768，新拓展的512个位置向量缺乏训练，无法正确表示512~1023的位置信息。但早期大家对长文本输入的需求并不如现在迫切。

3.2 Sinusoidal位置编码篇

3.2.1 什么是 Sinusoidal位置编码？

Sinusoidal位置编码是谷歌在Transformer模型中提出的一种绝对位置编码，它的形式如下，其中 d表示词向量的维度，k 表示位置索引， 2i 和 $2\mathrm{i}+1$ 表示位置向量的分量索引，例如 $_{p k,2}$ i​和 $p k,2i+$ 1​分别表示位置 k 的位置向量的第 2i 和第 $2\mathrm{i}+1$ 个分量：

$$ \left{\begin{array}{l l}{p_{k,2i}=\sin\Big(k/10000^{2i/d}\Big)}\ {p_{k,2i+1}=\cos\Big(k/10000^{2i/d}\Big)}\end{array}\right. $$

3.2.2 Sinusoidal位置编码 有哪些优点？

1. 周期性

Sinusoidal位置编码的每个分量都是正弦或余弦函数，所有每个分量的数值都具有周期性。如下图所示，每个分量都具有周期性，并且越靠后的分量，波长越长，频率越低。

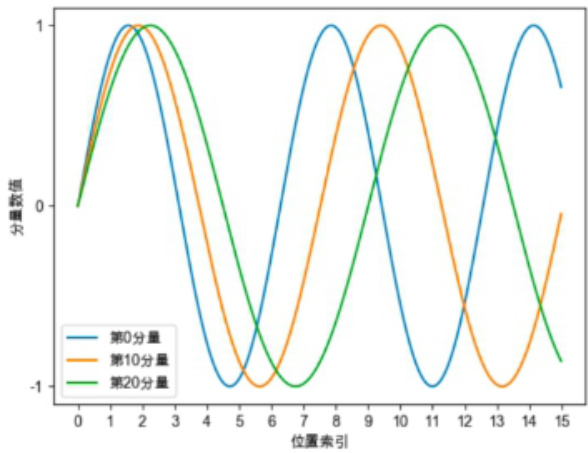
1. 远程衰减性

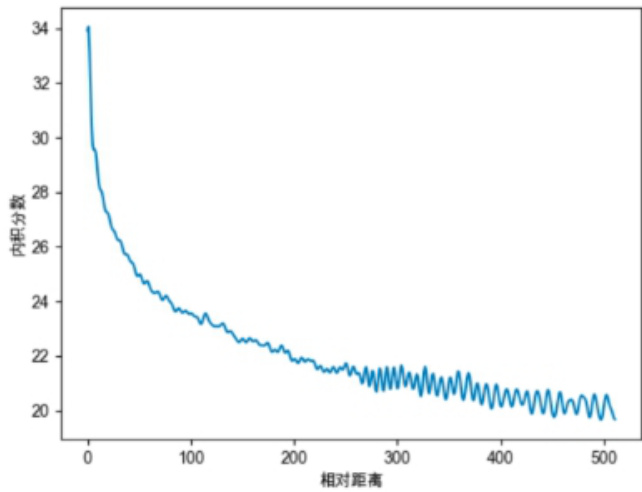
Sinusoidal位置编码还具有远程衰减的性质，具体表现为：对于两个相同的词向量，如果它们之间的距离越近，则他们的内积分数越高，反之则越低。如下图所示，我们随机初始化两个向量 q 和

k，将 q 固定在位置0上，k 的位置从 0 开始逐步变大，依次计算 q 和 k 之间的内积。我们发现随着 q 和 k 的相对距离的增加，它们之间的内积分数震荡衰减。

四、什么是相对位置编码？

前面讲到相对位置编码是微调Attention矩阵的计算方式，先看看绝对位置编码怎样计算Attention矩阵：

$$ \begin{array}{r l}&{q_{m}=W_{q}(x_{m}+p_{m})}\ &{k_{n}=W_{k}(x_{n}+p_{n})}\ &{q_{m}^{T}k_{n}=x_{m}^{T}W_{q}^{T}W_{k}x_{n}+x_{m}^{T}W_{q}^{T}W_{k}p_{n}+p_{m}^{T}W_{q}^{T}W_{k}x_{n}+p_{m}^{T}W_{q}^{T}W_{k}p_{n}}\end{array} $$

可以看到计算attention矩阵的过程如公式(1)所示，其中第一项和位置信息无关，第二至四项和位置信息相关。因此研究者通常是直接修改第二至四项的内容，直接在attention矩阵中添加相对位置信息。常见的有以下几种方法：

XLNET式：如(2)所示，xlnet将(1)中的二至四项都做了改变，具体的将pn​替换为了Sinusoidal生成式编码 $R n{-}m$ ​，将pm​换成了两个可以训练的向量 $u,v_{\circ}$ 。

$q_{m}^{T}k_{n}=x_{m}^{T}W_{q}^{T}W_{k}x_{n}+x_{m}^{T}W_{q}^{T}\tilde{W}{k}\tilde{R}{n-m}+u^{T}W_{q}^{T}W_{k}x_{n}+v^{T}W_{q}^{T}\tilde{W}{k}\tilde{R}{n-m}(2)$

T5式：如(3)所示，它的作者认为输入和位置间不应过多的交互，因此将第二、三项删除，将第四项都替换为一个可学习的偏执bm,n​，这仅仅是在Attention矩阵的基础上加一个可训练的偏置项而已，十分简单。

$$ q_{m}^{T}k_{n}=x_{m}^{T}W_{q}^{T}W_{k}x_{n}+b_{m,n} $$

DeBerta式：和T5的构造相反，它舍弃了公式(1)中第四项，保留了第二、三项并将位置信息替换为了相对位置向量

$$ q_{m}^{T}k_{n}=x_{m}^{T}W_{q}^{T}W_{k}x_{n}+x_{m}^{T}W_{q}^{T}W_{k}\tilde{R}{n-m}+\tilde{R}{n-m}^{T}W_{q}^{T}W_{k}x_{n} $$

五、旋转位置编码 RoPE篇

5.1 旋转位置编码 RoPE 思路是什么？

作用在每个 transformer 层的 self-attention 块，在计算完 Q/K 之后，旋转位置编码作用在 Q/K上，再计算attention score。

5.2 推导一下 旋转位置编码 RoPE ？

Attention的核心运算是内积，所以我们希望经过内积的结果能够带有相对信息。那么我们希望qm和kn的内积仅与输入xm,xn和他们的相对位置m-n有关，那么我们可以假设存在函数g，使得：

$$ \begin{array}{r l r}{q_{m}^{T}k_{n}}&{{}=}&{g(x_{m},x_{n},m-n)}\end{array} $$

为了方便理解我们可以先考虑二维形式，然后借助复数的运算法则来理解。首先分别用复数的指数形式表示各个向量变化,即有：

$$ \begin{array}{r l}&{q_{m}=(W_{q}x_{m})e^{i m\theta}}\ &{k_{n}=(W_{k}x_{n})e^{i n\theta}}\ &{q_{m}^{T}k_{n}=R e[(W_{q}x_{m})(W_{k}x_{n})^{*}e^{i(m-n)\theta}]}\end{array} $$

PS1. 向量内积与复数乘积的关系为内积 ，其中 Re 表示复数的实部。PS2. 这个形式证明过程可以参考论文的3.4.1节。但是要注意的是向量内积是标量，而$g(x_{m},x_{n},m-n)\mid_{\ast}^{1}$ 是向量，所以其公式(21) 应改为

$$ q_{m}^{T}k_{n}=<f_{q}(x,m),f_{k}(x,n)>=R e[(x_{m},x_{n},m-n)] $$

$q_{m}$ 为例，假设 $\cdot e^{i m\theta}$ 表示为模长为1的复数，根据复数乘法的几何意义， $(W_{q}x_{m})e^{i m\theta}$ 变换实际上对应着向量 $W_{q}x_{m}$ 的旋转，所以我们称之为“旋转式位置编码”，它还可以写成矩阵形式：

$$ q_{m}=\left(\begin{array}{l l}{{c o s m{\theta}}}&{{-:s i n{m\theta}}}\ {{s i n{m\theta}}}&{{c o s m{\theta}}}\end{array}\right)W_{q}x_{m} $$

$q_{m}$ 为例,考虑多维情况，可以得到旋转式位置编码的一般形式为： $q_{m}=R_{\Theta,m}^{d}W_{q}x_{m}$

$$ \begin{array}{r}{R_{\Theta,m}^{d}=\left(\begin{array}{c c c c c c c c}{\cos m\theta_{1}}&{-\sin m\theta_{1}}&{0}&{0}&{\cdots}&{0}&{0}\ {\sin m\theta_{1}}&{\cos m\theta_{1}}&{0}&{0}&{\cdots}&{0}&{0}\ {0}&{0}&{\cos m\theta_{2}}&{-\sin m\theta_{2}}&{\cdots}&{0}&{0}\ {0}&{0}&{\sin m\theta_{2}}&{\cos m\theta_{2}}&{\cdots}&{0}&{0}\ {\vdots}&{\vdots}&{\vdots}&{\vdots}&{\ddots}&{\vdots}&{\vdots}\ {0}&{0}&{0}&{0}&{\cdots}&{\cos m\theta_{d/2}}&{-\sin m\theta_{d/2}}\ {0}&{0}&{0}&{0}&{\cdots}&{\sin m\theta_{d/2}}&{\cos m\theta_{d/2}}\end{array}\right)}\end{array} $$

5.3 旋转位置编码 RoPE 有什么优点？

旋转位置编码通过绝对位置编码的方式实现了相对位置编码，有良好的外推性。

5.4 旋转位置编码 RoPE 被哪些 LLMs 应用？

LLaMA、GLM-130B、PaLM等大语言模型就采用了旋转位置编码ROPE。

六、长度外推问题篇

6.1 什么是 长度外推问题？

• 长度外推问题：训练、推理的长度不一致问题，主要体现在以下两方面：• 问题一：位置编码不一致（推理的时候有训练没见过的位置编码）；• 问题二：attention span大小不一致（推理的时候attention span更大，导致墒增）；

6.2 长度外推问题 的 解决方法 有哪些？

• 问题一解决方法：ALIBI、KERPLE、Sandwich、XPOS、PI、NTK-RoPE(目前看起来这个最强，不用finetune)；
·问题二解决方法：softmax的时候加一个log512n系数;

七、 ALiBi (Attention with Linear Biases)篇 7.1 ALiBi (Attention with Linear Biases) 思路是什么？

在计算完attention score后，直接为attention score矩阵加上一个预设好的偏置矩阵

7.2 ALiBi (Attention with Linear Biases) 的偏置矩阵是什么？有什么作用？

• ALiBi的偏置矩阵：根据q和k的相对距离来惩罚attention score• 作用：相对距离越大，惩罚项越大相当于两个token的距离越远，相互贡献就越小。

7.3 ALiBi (Attention with Linear Biases) 有什么优点？

ALiBi位置编码有良好的外推性

7.4 ALiBi (Attention with Linear Biases) 被哪些 LLMs 应用？

BLOOM就采用了这种位置编码