MOE（Mixture-of-Experts）篇

来自： AiGC面试宝典

• MOE（Mixture-of-Experts）篇

• 一、为什么需要 MOE（Mixture-of-Experts）？
• 二、MOE（Mixture-of-Experts）的思路是什么样的？
• 三、介绍一下 MOE（Mixture-of-Experts）分布式并行策略？• 3.1 MOE $^+$ 数据并行?• 3.2 MOE $^+$ 模型并行?
• 四、MoE大模型具备哪些优势？
• 五、MoE大模型具备哪些缺点？
• 六、MoE为什么可以实现更大模型参数、更低训练成本？
• 七、MoE如何解决训练稳定性问题？
• 八、MoE如何解决Fine-Tuning过程中的过拟合问题？
• 致谢

一、为什么需要 MOE（Mixture-of-Experts）？

• 模型和训练样本的增加，导致了训练成本的平方级增长；• 如何在牺牲极少的计算效率的情况下，把模型规模提升上百倍、千倍？

二、MOE（Mixture-of-Experts）的思路是什么样的？

MOE（Mixture-of-Experts）作为一种基于稀疏 MoE 层的深度学习模型架构，能够将大模型拆分成多个小模型(专家，expert)，然后在每轮迭代过程中，根据样本数量决定激活一定量的专家用于计算，实现节省计算资源的目的；同时，MOE（Mixture-of-Experts）引入可训练并确保稀疏性的门( gate )机制，以保证计算能力的优化。与密集模型不同，MoE 将模型的某一层扩展为多个具有相同结构的专家网络( expert )，并由门( gate )网络决定激活哪些 expert 用于计算，从而实现超大规模稀疏模型的训练。
以下图为例，模型包含 3 个模型层，如(a)到(b)所示，将中间层扩展为具有 n 个 expert 的 MoE 结构，并引入Gating network 和 Top_k 机制，MoE 细节如下图(c)所示。

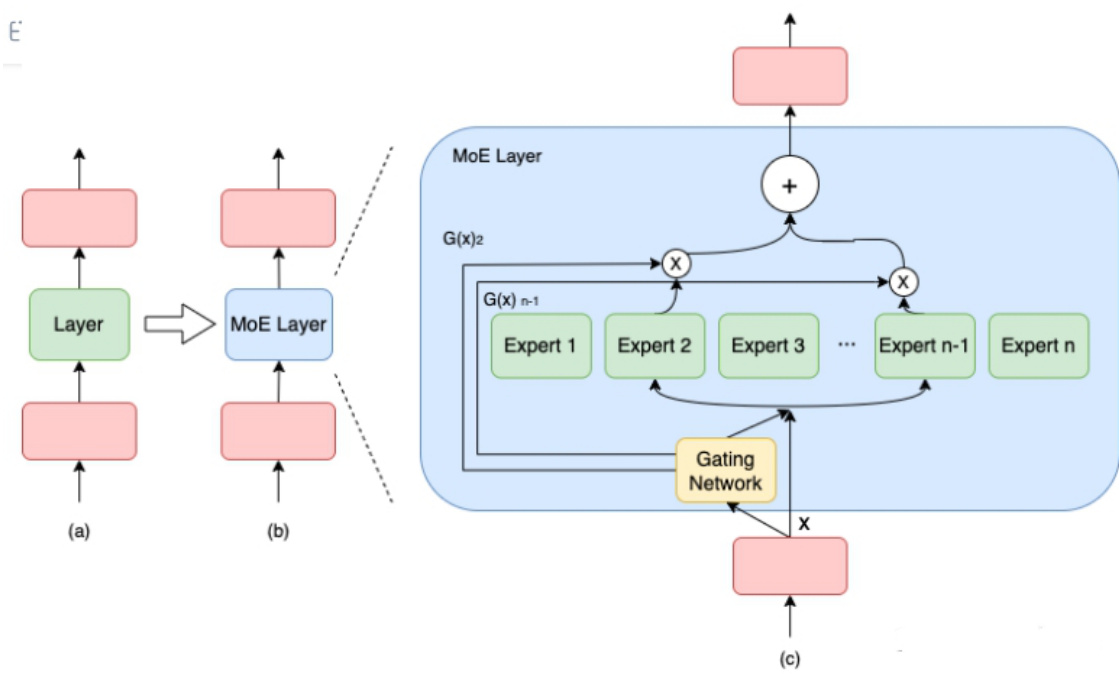
MOE（Mixture-of-Experts）细节

计算过程如下述公式：

$$ \begin{array}{c}{{M o E\left(x\right)=\sum_{i=1}^{n}\left(G\left(x\right){i}E{i}\left(x\right)\right)}}\ {{G\left(x\right)=T o p K\left(s o f t m a x\left(W_{g}\left(x\right)+\epsilon\right)\right)}}\end{array} $$

注：上述第 1 个公式表示了包含 n 个专家的 MoE 层的计算过程。具体来讲，首先对样本 $\mathsf{x}$ 进行门控计算， W 表示权重矩阵；然后，由 Softmax 处理后获得样本 x 被分配到各个 expert 的权重；然后，只取前 k (通常取 1 或者 2）个最大权重；最终，整个 MoE Layer 的计算结果就是选中的 $\mathsf{k}$ 个专家网络输出的加权和。

三、介绍一下 MOE（Mixture-of-Experts）分布式并行策略？

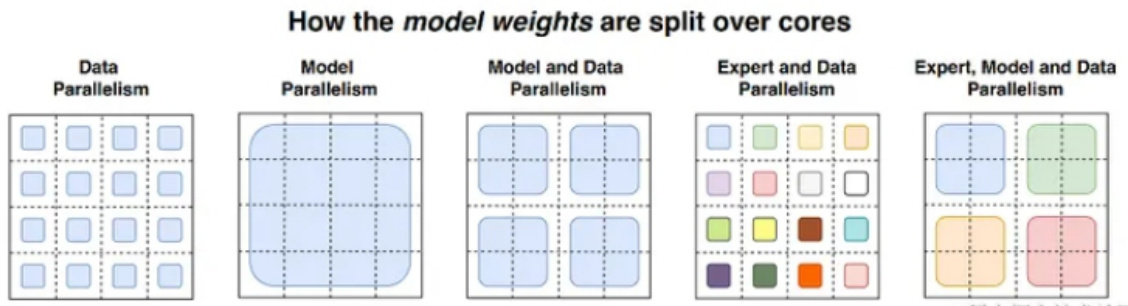
3.1 MOE $^+$ 数据并行?

在数据并行模式下包含MOE架构，门网络(gate)和专家网络都被复制地放置在各个运算单元上。下图展示了一个有三个专家的两路数据并行MoE模型进行前向计算的方式。

该方式通常来说，对于现有的代码侵入性较小。但该方式唯一的问题是，专家的数量受到单个计算单元(如：GPU)的内存大小限制。

3.2 MOE $^+$ 模型并行?

该策略门网络依然是复制地被放置在每个计算单元上，但是专家网络被独立地分别放置在各个计算单元上。因此，需引入额外的通信操作，该策略可以允许更多的专家网络们同时被训练，而其数量限制与计算单元的数量(如：GPU数量)是正相关的。

下图展示了一个有六个专家网络的模型被两路专家并行地训练。注意：专家1-3被放置在第一个计算单元上，而专家4-6被放置在第二个计算单元上。

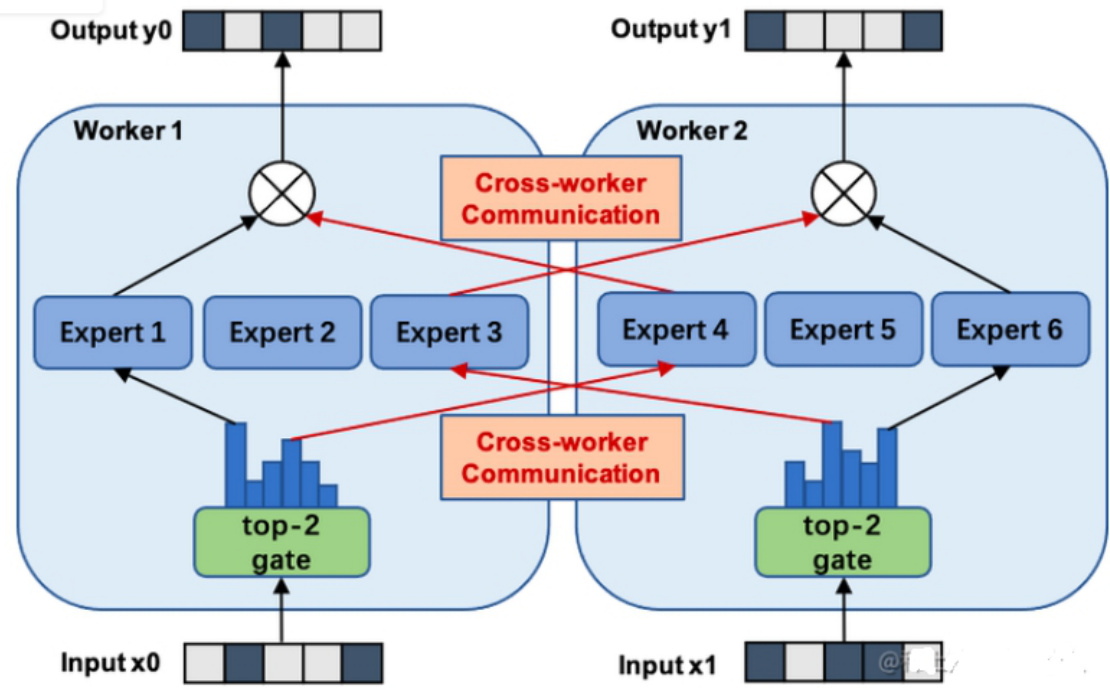
该模式针对不同的模型和设备拓扑需要专门的并行策略，同时会引入额外的通信，因此，相较于数据并行 $^{\cdot+}$ MOE策略，侵入性更强。

除了上述两种MOE并行方案之外，还可以MOE $^+$ 数据并行 $+,$ 模型并行、MOE $^+$ ZeRO增强的数据并行等。

四、MoE大模型具备哪些优势？

训练速度更快，效果更好。
相同参数，推理成本低。
扩展性好，允许模型在保持计算成本不变的情况下增加参数数量，这使得它能够扩展到非常大的模型规模，如万亿参数模型。
多任务学习能力：MoE在多任务学习中具备很好的新能（比如Switch Transformer在所有101种语言上都显示出了性能提升，证明了其在多任务学习中的有效性）。

五、MoE大模型具备哪些缺点？

训练稳定性：MoE在训练过程中可能会遇到稳定性问题。
通信成本：在分布式训练环境中，MoE的专家路由机制可能会增加通信成本，尤其是在模型规模较大时。
模型复杂性：MoE的设计相对复杂，可能需要更多的工程努力来实现和优化。
下游任务性能：MoE由于其稀疏性，使得在Fine-tuning过程中容易出现过拟合。

六、MoE为什么可以实现更大模型参数、更低训练成本？

MoE 使用了混合精度的方法，例如用 bfloat16 精度训练专家，同时对其余计算使用全精度进行。较低的精度可以减少处理器间的通信成本、计算成本以及存储 tensor 的内存。这主要是因为稀疏路由的原因，每个 token 只会选择 top-k 个专家进行计算。同时可以使用模型并行、专家并行和数据并行，优化 MoE 的训练效率。而负载均衡损失可提升每个 device 的利用率。

七、MoE如何解决训练稳定性问题？

可以通过混合精度训练、更小的参数初始化，以及 Router z-loss 提升训练的稳定性。

八、MoE如何解决Fine-Tuning过程中的过拟合问题？

可以通过更大的 dropout （主要针对 expert）、更大的学习率、更小的 batch size。目前看到的主要是预训练的优化，针对 Fine-Tuning 的优化主要是一些常规的手段。

80_MOE_Mixture_of_Experts_篇

文章目录