03|如何设置合适的安全强度?
文章目录
你好,我是范学雷。
上一讲,我们讨论了单向散列函数,以及它是怎么解决数据完整性问题的。你还记得它解决问题的背后逻辑吗?就是因为单向散列函数有两个重要的特点:逆向运算困难和构造碰撞困难。
这两个特点使得我们仅仅修改数据中的一位,所得到的散列值和之前的相比,就会发生很大的变化。所以我们说,这两个困难也决定了一个单向散列函数的破解难度。
逆向运算越困难,破解难度越难;构造碰撞越困难,破解难度也越难。这点你应该懂了,但是,你有没有想过,困难程度要多大,才算困难?有什么指标可以衡量单向散列函数的破解难度?
一下出现这么多问题,是不是有点意外?其实,密码学就是在和千奇百怪的问题 的 纠缠中获得进展的。这一次,我们来讨论困难有多难以及和破解难度相关的问题。
困难要有多难?
我们要探讨的第一个问题就是,一个单向散列函数的逆向运算和构造碰撞要困难到什么程度,它才能算是一个合格的单向散列函数呢?如果凭感觉,在密码学的实践 中 , 我们心中“完美”的 单向散列函数,应该困难到没有人可以逆向运算,也没有人可以构造碰撞。
可是,只要有人发现了有那么一对数据具有相同的散列值,不管这个人什么出身、什么来历,也不管这对数据有多么的千奇百怪,更不管破解方式是多么的不合常理,这个结果就意味着这个单向散列函数被破解了,不再安全了。
比如说,下面的两段数据具有相同的 MD5 算法散列值(MD5 是一个单向散列函数)。
细心看的话,你会注意到例子中的 afbfa202 和 afbfa200,以及 6da0d1d5 和 6da0d155 这两段数据是有差异的,但是结果显示,它们的散列值却是相同的。在这个例子里,我们并不需要深入了解破解 MD5 的具体算法和实现,我们只需要知道 MD5 被破解了,MD5 就不能够继续使用了。
M1:
4dc968ff 0ee35c20 9572d477 7b721587 d36fa7b2 1bdc56b7 4a3dc078 3e7b9518 afbfa202 a8284bf3 6e8e4b55 b35f4275 93d84967 6da0d1d5 5d8360fb 5f07fea2
M2:
4dc968ff 0ee35c20 9572d477 7b721587 d36fa7b2 1bdc56b7 4a3dc078 3e7b9518 afbfa200 a8284bf3 6e8e4b55 b35f4275 93d84967 6da0d155 5d8360fb 5f07fea2
Hash: MD5(M1) = MD5(M2)
008ee33a 9d58b51c feb425b0 959121c
我所了解的现代单向散列函数 在 算法意义上的破解,都是通过宣布找到一对散列值碰撞的数据的形式发布的。还记得什么是散列值碰撞吧?就是指两份散列值的数据是相同的。
只有当你找到了这样的一对碰撞,你才能验证破解算法的有效性,算法的破解才能让人信服。
不过,话说回来,这固然是一个好的办法,可是对于还没有被破解的算法,有没有更直观的指标让我们感受它有多安全呢?对于已经破解的算法,有没有直观的指标让我们感受它有多脆弱呢?
在密码学这么讲究量化的领域,当然不会缺少了这样的指标。其中,最常用的指标就是安全强度(Security Strength)。
什么是安全强度?
在密码学中,安全强度通常使用“位”(字节位)来表述。比如说,安全强度是 32 位。这里的“位”是什么意思?N 位的安全强度表示破解一个算法需要 2^N(2 的 N 次方) 次的运算。
为什么要使用“位”来表示安全强度?因为这样的话,我们就可以很方便地比较不同算法的安全级别,在同一个安全级别上组合不同的安全算法。比如说,MD5 的安全强度是不大于 18 位,1024 位的 RSA 密钥的安全强度是 80 位,SHA-256 算法的安全强度是 128 位。
在这里给你出个小问题,如果我们把上面这几个算法安排成一个组合,这个组合的强度是怎样的?这个组合的强度并不高,因为组合的强度,由最弱的算法和密钥决定。所以,把它们安排成一个组合,不是一个好的想法。你可以先记下来,我们后面会再讨论算法组合的基本原则。
回到安全强度这个话题,谈论单向散列函数算法之前,让我们先来感受一下安全强度。比如 MD5,我们说了,它的安全强度最多 18 位,也就是说,我们运算 2^18=262144 次就可以破解,按现在的计算机一毫秒一次运算的速度计算,需要 262144 毫秒,折合 4.34 分钟。
嗯,MD5 现在就是这么弱。其实,在 2006 年,就有研究者宣布研究成功,即使是那时候的笔记本电脑,在一分钟之内也可以找到一对散列值碰撞的数据了。
那 128 位的安全强度呢?假设我们现在有一台速度快 1000 倍的计算机,它能做到 1 纳秒运算一次。如果我们做类似上面的运算,即使我们同时使用 10 亿台计算机,破解它也需要一千万个十亿年。80 位的安全强度,同样的条件,破解大概需要 38 年。
从上面的计算,相信你可以感受到,只是稍微增加几十位的安全强度,破解难度就有巨大的提升。因为,破解难度是安全强度位数的指数(2^N)。所以,在 实践 中,我们应该优先选择安全强度足够高的算法。
安全强度会变吗?
每一个密码算法诞生的时候,都有一个理论上的设计安全强度。注意,理论上的意思就是有可能与实际情况不符。比如单向散列函数 SHA-1 在 1993 年发布的时候,它的设计安全强度是 80 位。
12 年后,在 2005 年 2 月,中国密码学家王小云教授带领的研究团队发现,SHA-1 的安全强度小于 69 位,远远小于设计的 80 位。从此,SHA-1 的安全强度开始一路衰减。很快,2005 年 8 月,王小云教授的团队又改进了破解算法,发现 SHA-1 的安全强度只有 63 位了。
2015 年 10 月,密码学家马克·史蒂文斯(Marc Stevens),皮埃尔·卡普曼(Pierre Karpman)和托马斯·佩林(Thomas Peyrin)的研究团队发现 SHA-1 的安全强度只有 57.5 位。
更要紧的是,他们估算,如果使用云计算,按照 2015 年亚马逊 EC2 云计算的定价和算力,57 位的安全强度,2015 年的破解成本大致是 10 万美元,你可以感受下密码强度和破解成本的数字。
2020 年 1 月,密码学家盖坦·勒伦(GaëtanLeurent)和托马斯·佩林(Thomas Peyrin)又发现,SHA-1 的攻击复杂度是 63.4 位,攻击成本大约为 4.5 万美元。
根据上面的数字,我们可以感受到,一个 64 位安全强度的密码算法,它现在的破解成本大概是 5 万美元左右。不同类型的算法,破解成本也许有很大偏差,但是我们依然可以大致估算攻击成本。5 万美元,无论是对于一个有组织的研究机构,还是犯罪集团,都是一个很小的数目。
这可以说明什么?如果一个系统的安全强度低于 64 位,它的安全性几乎形同虚设。
通过 SHA-1 的例子,我想强调的就是,一个算法的安全强度不是一成不变的。随着安全分析的进 步 ,几乎所有密码学算法的安全强度都会衰减。今天看起来安全的算法,明天也许就有破解的办法。所以,一个好的安全协议,应该考虑备份计划和应急计划(参见极客时间《代码精进之路》专栏第 41 讲,“预案,代码的主动风险管理“里提到的双引擎和降落伞设计)。
使用多大的安全强度?
现在,我们已经知道了什么是安全强度,也感受了一下不同密码算法的安全强度,知道了安全强度是会变的。那么,我们今天要讨论的最后一个话题是,我们该使用多少位的安全强度?
多少位的安全强度算是安全的呢?其实,我们要是想找到一个确切的答案,我们不仅要看具体的使用场景,还要综合考虑性能和安全强度。是不是觉得会有点复杂和困难?
不过,我 可以给你一个 建议,就是 参考、遵 循常用的推荐指标。
业界内最新推荐的三个常用指标分别是:
- 美国的 NIST(国家标准技术研究所);
- 德国的 BSI(联邦信息安全办公室);
- 欧洲的 ECRYPT-CSA(欧洲卓越密码网络)。
为了让你更直观地了解这三个指标,我还给你做了一个小结。
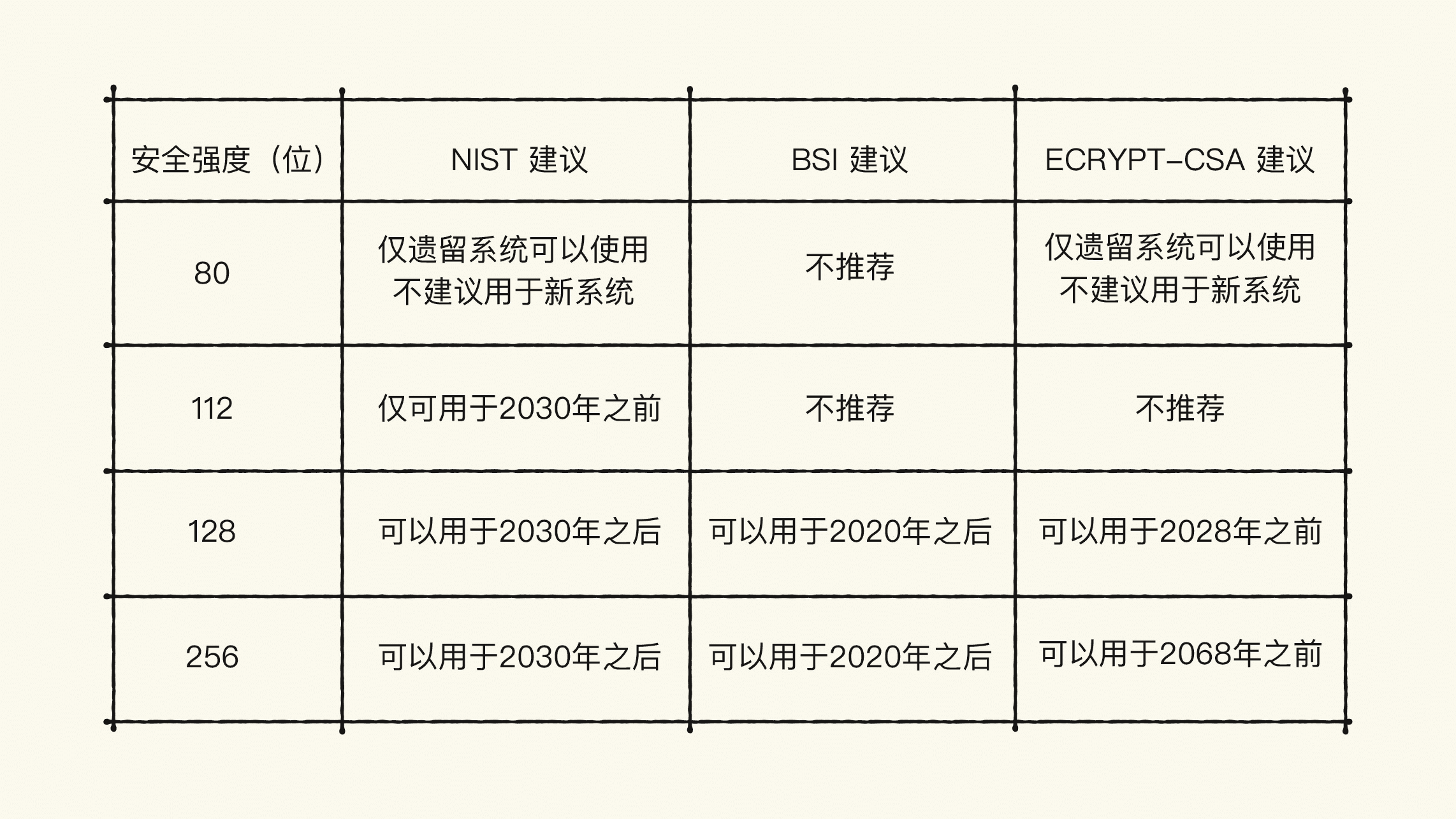
看到这个表,是不是感觉还是摸不到头脑?该怎么使用这个表呢?我们一起来看一个例子。
假设,我们现在要设计一个新系统,预期寿命十年,也就是,我们要从 2020 年开始运营,运营到 2030 年结束。而且我们还要保证到 2030 年,这个系统还是足够安全的。
首先,我们按照 NIST 的建议,2030 年后,112 位的安全强度已经不能使用了,所以,如果我们遵守 NIST 的推荐指标,这个系统就不建议选择 112 位安全强度的算法。
在 BSI 建议里,2030 年之前够用的话,我们应该选择 256 位的安全强度。
我们再看 ECRYPT-CSA 的建议,128 位的安全强度只能用于 2028 年之前。到了 2030 年,128 位的安全强度就不能满足 ECRYPT-CSA 的建议了。所以,如果我们遵循 ECRYPT-CSA 的建议,这个系统就需要使用 256 位的安全强度。
你发现了吗,ECRYPT-CSA 的建议为什么这么保守?其实,这种保守的姿态背后,隐含了对量子计算时代来临的担忧。在量子计算时代,128 位的安全强度稍显脆弱,可是 256 位的安全强度还是足够的。虽然量子时代还没有到来,但是我们现在就要开始考虑量子时代的挑战了。
从上面的推荐,我们可以看到,128 位的安全强度,目前来说是安全的。不过,一个需要长期运营的系统,如果性能瓶颈不是问题,现在就可以 开始 考虑使用 256 位强度的密码算法了。
还记得我们上面提到的安全强度不足 18 位的 MD5 函数吗?这么弱的安全强度,几乎已经没有实用价值了。那么,有哪些单向散列函数能达到 128 位,甚至 256 位的安全强度?这些问题,我们下一次来讨论。
Take Away(今日收获)
今天,通过讨论单向散列函数的“两个困难程度”,我们知道了困难有多难,还分析了破解强度的计量办法、安全强度的衰减、常见的安全强度推荐指标,以及一些可以直观感受的数字。
这些直观感受的数字可以帮助你建立对密码算法安全强度的印象。比如,一个 64 位安全强度的密码算法,它现在的破解成本大概是 5 万美元左右。再比如,128 位的安全强度,按照现有的计算能力,破解它需要一千万个十亿年。
这一讲,通过对安全强度的讨论,我们要:
- 知道 密码学 安全强度通常使用位来表示;
- 知道 128 位的安全强度 暂时 还是安全的;
- 知道长期的系统可以考虑开始使用 256 位安全强度的算法了。
思考题
如果你能够使用你知道的所有的计算机,包括你的个人计算机和公司的计算机系统(比如亚马逊的云系统),你能不能大概估算一下,破解 64 位的安全强度、80 位的安全强度、128 位的安全强度,分别都需要多长时间?
这是一个能够帮助你建立对安全强度直观概念认知的办法。
欢迎在留言区留言,记录、讨论你的估算数据。
好的,今天就这样,我们下次再聊。
文章作者 anonymous
上次更新 2024-01-30