08|该怎么选择初始化向量?
文章目录
你好,我是范学雷。
上一讲,我们讨论了对称密钥的常见算法,还讲到了序列算法和分组算法。还记得吗?当时,我建议你优先使用序列算法,因为它有着良好的性能和皮实的用法。另外,我还向你推荐了 AES-256 和 AES-128。
但是,由于我们还没有考虑数据分组等因素的影响,所以这个建议的实用性还有待商榷。那么,这一讲,我们就来看看对于分组算法,到底有哪些麻烦?我们又该怎么避免这些麻烦?
其实,这是一个解决起来很复杂的问题。不过,今天我们可以先对问题建立一个初步的认知。
要知道分组算法有哪些麻烦,就要先知道该怎么计算分组算法。
分组算法怎么计算?
我们在上一讲说过,分组算法要对输入数据进行分组,然后按数据分组来进行运算。一个典型的分组算法,一般要由三个部分组成,数据分组、分组运算和链接模式。

我们先来看看数据分组是怎么一回事。
数据分组在加密时,会把明文的输入数据分割成加密函数能够处理的数据块。比如,AES 算法能够处理的数据块大小是 128 位,那么,输入数据就要被分割成一个或者多个 128 位的小数据块。
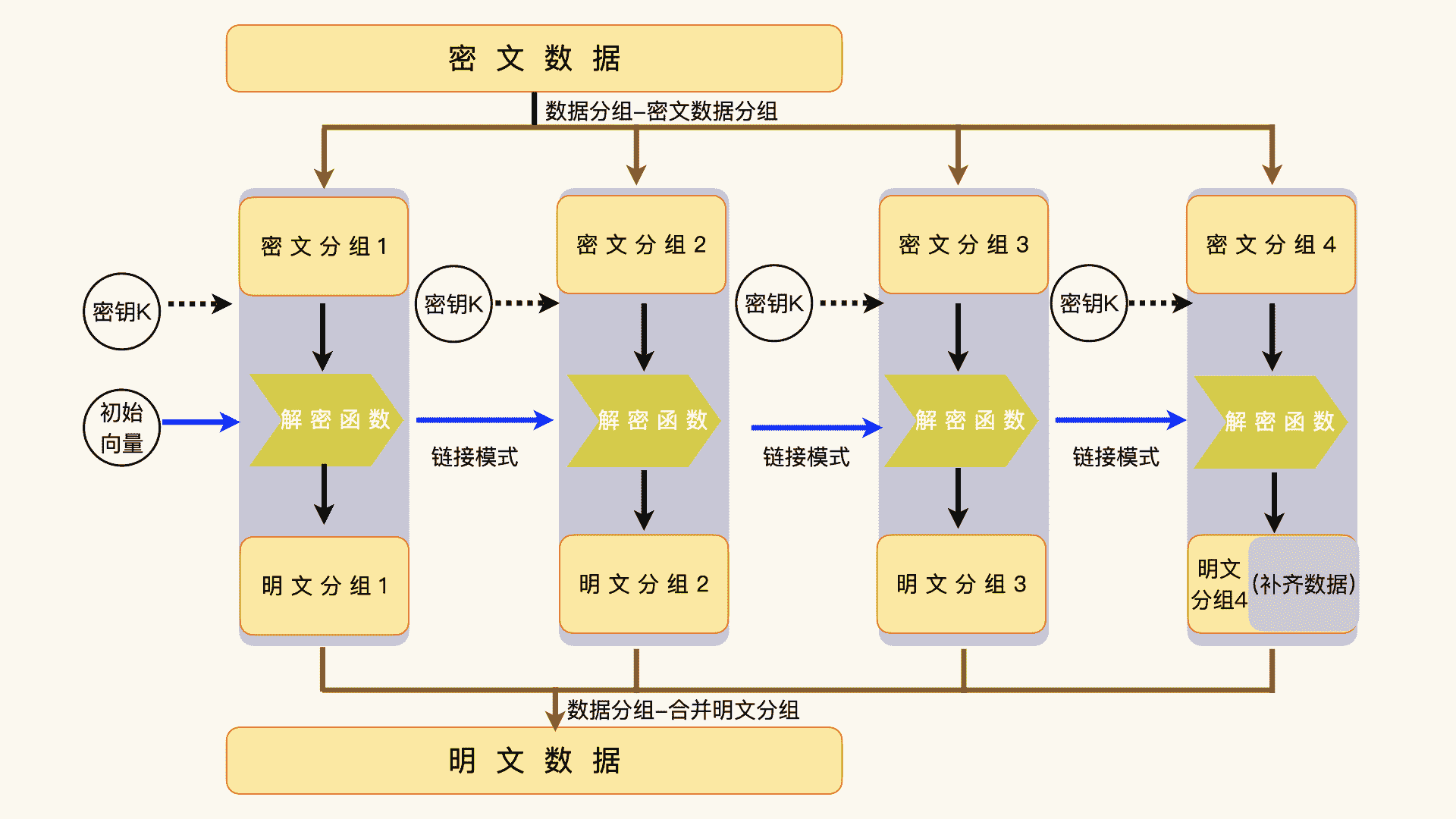
如果不能整分,就要把最后一个分组补齐成 128 位。这些分组数据的运算结果,组合起来就是密文数据。解密时,执行相反的操作,把补齐数据去掉,再把数据分组组合成完整的明文数据。
理解了数据分组,我们再来看分组运算和链接模式。
分组运算,意思就是把每一个明文数据分组通过加密函数,转换成密文数据分组。而链接模式,指的是如何把上一个分组运算和下一个分组运算联系起来。
有一点需要说,第一个分组运算并没有上一个分组运算可以使用,这时候,我们就需要引入一个初始化的数据,来承担“上一个分组运算”向下链接的功能。这个初始化的数据,我们一般称为初始化向量。
那你有没有想过,我们为什么要把上一个分组运算和下一个分组运算联系起来呢?其实,我们在前面讨论过单向散列函数的链接模式,我们说它是为了确保雪崩效应能够延续。
在分组运算里,链接模式也承担类似的功能:
- 不同的明文数据,它的密文数据应该是完全不同的,即使明文数据里包含相同的数据分组;
- 相同的明文数据,每一次的加密运算,它的密文数据也应该是完全不同的。
什么影响算法的安全性?
现在,我们已经梳理了一遍分组算法的运算过程了。这样,我们就能够在其中找到影响分组算法的关键因素。这些因素,也就是影响分组算法安全性的因素。
在数据分组里,把输入数据分割成固定大小的数据块这一部分,除了数据补齐之外,没有什么变数。所以,我们可以发现,数据补齐方案才是影响分组算法的关键部分。
这样,我们就不难找出下面的五个因素:
- 加密函数和解密函数;
- 密钥;
- 初始化向量;
- 链接模式;
- 数据补齐方案。
通过上一讲的讨论,我想我们都了解加密函数、解密函数和密钥在分组算法中的重要地位了。如果加密函数不安全,整个分组算法的安全性也就坍塌了;如果密钥没有做好保密或者密钥质量不好,数据的保密性也就无从谈起。
比如说,我们经常看到宣传,说什么采用了 AES-256 算法,安全强度有保障;说什么只有造一台时光机,穿越回历史现场,才能破解一个应用。这些说法,有它的道理,但是仅仅依据这些信息,还不能确认一个算法的使用和运算是不是安全的。
另外三个因素,就是经常被我们忽视的因素。那么,它们是怎么影响算法安全性的呢?
初始化向量怎么选?
我们今天先讨论第一个影响的因素:初始化向量。
我们要想了解初始化向量对算法安全性的影响,就要先看看第一个数据块是怎么计算的,第一个数据块和初始化向量关系紧密。第一个数据块的计算,它的输入信息包括:
- 密钥;
- 初始化向量;
- 第一个明文数据分组。
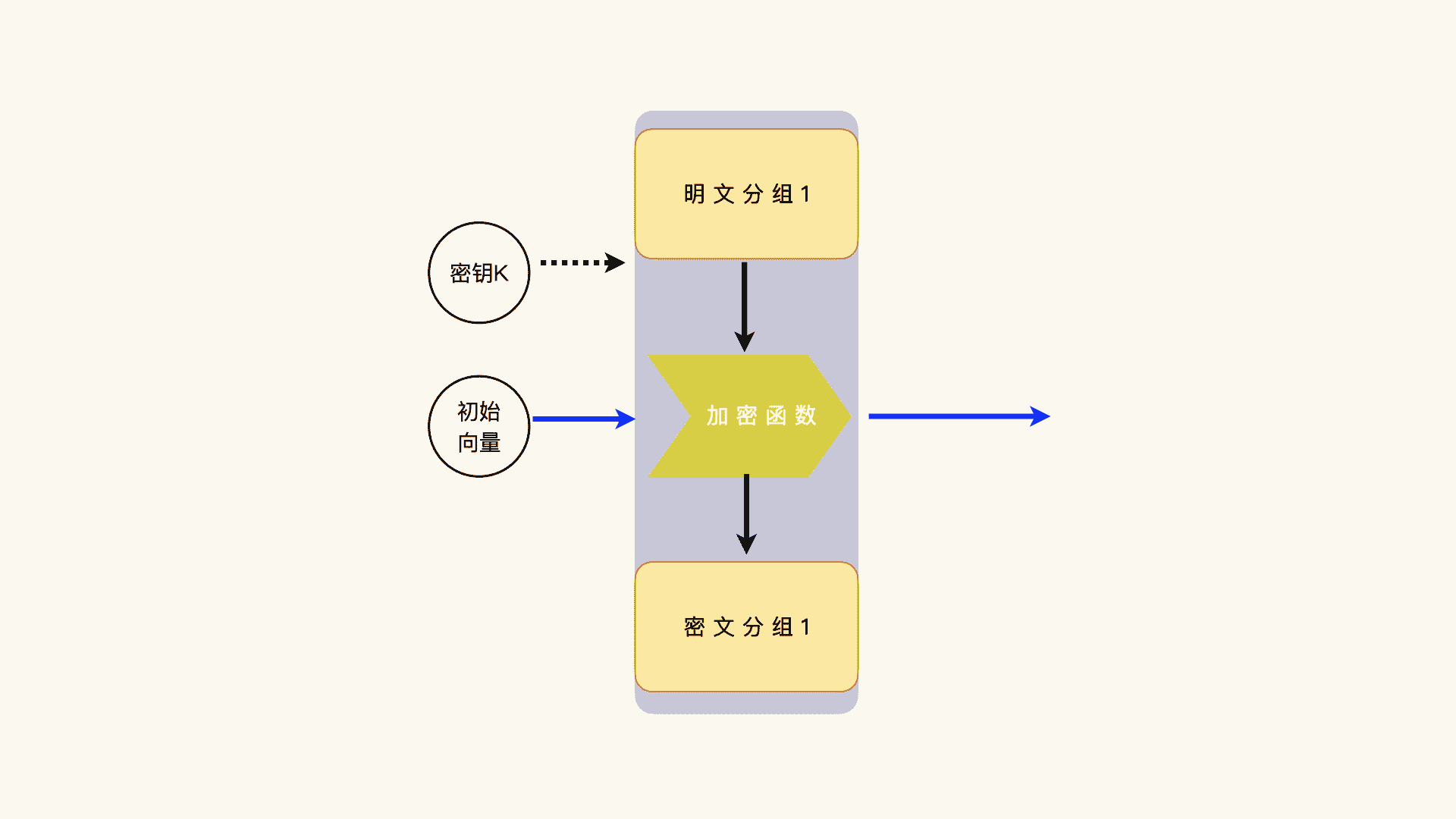
如果我们能够确定这些输入信息,那么输出的第一个密文数据分组也就确定了。
一般来说,一个对称密钥要使用多次,对多个明文数据进行加密运算。如果存在第一个明文数据分组相同的两段数据,并且使用了相同的初始化向量,那么第一个密文数据分组就是相同的。
也就是说,相同的输入,就会有相同的输出。
对于大部分算法而言,分组数据块都比较小,比如,AES 算法的分组数据块大小是 16 个字节。这样,在实际应用中,就比较容易构造相同的数据块,或者存在相同的数据块。
在现实的应用里,也存在大量的、重复的、已知的数据,比如 HTTP 协议的头部数据。如果我们需要保密的数据恰好重复了一段已知的明文,攻击者就可以根据密文数据是不是相同,来猜测、寻找明文数据。这样的话,就破坏了数据的保密性。
但是,我们在使用加密运算时,大部分时候都没有办法确定明文数据会不会有重复数据,以及重复数据会不会是一次加密运算的第一个数据块。所以,如果不想暴露重复数据的机密性,我们只能在初始化向量这一个因素上想办法。因为,密钥是相同的,如果第一个明文数据分组也是相同的,只剩下初始化向量这一个输入信息可以控制了。
在一个对称密钥的生命周期里,初始化向量不能重复,这是使用对称密钥算法的第一个要求。
这个要求看似简单,其实做起来并不容易。一个单纯的加密算法的实现,一般没有办法记住一个初始化向量有没有用过。这就需要应用程序的开发者自己想办法,常见的办法有两种:
- 使用安全强度足够的随机数作为初始化向量;
- 使用序列数,下一次的初始化向量的数值,比上一次的数字自动加一或者自动减一。
不过,这两种初始化向量的选择,还是各有各的问题,我们需要注意。
第一种,随机数的获取,有时候不是一个有效率的运算。如果随机数发生器选择不当,还会造成加密运算的阻塞,进一步降低加密运算的效率。另外,由于解密需要相同的初始向量,如何在加密端和解密端同步初始化向量,也是一个需要考虑的问题。
一个常见的解决办法,就是把初始化向量和加密数据一起发送给对方。
第二种的话,使用序列数,需要保持序列数的状态,还需要加密运算的同步。不过,序列数状态的保持和同步,除了效率之外,还会衍生出其他的待解决的问题,比如分布式计算环境下的序列数同步问题,比如攻击者会知道每一个初始化向量的问题。
如果你能够看到的问题无法解决,可以考虑使用随机数作为初始化向量。
你看,初始化向量选择充满了复杂性,一般的密钥算法库都不会提供缺省的、自动的初始化向量。应用程序需要根据使用场景来制定适当的初始化向量选择方案,这是一个容易忽略的要求。
一个密钥能用多少次?
在这一讲的最后,我们来讨论一个话题,一个密钥有没有使用次数的限制呢?为什么要在这一讲讨论这个话题呢?因为,我想,这是一个恰当的时机。
前面,我们讨论了,在一个对称密钥的生命周期里,初始化向量不能重复。也就是说,对于一个算法来说,初始化向量的长度是固定的。长度固定,也就意味着初始化向量的个数是有限制的。
比如,一个 128 位的初始化向量,最多有 2^ 128 个不重复的数值。进一步的说,对于这个算法,一个密钥最多只能使用 2^ 128 次。的确看起来,2^128 是一个巨大的数字,一般的应用程序也没有什么机会使用这么多次加密运算。
当然,还有其他因素限制密钥的使用次数。很多限制因素的叠加,就会使得密钥使用的限制数远远低于初始化向量的许可数目。所以,我们心里一定要知道,密钥是有使用次数限制的,并且要有检查密钥使用次数限制的习惯。
这是一个不太引人注意的安全陷阱,也是近几年才受到广泛关注的算法安全问题。我们后面还会讨论其他的限制条件,并且我会罗列出来不同算法的使用限制。
之后的两讲,我们就接着今天的话题,看看除了初始化向量之外,链接模式和数据补齐方案是怎么影响对称密钥算法的安全性的?这两个问题的讨论,需要较大篇幅,不过我会带你一起分析。
Take Away(今日收获)
今天,通过解构分组算法的运算,我们讨论了影响分组算法安全性的五个关键因素。然后讨论了选择初始化向量应该注意的陷阱,也就是说,在使用对称密钥加密时,初始化向量不能重复。
最后,我们还讨论了一个不太容易受关注的问题,就是密钥是有使用次数限制的。一般的应用程序,密钥使用次数限制不是问题,但是如果你要设计一个广泛使用的协议,还是要考虑密钥这个限制的。密钥使用次数用完之前,一定要更新密钥。
今天,我们应该理解、记住:
- 分组算法的处理过程;
- 影响对称密钥算法安全性的五个关键因素;
- 在一个对称密钥的生命周期里,初始化向量不能重复。
思考题
今天的思考题,也是一个动手题。
在你正在开发的项目中,或者你关注的开放源代码项目中,试着搜索一下初始化向量的使用。看一看对于同一个对称密钥,初始化向量会不会重复,有没有可能重复。如果一个对称密钥使用了重复的初始化向量,有没有潜在的安全风险?你有没有什么建议?
欢迎在留言区留言,记录、讨论你的发现和建议。
好的,今天就这样,我们下次再聊。
文章作者 anonymous
上次更新 2024-01-30