10|怎么防止数据重放攻击?
文章目录
你好,我是范学雷。
上一讲,我们讨论了对称密钥分组算法的链接模式,从链接模式出发,我们还分析了 ECB 模式,初始化向量和链接模式的缺失导致了 ECB 模式的安全缺陷,尤其是数据重放攻击。
我们说,有密码学基础知识的工程师,都应该知道 ECB 模式的安全问题,并且不会在应用程序中使用它。这一讲,我们来讨论一个更广泛使用的加密模式,CBC 模式。
CBC 模式,可能是 2018 年之前最常用、最常见的加密模式。和 ECB 模式不同,由于初始化向量和链接模式的使用,CBC 模式解决了数据重放攻击的问题。可是,从 2018 年开始,由于它的安全问题,CBC 模式开始退出历史舞台,尽管这一进程可能需要十数年,甚至数十年。
为什么还要学习 CBC 模式?
不知道你是不是已经有了一个问题:既然 CBC 要退出历史舞台了,我们还学习它干什么呢?
第一个原因,CBC 的退出进程可能需要十数年才能完成。你现在工作的项目种,可能还存在 CBC 模式的大量使用。我们学习了 CBC 模式,有助于你解决现存项目的安全问题。
第二个原因,学习针对 CBC 的攻击方案,是我们深入理解加密算法安全问题的最好的切入点。了解这些安全缺陷和攻击方案,有助于你更好地使用密码学的算法。因为,这些缺陷也可能换个面孔,出现在应用程序层面。如果你能够说清楚 CBC 模式的攻击办法,也就意味着你已经试着走入了算法的细节。
第三个原因,也是最重要的原因,就是我们要进一步地理解初始化向量和链接模式对加密算法的影响。学习 CBC 模式会为我们将来讨论更高级的协议和更安全的算法打下基础。
那么,CBC 模式是什么样子的?它是怎么解决数据重放攻击的?它存在哪些安全陷阱?这是我们这一次要解决的问题。
CBC 模式什么样?
和其他模式不同的是,在 CBC(Cipher Block Chaining)模式中,明文分组在加密之前,要与前一组的密文分组进行异或运算,异或运算的结果会参与加密函数的运算。
也就是说,上一次的密文分组要参与下一次的加密运算,每一个密文数据不仅依赖于它对应的明文分组,还依赖于上一次的密文分组。
这样的话,每一个密文分组,都依赖于前面所有的明文分组,包括初始化向量。
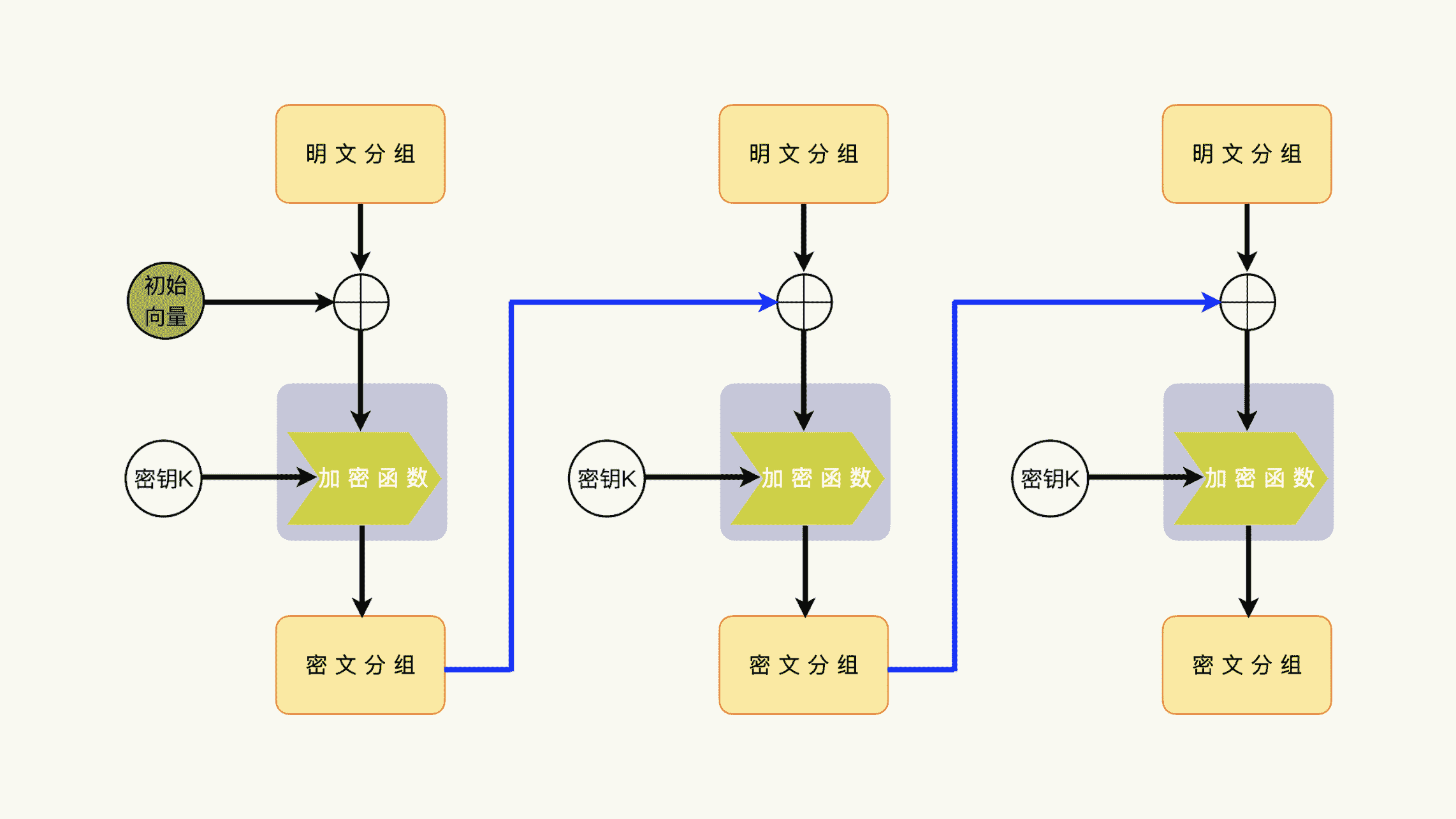
所以,我们能够知道,CBC 模式是需要初始化向量的。最显而易见的原因,就是第一个明文分组还不存在所谓的“上一个密文分组”。所以,我们需要一个外部引入的初始化向量来替代“上一个密文分组”参与运算。
不过,我们需要注意的是,在加密过程中,加密函数的输入数据是明文分组(Mi)和上一次的密文分组(Ci-1)的异或运算的结果(Mi ^ Ci-1)。
在解密过程中,解密函数的输出数据,也是明文分组和上一次的密文分组的异或运算结果(Mi ^ Ci-1)。我们要是想得到解密的明文分组,就需要把明文分组和上一次的密文分组分离开来。
我们现在可以确定的是,上一次的密文分组(Ci-1)是已知的。所以,只要我们把上一次的密文分组和解密函数的输出数据进行异或运算,就把明文分组分离出来了。
(Ci-1) ^ (Mi ^ Ci-1) = Mi
所以,我们可以发现,对于解密过程来说,如果我们把解密函数的运算结果与上一次的密文分组进行异或运算,就可以获得对应的明文分组。
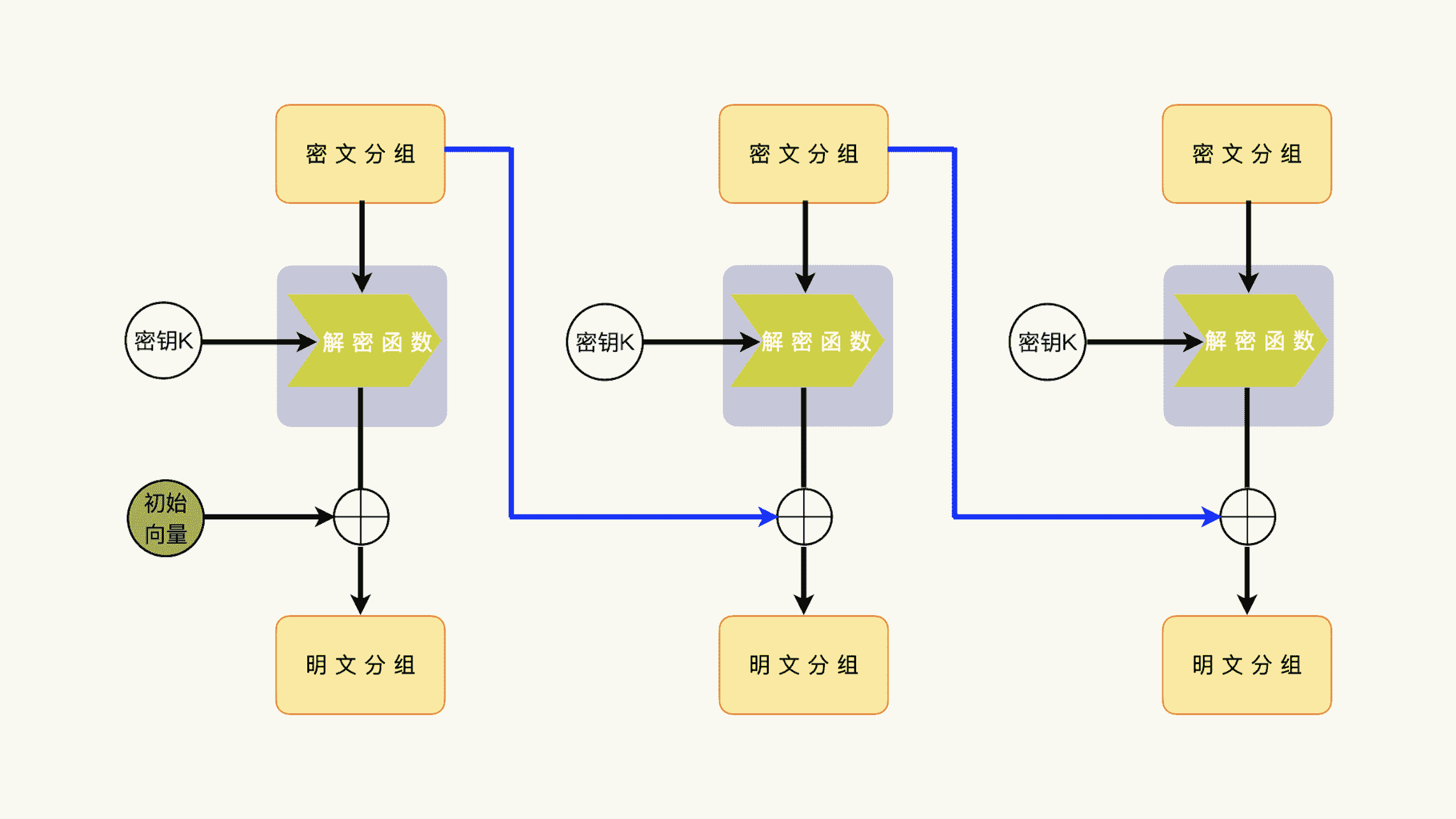
不难想象,在解密过程中,我们要想获得第一个明文分组,用来替代“上一个密文分组”的初始化向量就必须要参与解密的过程。也就是说,加密过程的初始化向量和解密过程的初始化向量必须是一样的,否则,我们就没有办法得到第一个明文分组。
注意一点,初始化向量只影响第一个明文分组,并不影响后续的解密过程和明文分组。
类似地,一个密文分组,只影响它的下一个明文分组,并不影响更后面的解密过程和明文分组。
而在加密过程中,每一个密文分组,都依赖于前面所有的明文分组,包括初始化向量。
所以,我们在这里要注意的就是加密过程和解密过程的区别。这是一个重要的特征,我们先在这里打个伏笔,后面我们会再讨论这个特征有什么用。
总的来说,理解 CBC 模式,我们要把握以下三个关键点:
- 加密和解密要使用初始化向量;
- 加密和解密的初始化向量是等同的;
- 上一次的密文分组参与下一次的加密和解密运算。
初始化向量需要保密吗?
我们讨论过初始化向量的选择问题,就是在一个对称密钥的生命周期里,初始化向量不能重复。
如果每一次运算,初始化向量都 能 不重复,即使是相同的明文数据,它的加密结果也是不同的。但是,如果初始化向量重复使用,相同的明文就会有相同的密文。重复使用的初始化向量, 会 消解密文反馈的作用,使得 CBC 模式和 ECB 模式一样脆弱。
所以,初始化向量的唯一性在加密运算的安全性中至关重要。
那你会问了,既然初始化向量这么重要,那我们需要对它进行保密吗?初始化向量并不需要保密。如果你对这一点有疑问,不妨换个角度想一想:每一个分组加密的初始化向量都是上一次加密运算得到的密文分组,而密文分组是可以公开的信息。
初始化向量不需要保密,这是我们要打的第二个伏笔。
异或运算会不会有问题?
我在上面的讲解中提到了异或运算,其实,它在密码算法里有广泛的应用,为什么它如此广泛?
第一个原因是异或运算是按位运算,所以在相同的计算环境下,异或运算时间只和数据的位数相关,和数据的实际数值无关。放在密码学算法的世界里,如果运算时间和实际数值无关,那简直再好不过了。
换句话说,如果运算时间和数据数值相关,而且别人还了解到这种相关性,他就可以通过统计学的方法,通过观察、测算运算时间,找到运算时间和数据数值之间的关联,来破解密码。
第二个原因同样是按位运算,在相同的计算环境下,异或运算的复杂度,也就是需要的算力,只和数据的位数相关,和数据的实际数值无关。而且,一个运算需要的算力,在计算机环境中,可以通过占用的 CPU 周期数,以及消耗的内存空间来衡量。
同理,如果占用的 CPU 或者消耗的内存和数据数值相关,别人就可以通过统计学的办法,然后观察 CPU 的占用、电力消耗或者内存的消耗,来破解密码。一般来说,这种相关性,也会影响运算时间,从而使得基于测算运算时间的攻击方式同样有效。
不光如此,如果运算的复杂度和数据数值相关,密码破解的办法可就是千奇百怪的了。记录、测算计算机的噪音、温度、辐射、反应时间等等,都有可能成为有效的攻击手段。
如果让一个一流的黑客,拿着手机进入数据中心,录一段服务器发出的声音,说不定你的服务器就被攻陷了。之所以没有说一定会被攻破,是因为近几年的密码学进展,已经发展出了具有防范能力的算法和实现。
但是,如果你的服务器使用的是十年前的技术和软件,黑客得手的概率还是有的。我们后面会讨论这些新技术和新算法。
第三个原因和异或运算的运算特点有关,也就是相同的数据归零,不同的数据归一。
- 归零律:如果两段数据完全相同,它们的异或运算结果,就是每一位都是零的数据;
- 恒等律:如果一段数据和一段全是零的数据进行异或运算,前一段数据中是零的位运算后还是零,是一的位运算后还是一。也就是说,和零进行异或运算,不改变原数据的数值。
正是异或运算的归零律和恒等律,CBC 模式才能成立,解密才能进行。这两个性质,还使得解密运算和加密运算具有相同的运算效率。
然而,CBC 模式的主要安全问题,也来源于异或运算的这两个性质。
如果两段数据中只有一位不同,它们的异或运算结果,就是只有这一位的数据是一,其他的数据都是零。那是不是我们就可以通过构造明文分组或者密文分组,一次改变一位数据,然后把数据交给加密运算或者解密运算来处理,通过观察加密或者解密的结果展开攻击了?
比如说,一个 128 位的密钥,它的强度能承受 2^128 次的运算,是一个强度的指数级别的量级。
- 如果我们一次改变一位数据的攻击方式得逞,最多需要 128 次的运算;
- 如果我们一次只能观测一个字节,一次一位的改变需要 2^8 = 256 次,这样的攻击方式得逞,最多需要 255 * 16 = 4080 次的运算。
这样的运算强度,和设计的理论值 2^128 相差太远了,一次有效的破解也就是分分钟的事情。
还别说,这样的攻击方式在实践中真的是可行的。这种攻击方式,把 CBC 模式变成了一个充满陷阱的模式。用的好,它就是安全的;用的不好,它就会惹来麻烦。这实在不符合密码算法要皮实、耐用的要求。
阻断一个攻击的方式之一,就是破坏攻击依赖的路径或者条件。对于上面的攻击方式,其实只要攻击者没有办法一次改变一位数据或者少量的数据,这样的攻击就可以被有效破解了。
也就是要保证攻击者在展开攻击的时候,没有办法一次改变不少于一个数据分组的数据。对于 AES 来说,数据分组大小是 128 位,攻击者需要运算 2^128 次,才可以攻击得逞。
计算量这么大,攻击者的攻击方式就无效了。那我们怎么做才能让攻击者没办法呢?
密文分组、密钥、加密算法、解密算法,这些都是固定的数据或算法,没有考量的空间。剩下的变量,就只有明文分组和初始化向量了。要想解决掉这个安全问题,该怎么控制明文分组和初始化向量?异或运算又是怎样带来麻烦的?
要想深入地了解这些问题,有点烧脑。下一次,我们集中精力来讨论、分析其中的细节和办法。
密钥少一位会有影响吗?
不知道你有没有注意到,我们上面的讨论,提到了数据的位数。
因为分组加密是按照固定的分组进行加解密运算,所以每一次的分组运算,数据的位数都是固定的。比如,AES 算法的分组大小都是 128 位。所以,我们不用担心分组运算的数据位数的变化。
在分组运算中,初始化向量、密文分组和明文分组密钥的数据位数也都是固定的。所以,我们也不需要担心它们的位数的变化。加密算法和解密算法不涉及数据位数,所以我们也不担心算法。剩下的一个变量,就是密钥了。密钥的位数会变化吗?密钥的位数变化有影响吗?
一般来说,我们也不太关心密钥的位数变化,密钥少一位似乎也不是什么无关紧要的事情。所以,出于互操作性的考虑,很多标准和协议(包括应用最广泛的 TLS 1.2 协议)需要把密钥的高位的零清除掉,然后再参与运算。
原来 128 位的密钥,可能就被清除成了 127 位或者 126 位的密钥了。2018 年发布的的 TLS 1.3 版本,不再需要清除密钥高位的零。少一位密码,当然会带来计算性能的差异,以及由此引发的计算时间偏差。可是,似乎 2020 年之前,没有人担心这件事。
直到 2020 年 9 月 8 日,当我正在写这一篇稿的时候,一个名字叫做“浣熊攻击”的安全研究成果发布了。浣熊攻击可以利用密钥高位清零造成的运算时间差,通过观察、测算运算时间,运用统计学的技术破解运算密钥。这实在是一个了不起的发现。
目前来看,这种攻击方式还比较复杂,不容易执行。但是,一旦发现攻击方法,如果业界没有采取及时的措施,攻击技术的改进速度是惊人的。“浣熊攻击”出现,再一次敲了敲大门,警告我们要尽量避免计算时间偏差和计算算力偏差,谨慎地处理不可避免的计算时间偏差和算力偏差。
Take Away(今日收获)
今天,通过解构 CBC 模式,我们讨论了在分组运算里,一个典型的链接模式是什么样子的,以及重申了初始化向量的唯一性要求。使用唯一的初始化向量和恰当的链接模式,可以帮助我们防范数据重放攻击。
还有,通过异或运算和密钥位数的讨论,我们要小心计算时间偏差和计算算力偏差对算法安全性的影响。一般来说,这是一个特别容易忽视的问题。不仅仅是密码学算法,对所有私密数据的运算,都要小心处理计算时间偏差和计算算力偏差。否则,都有数据泄漏的危险。
另外,为了后面更进一步地讨论 CBC 模式的安全问题,我们还在这一次埋了不少的伏笔暗线,比如,初始化向量不需要保密,异或运算的特点等。
通过今天的讨论,我们要:
- 理解 CBC 模式的三个关键点。
- 了解计算时间偏差和算力偏差对算法安全性的影响。
思考题
今天的思考题,是一个动手题,也是一个简单的密码算法漏洞扫描的思路。
通过上面的讨论,我们知道密钥的位数很关键,一位也不能多,一位也不能少。找一个你熟悉的密码算法库,这个算法库可以是 Java Script 的,也可以是 Java 的,也可以是你熟悉的项目使用的算法库。
然后,调用它的对称密钥生成接口,试着产生很多 128 位的密钥。你看一看,有没有可能返回 127 位或者 129 位的密钥。如果你找到了不是 128 位的密钥,这个算法库就有潜在的安全问题。
如果你恰好学过统计学,还能使用统计学的软件,你可以试着多做一道思考题。我假设你知道 RSA 非对称密钥算法,也了解它的调用接口。同样的,找一个你熟悉的 RSA 算法实现,生成一对 1024 位 RSA 非对称密钥,用公钥加密大量的 1024 位的不同数据,然后用私钥解密这些数据,统计解密消耗的时间。
如果解密时间不是大致相同的,这个 RSA 实现就是有问题的。破解起来可能就是分分钟的事情。这是一个让我们了解计算时间偏差和计算算力偏差的练手题,也是个常见的分析 RSA 实现漏洞的攻击办法。
欢迎在留言区留言,记录、讨论你的发现。
好的,今天就这样,我们下次再聊。
文章作者 anonymous
上次更新 2024-01-30