12|朴素贝叶斯:让AI告诉你,航班延误险该不该买?
文章目录
你好,我是海丰。
今天,我们接着来讲一个基础的分类算法,朴素贝叶斯(NBM,Naive Bayesian Model),也可以简称 NB 算法。
你可能想说,贝叶斯我听过,什么叫朴素贝叶斯呢?其实,朴素贝叶斯就是我们在贝叶斯原理的基础上,预先假定了特征与特征之间的相互独立。那特征之间的相互独立是什么意思呢?简单来说,一个人的性别是女性和她是中国国籍这两项特征就是相互独立的,因为她的国籍不会影响到她的性别。那特征之间不相互独立也很好理解了,像是一个人的身高会影响他衣服的尺码,所以身高和衣服的尺码就不是相互独立的。
那特征与特征之间相互独立的好处是什么呢?朴素贝叶斯算法怎么解决分类问题呢?我们又该怎么使用它呢?今天,我们就通过一个预测购买航班延误险的例子,来给你详细讲一讲。
如何理解 朴素贝叶斯 算法?
有的同学可能对贝叶斯算法还不是非常熟悉,或者忘得差不多了,所以在讲朴素贝叶斯算法之前,我们先来说说贝叶斯算法以及相关的基础概念。
1. 贝叶斯的原理
贝叶斯是由一名英国数学家提出来的,贝叶斯就是这个数学家的名字。那它是干什么的呢?
比如说,我们拿到一个长得很大的西瓜,拍一拍它会有咚咚咚的声音,而且这个西瓜的价格还特别贵,那我们就觉得它应该挺甜。虽然这个西瓜不一定是甜的,但是这些经验可以帮助我们在一定概率下找到甜西瓜。
这就是贝叶斯的原理:当不知道这个事物实际情况的时候,我们可以根据一些相关的条件来判断这个事物的本质。与贝叶斯相关的基础概念有 3 个,分别是条件概率、先验概率、后验概率。
条件概率就是事件 B 在另一个事件 A 已经发生条件下的概率,记作 P(B|A)。在统计学中,也称之为似然函数。比如说,北京下雨后,发生道路堵车的概率。
先验概率是事件 A 或 事件 B 是根据经验来判断发生的概率,记作 P(A)、P(B)。比如说,今天我面试了某厂的员工,根据过去的经验这个公司来的员工都很优秀,所以我判断这个人大概率也很优秀。
后验概率是我们已经看到某个事情发生了,再判断这个事情发生原因的概率,即在事件已经发生后,推测原因。比如 P(A|B) 是已知 B 发生后 A 的条件概率,也叫做 A 的后验概率。比如说,我们知道一个西瓜很甜,这个西瓜很甜的原因可能是土壤好,光照充分等等。这个时候,一个西瓜很甜是因为它的土壤非常好的概率,就是后验概率。
实际上,贝叶斯的原理就是根据先验概率和条件概率估算得到后验概率。
2. 朴素贝叶斯的原理
朴素贝叶斯就是在贝叶斯的原理上,加了一个前提假设:所有的条件对结果都是独立发生作用的。这该怎么理解呢?
我们先来看朴素贝叶斯的公式:
P(A∣B)=P(B)P(B∣A)P(A)
你可能会说,看到公式我就头大。别着急,我们这就来快速理解一下这个公式。我们假设,公式里的 A 代表堵车,B 代表北京下雨,P 代表概率,所以我们可以得到这几个概率:
- P(A):堵车的概率,也就是事件 A 发生的概率;
- P(B):下雨的概率,也就是事件 B 发生的概率;
- P(B|A):在堵车的情况下,北京下雨的概率,也就是在 A 的情况下,发生 B 的概率;
- P(A|B):在北京下雨的情况下,堵车的概率,也就是在 B 的情况下,发生 A 的概率。
那朴素贝叶斯公式就可以理解成是在北京下雨的情况下,求堵车的概率。根据过往的统计结果,我们可以得到 P(A)=60%,P(B)=30%,P(B|A)=40%,根据公式:P(A|B)=P(B|A) P(A)/P(B) = 40% * 60% / 30% = 80%。也就是说,在北京下雨的情况下,有 80% 的可能性会堵车。
因此,在实际的应用中,朴素贝叶斯更适用于文本分类、情感分析、垃圾邮件分类这类场景,毕竟这些数据的相互独立性更高。另外,朴素贝叶斯还会和协同过滤一起,使用到推荐系统中。当然,在实际工作中,贝叶斯的应用会更加复杂。接下来,我就以售卖机票的场景下,是否增加延误险的需求为例,来给你讲讲它的应用。
朴素贝叶斯的应用案例
之前,国内的 OTA 行业(Online Travel Agency,在线旅行行业)基本都接入了延误险。业内的做法是在售卖机票的时候,直接搭售延误险,但这样的产品设计对于用户体验来说是有损害的,用户往往在不知情的情况下,购买了本不需要的产品。
这个时候,我们就可以通过预测航班是否可能延误,给用户提一个航班延误概率的提示,让用户自己做主是否有购买延误险。从平台角度来说,这既丰富了平台的产品,又提高了总体 GMV,从用户角度来说,这既不需要面对不存在的延误险和机票的捆绑销售,又有了更多的选择和参考。
那我们该怎么去判断航班是否可能延误呢?我们可以用朴素贝叶斯快速构建一个模型进行预测。具体的做法是这样的:我们已经知道,决定航班是否延误最主要的因素就是起飞地和降落地的天气情况。假设这些原因之间完全没有影响,那么我们可以去收集过去的飞行数据,计算出每一个条件,比如天气和飞机延误之间的关系。
假设,我们的用户正在浏览北京飞往深圳的航线,他坐飞机的时间段内,起飞地北京的天气是雪天,降落地深圳是雨天。
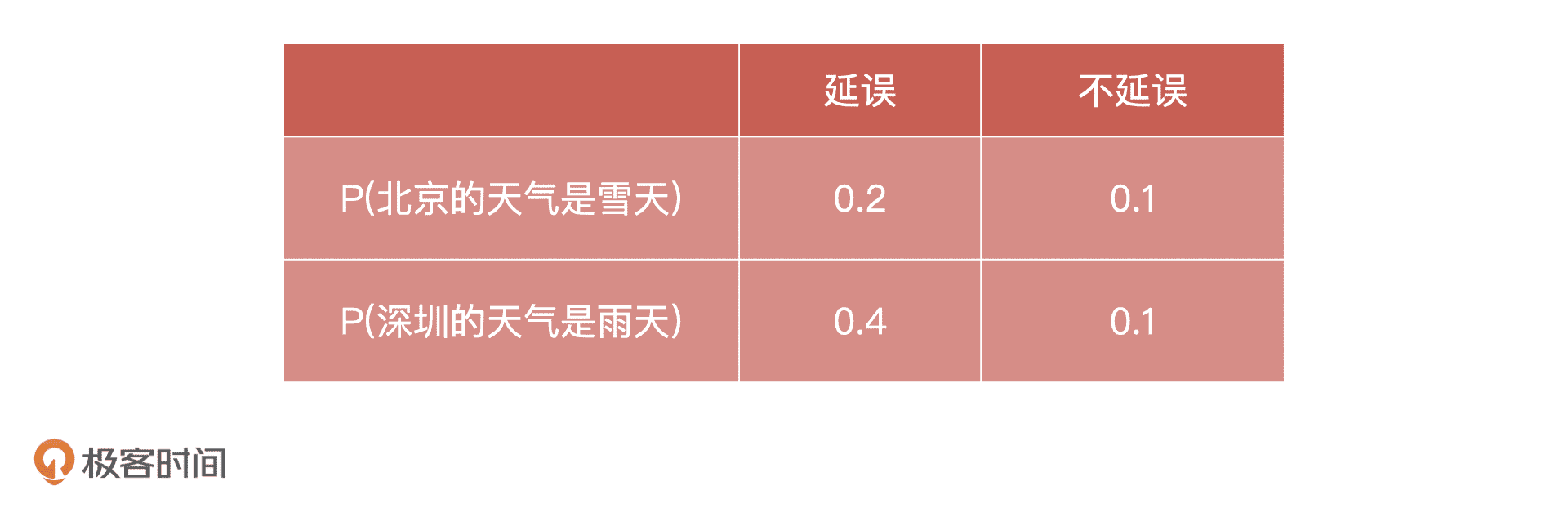
上面这些条件,我们给它们都分配一个代号。其中,北京的天气是雪天是 AI,深圳的天气是雨天是 A2,飞机延误的概率是 B1,不延误的概率是 B2。这样一来,我们就可以统计飞机延误和不延误情况下,北京是雪天和深圳是雨天的概率了。那么上面那些概率就可以变换为:
- 飞机延误的情况下,北京天气是雪天 = P(A1|B1) = 20%
- 飞机延误的情况下,深圳天气是雨天 = P(A2|B1) = 40%
- 飞机不延误的情况下,北京天气是雪天 = P(A1|B2) = 10%
- 飞机不延误的情况下,深圳天气是雨天 = P(A2|B2) = 10%
根据历史数据,我们可以得到总体延误的概率为 P(B1) = 30%,不延误的概率是 P(B2)= 70%。这个时候,根据我们之前讲的贝叶斯公式,就可以得到北京雪天同时深圳雨天的时候,飞机延误和不延误的概率了,具体公式如下所示。
- 飞机发生延误的概率是:P(B1|A1A2) = P(A1A2|B1) * P(B1) / P(A1A2)
- 飞机不发生延误的概率是:P(B2|A1A2) = P(A1A2|B2) * P(B2) / P(A1A2)
虽然这两个公式中的分母 P(A1A2) 我们不知道是多少,但我们直接比较分子就可以知道延误概率和不延误概率哪个更大。把具体的数值套入到公式中,我们就能得到发生延误的概率是 24%,不发生延误的概率是 7%,计算公式如下:
- P(A1|B1) * P(A2|B1)*P(B1)/P(A1)*P(A2) = 20% * 40% * 30% = 24%
- P(A1|B2) * P(A2|B2)*P(B2)/P(A1)*P(A2) = 10% * 10% * 70% = 7%
这样一来,当用户在浏览这个航线的时候,我们就可以提示用户,“该航线大概率会延误,请您按需购买延误险”。
朴素贝叶斯的优缺点
朴素贝叶斯的优点主要有两个,首先是算法的逻辑简单,因为它的核心就是贝叶斯公式,所以它实现的过程是不需要训练的,算法计算的时候对资源也占用比较小。
因此,当公司没有算法工程师的情况下,如果你想做一些相对简单并且条件比较独立的事件预测时,你完全可以对研发工程师提出这样的要求:由你来提供相应的条件,研发工程师通过公式来帮你预测结果。
这个时候,你不只是一个需求提出方,还是一个解决方案架构师,能够推动一个需求从 0 到 1 的落地,同时还不需要公司提供额外的资源,这就是你价值的体现。
但是由于朴素贝叶斯有一个假设前提,就是各个条件之间相互独立,互不影响。这让它的使用非常有局限性,只有在条件比较少,并且相互独立的时候,朴素贝叶斯的效果才会比较好。可是,现实世界中这种情况往往不存在,所以在面对条件个数比较多,或者条件之间有一些相关性的时候,朴素贝叶斯得到的效果就会差很多。
总结
今天,我带你一起学习了第三个分类算法,朴素贝叶斯。作为产品经理,我们首先要记住,这个算法的核心来自于贝叶斯公式,算法的前提假设是,算法中各个条件相互独立、互不影响。
同时,为了帮助你加深理解,我也把它的原理和基础概念总结在了下面的表格里。

接着,我们要重点掌握朴素贝叶斯的应用场景,我从两个方面帮你做了总结。
从算法适合的场景上来说,朴素贝叶斯比较适合用于垃圾邮件分类,用户情感预测这些和文本处理相关的场景,这些场景中,算法依赖的条件相互之间比较独立,所以适合用朴素贝叶斯算法来做。
从算法开发成本上来说,朴素贝叶斯适合项目周期比较紧张,算力资源不太充足的情况,因为朴素贝叶斯模型相对简单,构建过程不会太复杂,占用时间相对比较短,并且由于其相对简单的特点,对于算力的要求也不会太高。
课后讨论
假设,我们业务方 HR 团队希望你分析每一个员工的离职概率,你觉得用朴素贝叶斯合不合适?为什么?
欢迎在留言区写下你的思考和疑惑,也欢迎你把这节课分享给你的朋友,我们下节课见!
文章作者 anonymous
上次更新 2024-04-11