虽然异或问题成为感知器和早期神经网络的阿喀琉斯之踵，但它并非无解的问题。恰恰相反，解决它的思路相当简单，就是将单层感知器变成多层感知器。下图就是一个多层感知器的实例，这个包含单个隐藏层的神经网络能够完美地解决异或问题。

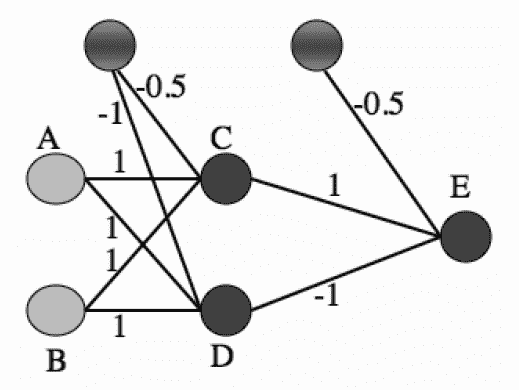（图片来自_Machine Learning: An Algorithmic Perspective_, 2nd Edition, Figure 4.2）

假定两个输入节点 A 和 B 的二进制输入分别为 1 和 0，则根据图中的权重系数可以计算出神经元 C 的输入为 0.5，而神经元 D 的输入为 0。在由 C 和 D 构成的隐藏层中，由于 C 的输入大于 0，因而符号函数使其输出为 1；由于 D 的输入等于 0，符号函数则使其输出为 0。在输出节点的神经元 E 上，各路输入线性组合的结果为 0.5，因而 E 的输出，也是神经网络整体的输出，为 1，与两个输入的异或相等。在此基础上可以进一步证明，这个神经网络的运算规则就是异或操作的运算规则。

多层感知器（multilayer perceptron）包含一个或多个在输入节点和输出节点之间的隐藏层（hidden layer），除了输入节点外，每个节点都是使用非线性激活函数的神经元。而在不同层之间，多层感知器具有全连接性，即任意层中的每个神经元都与它前一层中的所有神经元或者节点相连接，连接的强度由网络中的权重系数决定。多层感知器是一类前馈人工神经网络（feedforward neural network）。网络中每一层神经元的输出都指向输出方向，也就是向前馈送到下一层，直到获得整个网络的输出为止。

多层感知器的训练包括以下步骤：首先确定给定输入和当前权重下的输出，再将输出和真实值相减得到误差函数，最后根据误差函数更新权重。在训练过程中，虽然信号的流向是输出方向，但计算出的误差函数和信号传播的方向相反，也就是向输入方向传播的，正因如此，这种学习方式得名反向传播（backpropagation）。反向传播算法通过求解误差函数关于每个权重系数的偏导数，以此使误差最小化来训练整个网络。

在反向传播算法中，首先要明确误差函数的形式。当多层感知器具有多个输出时，每个分类结果 yjyj