37__全栈开发中的算法(下)
文章目录
你好,我是四火。
今天,我们来继续学习一些全栈开发中影响深远的算法,我们这次的归类是无损压缩算法。无损压缩,顾名思义就是经过压缩以后,数据的大小降下来了,但是只要经过还原,原始数据是一点都不丢失的。和无损压缩对应的,显然就叫做“有损压缩”了,它们能够做到在牺牲一定程度原数据质量的基础上,比有损压缩获得额外的压缩比。
无损压缩的算法其实有很多,但无论是哪一种,里面都没有多么神奇的把戏,**它们的最基本原理都是一致的,就是利用数据的重复性(冗余性)。**在经过某种无损压缩以后,由于数据的重复性已经降下来了,因此再压缩就无法获益了。
哈夫曼编码
不管是在哪一本系统介绍压缩算法的书中,那么多的无损压缩算法,哈夫曼编码(Huffman Coding)基本都是需要我们最先接触学习的那一个。哈夫曼编码从原理上看,它会根据字符的出现频率,来决定使用怎样的编码方式,并且是变长编码的一种。相应地,程序员熟悉的 ASCII 码,就是定长编码,因为总共就 128 个字符,不管是哪一个字符,占用的长度都是一样的。
下面我们来看一下哈夫曼编码的大致过程:
首先,统计被加密数据中每个字符出现的频率,把它们从高到低排好。比如下面这个表,就是某一段文字的字母出现的次数统计表格,你可以看到这些字母出现的次数是从左到右依次增加的:

接下去,我们就可以从表格的左侧开始取数据,并自下而上地构造哈夫曼树了。
我们每次只考虑表格中“出现次数”最少的两列。第一次,我们发现出现次数最少的是字母 h,其次是 f,因此分别构造最底层的两个叶子节点 h 和 f,并将它们的和 5 + 6 = 11 也求出来,构造成为它们的父节点:

同时,我们更新这个统计表格,使用这个父节点去代替它原本的两个节点 h 和 f,依然保持各列按照出现次数递增排列:

继续按照上面的操作,现在值最小的两个节点,分别为 7 和 8,因此现在这张图变成了:

而表格变成了:

继续,现在值最小的两个节点,分别对应 11 和 15:
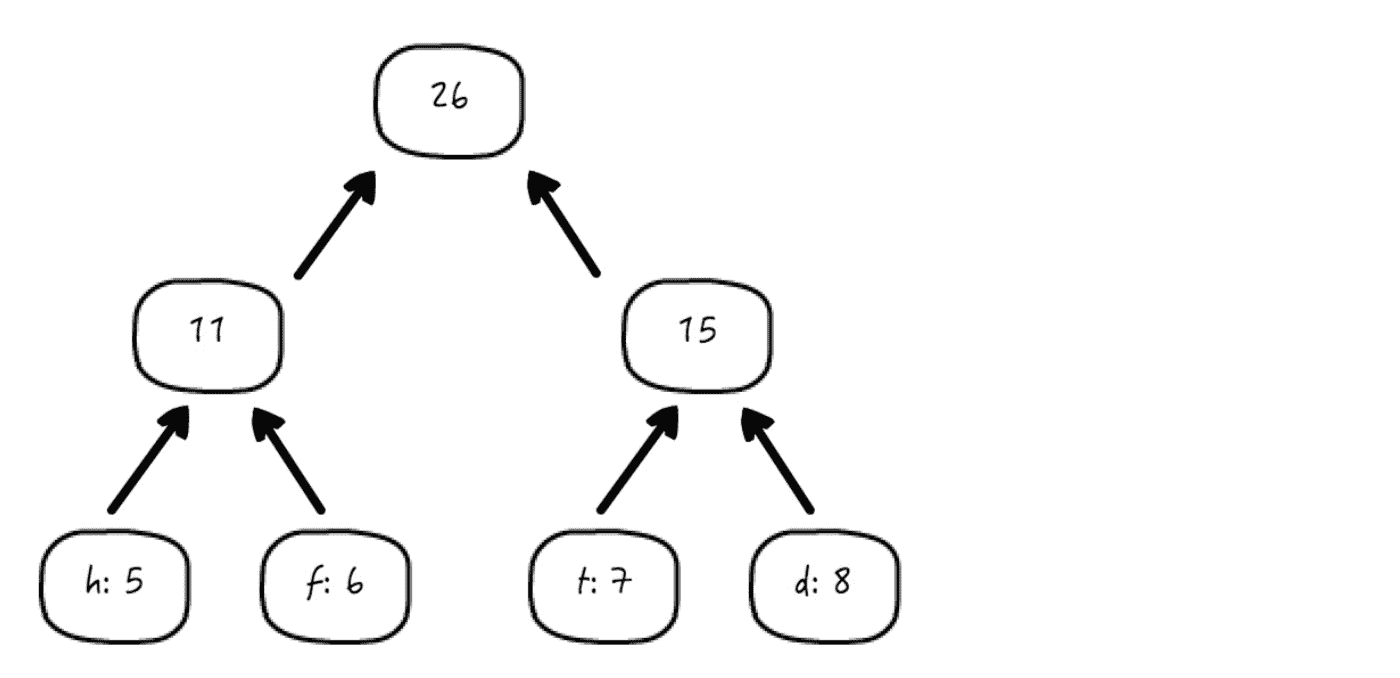
表格变成了:

继续:

表格只有两列数据了:

好,这棵树构造完成,这时候表格里只剩下一列了,即 e+a+h+f+t+d=76,我就不列出来了。在树构造完成后,我们给图中所有的左分支赋值 0,右分支赋值 1:
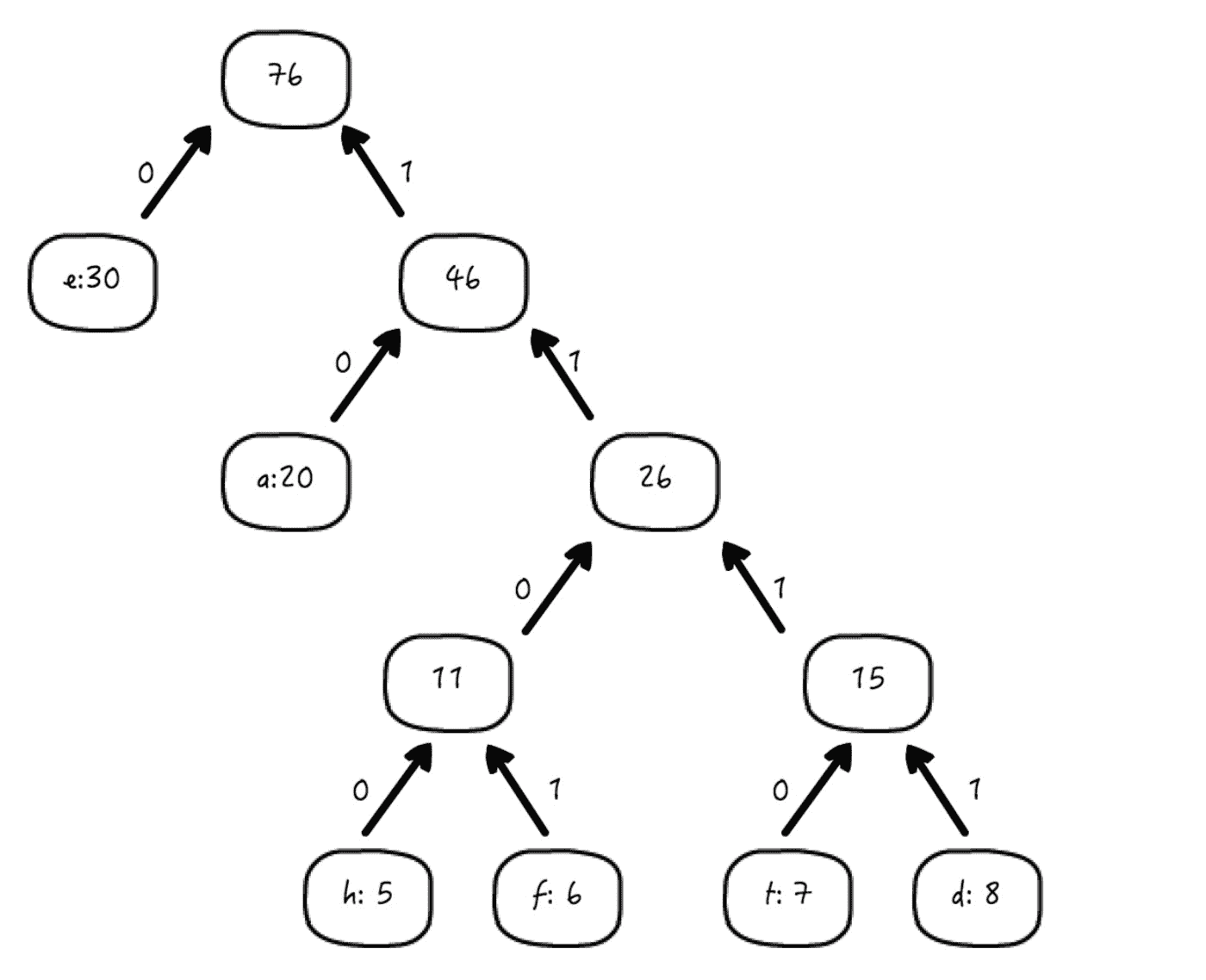
这就是哈夫曼树。
你可以看到,每一个叶子节点,都代表了我们希望加密的字符。**只要从根部开始,往叶子节点的方向按照最短路径的方式遍历(图中箭头的逆向),每一条路径都对应了实际的哈夫曼编码。**按照这个规则,让我们给最开始的那个记录字符出现次数的表格加上一行:

你可以看到,大致的规律是,出现频率越高的字符,编码串的长度就越短。如果有一个单词 date,它的编码就是:

这就是哈夫曼编码的原理,但是由于哈夫曼编码是变长的,为了解码端能够准确地解码,就需要编码端同时附上字母到编码的映射关系表(就是上面那个表格,出现次数一行可以删掉,剩下两行保留),也就是所谓的“编码表”。
RLE 编码
RLE 编码,即 Run-Length Encoding,是一种原理非常简单的压缩编码方式,它利用的就是字符的“简单重复”。并且有意思的是,这种编码方式和很多其它压缩编码方式不冲突,也就是说,数据可以以特定的方式经过 RLE 编码后,再使用哈夫曼等其它方式进一步压缩编码。
举个例子,如果有这样一段单个字符重复率比较高的原串:
AAAAABBCDDDDDDD
它就可以使用 RLE 的方式编码成:
5A2B1C7D
这表示这段原数据中有 5 个连续的 A,2 个连续的 B,1 个 C 和 7 个连续的 D。
这种方式下,不知你是否想到,也可能存在问题。比如说,如果连续字符重复的比率很低,像是这样一段字符:
ABCDABCD
按照刚才的规则,它就会被编码成:
1A1B1C1D1A1B1C1D
什么嘛,编码后居然比原字符串还长!
**因此,RLE 这种压缩编码方式,更适合于连续字符发生率较高的数据。**比方说黑白的栅格图像(关于栅格图像的概念,你可以参考 [第 18 讲]),里面往往存在着大片大片的重复字符。
算术编码
算术编码,即 Arithmetic Coding,我们可以拿它和哈夫曼编码比较起来看:二者都会根据字符的出现频率来设定编码规则,但哈夫曼编码针对的单位是单个字符,每个字符对应一个数;而算术编码,则是整个消息串(编码单元)编码成一个数。
举个例子,某数据可能由四个字母组成,每个字母出现的概率如下:

根据上面的统计,假如说现在我们要给单词 eat 来进行算术编码。
第一步:我们先把 0 到 1 的范围按照该比例划分成这样 4 个区域,第一个字母 e 就在从 60% 到 100% 的位置(每一个区域,都是左闭右开的区间,比如 t 的区间是 [0, 10%))。

第二步:接下来是字母 a,我们把上面 e 这个区域,即 [60%, 100%),按照同样的比例划分成 4 个区域,根据同样的计算,a 的位置在 72% 到 84% 这一段上。

第三步:最后是字母 t,做法也依然如此,把上面 a 这个区域按照同一比例划分成 4 个 区域,t 的位置在 72% 到 73.2% 这一段区域内。

那么,我们就可以给它取 73%,因为它就在最后的区域 t 内,当然,在编码中我们可以去掉百分号。因此,基于上面的统计,eat 这个单词,就可以采用算术编码成数值 73。也就是说,通过这种方法,一段编码前的数据,最后编码成了一个数。
这就是算术编码的大致原理,根据已知的统计,将给定数据段进行划分,原则就是让出现概率较大的字符根据比例来分配到相对更大的数据段,解码方根据编码方提供的这一依赖统计数据,就可以做出准确的解码。
当然,上面作为一个示例,是做了相当的简化了的,在实际应用中,还有很多因素需要我们考虑,比如:
1. 采用二进制来代替十进制
我们使用十进制,仅仅是示例之用,为了便于让你理解。实际上,使用二进制可以减小“浪费”的字符,从而缩短编码后的长度,提高压缩比。我们还是拿上面的那个例子来说,72% 和 73% 在数值位数长度相同的情况下都可以表示 eat 这个词,这就是一定程度上的浪费。最理想的状况,应当是用于压缩后数据表达的数值,可以按照比例“恰好”地去覆盖所有被编码的数据组合——而不存在某一种表达是冗余的,或者说对应的被编码的实际数据组合不存在。
2. 引入结束字符
通常我们不会把整个输入完全使用一个编码数值来表示,而是将输入根据某种规则划分成若干个部分,分别采用算术编码处理。比如一段英文文字,就可以使用空格来标识每一个单词的结束,因此像空格这样的“结束符”需要考虑到编码字符内。
3. 适当考虑条件概率
你看,上面例子中的第一步、第二步和第三步,t、d、a、e 的分布都是一样的,但是实际上,这个分布在“前一个”字母确定的情况下,是可以有变化的。举个例子,前面提到的字母概率分布,在“前一个字母为 t”的前提下,当前字母的概率遵循如下表格:

你可以看到,这个条件下的统计和前文比,发生了明显的变化,我们说它是“1 级”条件概率。如果我们讨论,在前两个字母分别是 t 和 e 的前提下,接着看第三个字母的概率分布,这时的条件概率其实就到“2 级”了。
你也可以想象,由于排列组合的关系,我们不可能无限地考虑条件概率,考虑 n 级条件概率,这个编码表的大小就是最初编码表大小的 n 次方,因此条件概率的选择,我们要么选择某几个特定字母(规则)的条件概率,比如我们只考虑字母 t 和字母 d 的条件概率;要么严格限制条件概率的级数,比如就实现 1 或 2 级的条件概率。
4. 将静态模型改进为自适应模型
算术编码需要在统计数据的指导下进行,我们当然希望统计数据可以精确。我们的例子中,统计信息是预先确定的,即什么字母的出现概率是百分之几都是已经知道的。也就是说,我们应用的是“静态模型”,对于静态模型来说,我们可以相对容易地追求最佳的压缩比。
但是在实际应用中,很多时候我们是不知道这个的,或者说,即便知道,这个值也是在不断变化的。使用静态模型的问题也就在这里,如果用一个静态的统计去指导一个动态变化的问题,就像刻舟求剑一样,哪怕一开始编码是高效的,很快这个压缩率就降下来了。
因此我们经常需要把静态模型变成自适应模型。如果还是前面那个例子显示的四个字母,假如说在一开始的时候,这些字母将在待编码的数据中出现的概率是未知的,那么我们可以简单地认为“每个字母都已经出现了 1 次”:

那么,随着我们的编码流程向下进行,每次编码,或者每几次编码前这个概率统计,就会根据当前情况得到更新,再来指导下面的编码,不过算法和前面保持不变。
比如读入第一个字符 e 以后,这个统计表格就变成了:

再读入一个字符 a,这个统计表格就变成了:

你看,随着编码的不断进行,这个统计表格会不断自我修正。如果源数据的字母分布在数据量增大的时候是收敛的,即不断趋近于某一个相应的比例,那么这个统计也会不断接近它,因此随着时间的流逝,压缩工作的进行,压缩的效果会越来越好。
**但是,在很多实际的场景中,这个分布统计并不是收敛的,而是随着时间的流逝会不断变化的。**举例来说,视频直播,随着播放的进行,统计数据需要时不时地发起更新,因为视频在不断变化,某一时间段内重复率高的数据串,可能到了下一个时间段内就变了。这时候,对于统计数据的生成就值得做文章了,比如我们可以选取一个适当的时间权重,越是新的数据,权重越大,这种情况下我们得到的统计就具有一定的即时性了,而一些较老的数据,显然对于统计分布的影响就很小了,而老到一定程度的数据,甚至就直接忽略掉好了。
于是,通过这种方式,统计数据不断地随着实际数据流的变化而变化,那么编码的规则(编码表)就可以实现不断地自我调整,去适应数据的变化,这也是一些视频流编码都采用自适应模型的原因。
好,现在我们回过头来看看哈夫曼编码和算术编码,它们尽管在技术实现上有着诸多不同,但是它们的压缩过程,都包含了这样两个步骤,这也是大部分时候我们使用的压缩算法实际上所遵循的两个步骤:
- 第一步,分析并计算得到原始数据的统计模型;
- 第二步,根据统计模型,将相对较多出现的数据用较短的编码串表示,而较少出现的数据用较长的编码串表示。
总结思考
今天我们学习了无损压缩算法中较为基础的几种,事实上,对于我们日常接触的那些实际的、商用的压缩算法,往往都是这些基础技术的综合使用。好,希望你已经理解了这些算法的本。
现在又到了提问时间:
- 对比哈夫曼编码和算术编码,你能否比较并分别说出二者的优劣?
- 关于哈夫曼编码,如果编码后的串,其中的某个数值(无论是 0 还是 1)丢失了,你觉得这样的数据损坏,会导致多大比例的数据无法被正确解码?
你可以回想一下上一讲的选修课堂,和本讲一样,都是将原数据进行某种特定的编码以后,得到目标数据,但是二者的目的是截然不同的,前者是为了加密,保护原始信息不被泄露、不被篡改,而后者是为了压缩,减少存储和传输数据的大小。
好,今天就到这里,不知道你是否在全栈开发的算法学习后有所收获,欢迎你和我分享你的思考。
扩展阅读
- 今天我介绍了几个较为基础和经典的无损压缩算法,你可以在这里查看无损压缩的其它算法。就如同软件开发没有银弹一样,不同的无损压缩算法擅长于不同的数据类型和特定的数据重复模式,没有一种通用的方法可以对所有的数据压缩都做到最好。
- 对于哈夫曼树的生成,这里有一个网站,可以根据你输入的字符串,图形化地展示哈夫曼树。
- 这两讲我介绍了一些全栈开发中重要的算法,但是还有许多其它很有意思、也很有地位的算法,推荐你阅读 InfoQ 上的这篇译文——计算机科学中最重要的 32 个算法。

文章作者
上次更新 2025-01-03