22_模型稳定性评估:如何用PSI来评估信用评分产品的稳定性?
文章目录
你好,我是海丰。
模型稳定性指的是模型性能的稳定程度,只有稳定性足够好的模型才能通过上线前的评估,而且上线后,我们也要对模型稳定性进行观测,判断模型是否需要迭代。在实际工作中,我们会用 PSI 来评估模型的稳定性。
这节课,我们就借助一个信用评分的产品,来详细说一说 PSI 是什么,它该怎么计算,以及它的评估标准。
案例:客群变化对模型稳定性的影响
在金融风控领域,稳定性对于风控模型来说就是压倒一切的条件。模型只有足够稳定,才能既通过上线前层层的验证和审批,又能在上线后运行足够长的时间。但在实际工作中,像客群变化这类无法避免的情况,往往会直接影响模型的稳定性。
比如说,在模型上线时候,前端流量有 5000 的测试用户,模型输出的分布可能是下面这样的。如果业务设置阈值为 60 分,那么,60 分以下的人我们会拒绝放款。这样一来,模型会拒绝掉大概 20% 的人,这种情况对于业务来说是可以接受的。
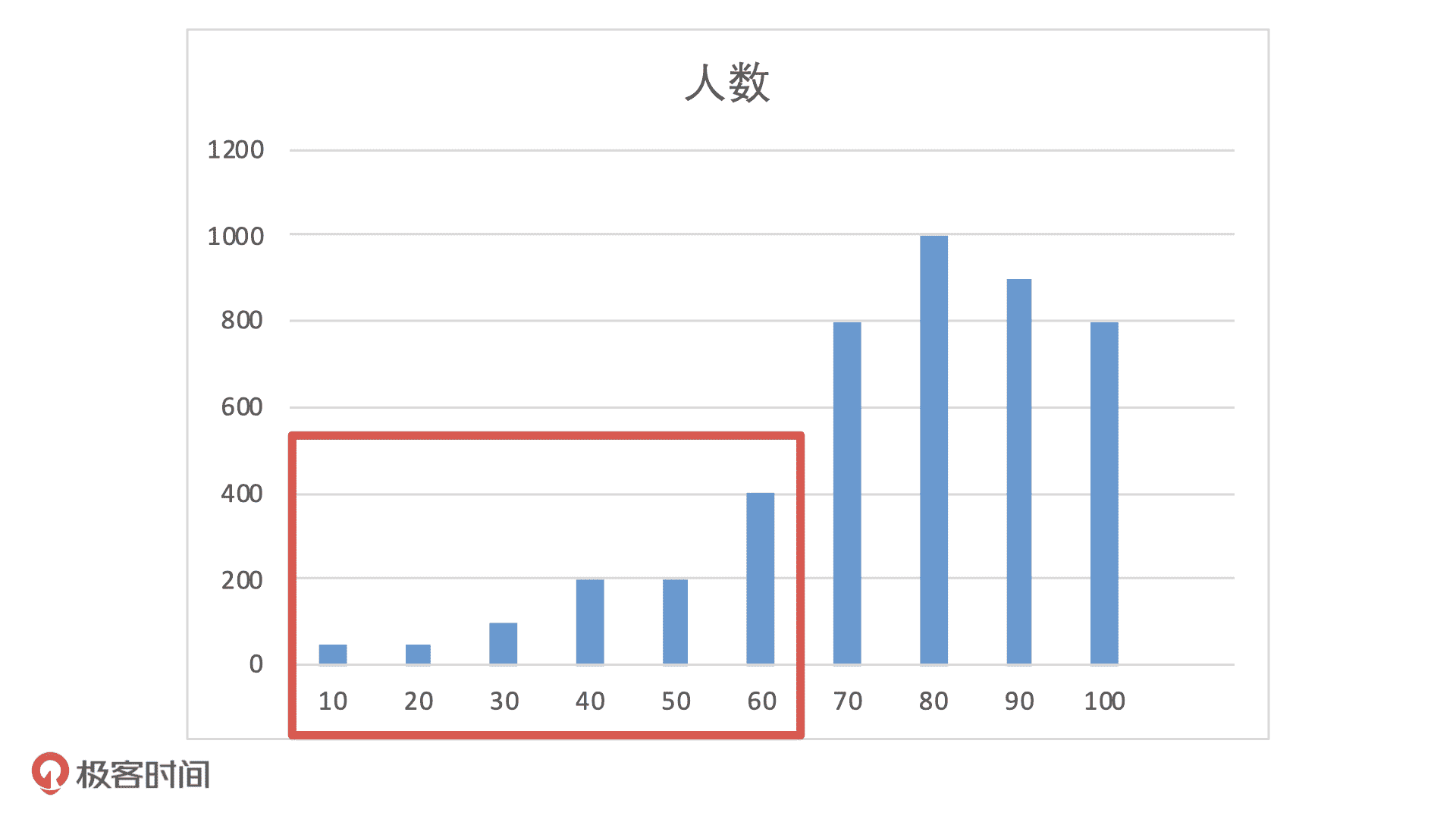
如果模型上线后,前端流量没有发生变化,还是 5000 个待测用户,但是客群发生了变化,从测试用户变成了线上的用户。这个时候,模型输出的分布就会变成下面这样。

如果我们还是用 60 作为阈值,模型就会拒绝掉 50% 的用户。当前市场下,前端流量这么贵,如果风控拒绝了 50% 的用户申请,估计市场或者运营的同学,肯定不会放过风控部门了。
在实际工作中,这种情况的发生就是因为模型不稳定。为了避免这种情况的发生,我们必须要在上线前对模型的稳定性进行评估,尤其是在类似金融风控这类对模型稳定性要求高的场景中。
那么,在上线前,我们该怎么使用 PSI 对模型稳定性进行评估呢?
PSI 指标该如何计算?
首先,我们来看看 PSI 是什么。
所谓 PSI 指标就是群体稳定性指数(Population Stability Index),通过 PSI 指标,我们可以得到不同样本(不同时间段给到模型的样本)下,模型在各分数段分布的稳定性。
PSI 的计算公式
我们知道,稳定性是一个相对的概念,只有通过对比,我们才能知道模型是不是稳定。所以,想要计算模型的稳定性,我们需要先有一个参照物。在信用评分模型中,为了进行对比,我们至少需要两个分布结果,一个是预期分布结果一个是实际分布结果。
在产品验收阶段,我会使用模型上线时的 OOT 样本作为预期样本,非 OOT 时段的近期抽样样本作为实际样本。不仅产品经理,算法工程师也需要对模型的稳定性进行评估,他们通常会在模型验收之前,使用验证样本作为实际分布,使用训练样本作为预期分布,这一点你知道就可以了。
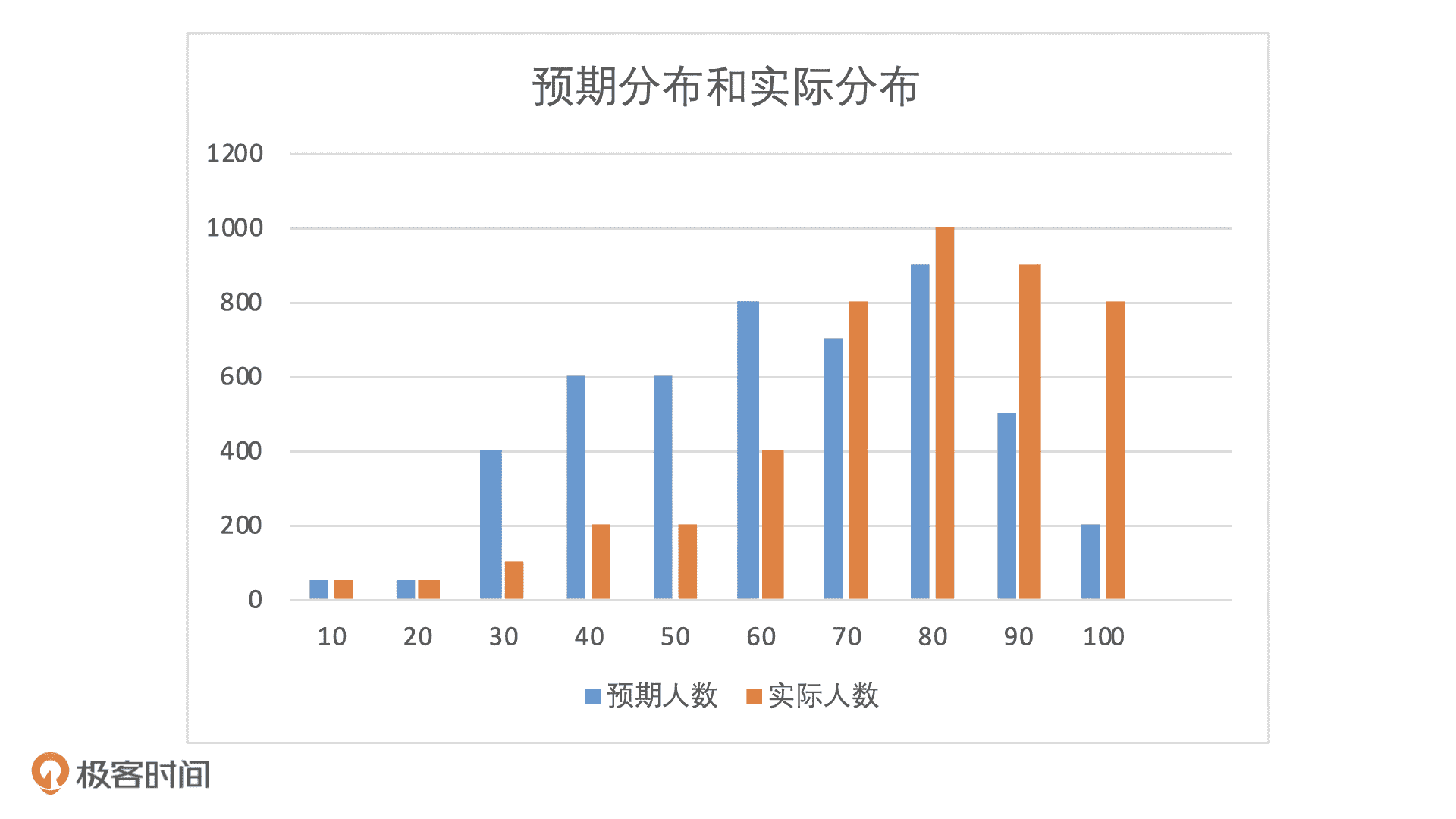
我们期望的是,模型在遇到不同时间段样本的时候,每个分数段的人群占比不要发生太大变化。为了更直观看到预期分布和实际分布的这种变化,我们可以把人数分布直接转化为占比分布。

通过这张图,我们肉眼就可以看到,在这个模型中,两个不同人群的占比发生了很大的变化。那么,我们该怎么去量化这个变化呢?这个时候就需要用到 PSI 指标了,它的公式是:PSI = SUM ( 实际占比 - 预期占比 ) * ln ( 实际占比 / 预期占比 )。
已知,这个信用评分产品的分数范围是 [0, 100],分数越高说明用户的信用越好。接下来,我们来计算一下这个信用评分产品的 PSI。具体来说,我们可以分三步来操作,分别是分箱、计算实际分布、计算 PSI 数值。
第一步:分箱
由于信用分数是一个个连续值,实际操作中我们不可能对每一个分数点进行测试,因此,我们需要将变量的预期分布进行分箱操作,然后统计每个分箱里面样本的占比。分箱的方式有两种,一种是等频分箱,另一种是等距分箱。分箱方式不同,模型计算的结果也会有略微的差异。
那么,什么是等频分箱和等距分箱呢?所谓等频分箱是指每个分箱中的样本数量相等,分数段不同,并且分数段是根据人数占比计算得到的。比如,对于把信用评分的结果,我们使用等频分箱的方式可以把它们分为 10 个箱子。其中,每个箱子分数段不同,但是里面的人数相同,示例如下:

等距分箱指的是每个分箱中分数段相同,人数不同,人数是按照分数平均切分的。比如说,对于信用评分结果,我们使用等距分箱把它也分为 10 个箱子,那每个箱子中的分数段相同,但是里面的人数不同,大致样例如下:

因为 PSI 看的是分数段中人数波动情况,所以这里我们选择对预期分布进行等距分箱,也就是上面的分箱方式。
第二步:计算实际分布
我们知道,PSI 比较的是预期分布和实际分布,而模型上线前我们就已经有了预期分布(我习惯使用算法进行 OOT 测试时候得到模型分布数据,当然你也可以选择其他样本作为预期分布),并且我们也已经对数据完成了分箱。接下来,我们需要选择进行测试的样本,把样本传入模型得到实际测试结果,即所有测试用户的信用分数。然后,我们再根据上一步选择的分箱方式,将实际测试结果同样进行分箱,计算分箱后的占比。一般来说,测试样本距离当前日期越近越好。

第三步:计算 PSI
完成分箱,计算出实际分布之后,我们就可以利用公式计算 PSI 了。为了方便计算和查看,我们将前两步的结果整合到一张表格中。

以第一行的分数段 [0,10] 为例,我们先计算实际占比 - 预期占比 = 1.5%-2% = -0.5%,然后计算实际占比 / 预期占比 = 1.5% / 2% = 75%,之后计算 ln ( 实际占比 / 预期占比) = -0.28768。最后是计算 index = ( 实际占比 - 预期占比 ) * ln ( 实际占比 / 预期占比 ) = -0.5% * -0.28768 = 0.0014。
接下来,我们分别计算其余 9 组分箱的 index 值,最后可以得到下表的数据:

根据公式,最终的 PSI 值就是表格每一个分箱的 index 求和:PSI=sum(index1+index2+…+index10) = 0.0127。
以上就是 PSI 指标的计算过程了。但是,得到 PSI 之后,我们怎么利用它对模型稳定性进行评估呢?我们得到的数字又代表什么业务含义呢?
在业务层面,PSI 数值越小说明两个分布之间的差异也就越小,也就代表模型越稳定。更具体一点,我们一般会这么定义模型的稳定性:

小结
PSI 的计算过程非常简单,在工作中我们也不需要手工去计算 PSI,通过 Python 代码就可以直接计算。今天,我希望你能通过它的计算过程深入理解它的原理。
首先,PSI 指的是群体稳定性指数,它可以表示不同样本下模型的稳定性。稳定性是一个相对的概念,在信用模型中,我们会使用至少两类分布结果进行判断,分别是预期分布结果和实际分布结果。这其中,计算 PSI 的目的,就是为了判断实际分布和预期分布相比是否存在比较大的变化。
那在实际计算 PSI 的时候,我们会通过三步来进行,分别是分箱、计算实际分布和计算 PSI。其中,分箱是一个非常常见和重要概念,不仅是在计算 PSI 的时候,在对其他指标进行评估的时候,我们也会借助分箱的方式,来帮助我们处理数据。
至于利用 PSI 对模型进行评估就非常简单了,总的来说就是 PSI 数值越小,两个分布之间的差异也就越小,模型越稳定。PSI 的值在 0.1-0.25 之间,都是可以接受的范围。
除此之外,在实际工作中使用 PSI 的时候,我还有 3 点建议提供给你。
- PSI 值不应该只是在模型上线时候关注,在上线后我们也要持续关注。因为客群必然会随着时间的推移发生变化,这会导致人群分布发生变化,而且这个变化会越来越大,从而影响模型的预测能力。
- 影响 PSI 的变化因素很多,常见的有客群变化(尤其是互金市场用户群体变化很快)、数据源变化(外部接入的数据源停用或者效果下降)等等。
- 上线后,为了能够随时关注模型稳定性的情况,我建议你根据业务场景对模型稳定性的要求,对模型 PSI 进行按日、按月或者按季度监控。
课后讨论
今天的最后,我还想请你思考一个问题,我们今天说了 PSI 指标是为了衡量两个分布之间的差异,它的公式是:SUM ( 实际占比 - 预期占比 ) * ln ( 实际占比 / 预期占比 ) 。那么,为什么公式需要增加“ln ( 实际占比 / 预期占比 ) ”部分,而不是直接使用:SUM ( 实际占比 - 预期占比 ) 呢?
期待在留言区看到你的思考和答案,我们下节课见!
文章作者
上次更新 2025-01-03