【MAB问题】结合上下文信息的Bandit算法
文章目录
上一篇文章我说到,Bandit 算法用的是一种走一步看一步的思路,这一点看上去非常佛系,似乎一点都不如机器学习深度学习那样厚德载物,但是且慢下结论,先看看我在前面介绍的那几个 Bandit 算法。
UCB 回顾
这些 Bandit 算法,都有一个特点:完全没有使用候选臂的特征信息。特征可是机器学习的核心要素,也是机器学习泛化推广的依赖要素。
没有使用特征信息的 Bandit 算法,问题就在于只能对当前已有的这些候选臂进行选择,对于新加入的候选只能从 0 开始积累数据,而不能借助已有的候选泛化作用。
举个例子,假如有一个用户是鹿晗的粉丝,通过 Bandit 算法有两个鹿晗的广告得到展示,并得到了较好的收益。
那么对于一个新的广告,如果具有鹿晗这个特征,直觉上前两个鹿晗广告的收益信息可以泛化到当前新广告上,新广告就不是完全从 0 开始积累数据,而是有了一定的基础,这样的收敛会更快。
UCB 和汤普森采样这两个 Bandit 算法在实际中表现很好。于是,前辈们就决定送 UCB 去深造一下,让它能够从候选臂的特征信息中学到一些知识。
UCB 就是置信上边界的简称,所以 UCB 这个名字就反映了它的全部思想。置信区间可以简单直观地理解为不确定性的程度,区间越宽,越不确定,反之就很确定。
- 每个候选的回报均值都有个置信区间,随着试验次数增加,置信区间会变窄,相当于逐渐确定了到底回报丰厚还是可怜。
- 每次选择前,都根据已经试验的结果重新估计每个候选的均值及置信区间。
- 选择置信区间上界最大的那个候选。
“选择置信区间上界最大的那个候选”,这句话反映了几个意思:
- 如果候选的收益置信区间很宽,相当于被选次数很少,还不确定,那么它会倾向于被多次选择,这个是算法冒风险的部分;
- 如果候选的置信区间很窄,相当于被选次数很多,比较确定其好坏了,那么均值大的倾向于被多次选择,这个是算法保守稳妥的部分;
- UCB 是一种乐观冒险的算法,它每次选择前根据置信区间上界排序,反之如果是悲观保守的做法,可以选择置信区间下界排序。
LinUCB
“Yahoo!”的科学家们在 2010 年基于 UCB 提出了 LinUCB 算法,它和传统的 UCB 算法相比,最大的改进就是加入了特征信息,每次估算每个候选的置信区间,不再仅仅是根据实验,而是根据特征信息来估算,这一点就非常的“机器学习”了。
在广告推荐领域,每一个选择的样本,由用户和物品一起构成,用户特征,物品特征,其他上下文特征共同表示出这个选择,把这些特征用来估计这个选择的预期收益和预期收益的置信区间,就是 LinUCB 要做的事情。
LinUCB 算法做了一个假设:一个物品被选择后推送给一个用户,其收益和特征之间呈线性关系。在具体原理上,LinUCB 有一个简单版本以及一个高级版本。简单版本其实就是让每一个候选臂之间完全互相无关,参数不共享。高级版本就是候选臂之间共享一部分参数。
先从简单版本讲起。
还是举个例子,假设现在两个用户,用户有一个特征就是性别,性别特征有两个维度,男,女。现在有四个商品要推荐给这两个用户,示意如下。
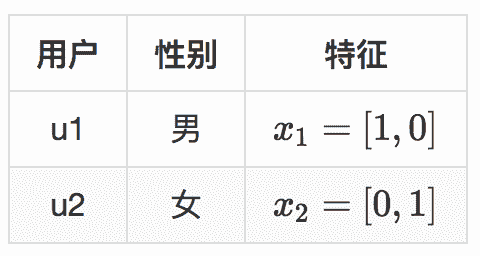
两个用户就是 Bandit 算法要面对的上下文,表示成特征就是下面的样子。

每一次推荐时,用特征和每一个候选臂的参数去预估它的预期收益和置信区间。
xi×θjxi×θj
文章作者
上次更新 2025-01-03