43__拓扑排序:如何确定代码源文件的编译依赖关系?
文章目录
从今天开始,我们就进入了专栏的高级篇。相对基础篇,高级篇涉及的知识点,都比较零散,不是太系统。所以,我会围绕一个实际软件开发的问题,在阐述具体解决方法的过程中,将涉及的知识点给你详细讲解出来。
所以,相较于基础篇“开篇问题 - 知识讲解 - 回答开篇 - 总结 - 课后思考”这样的文章结构,高级篇我稍作了些改变,大致分为这样几个部分:“问题阐述 - 算法解析 - 总结引申 - 课后思考”。
好了,现在,我们就进入高级篇的第一节,如何确定代码源文件的编译依赖关系?
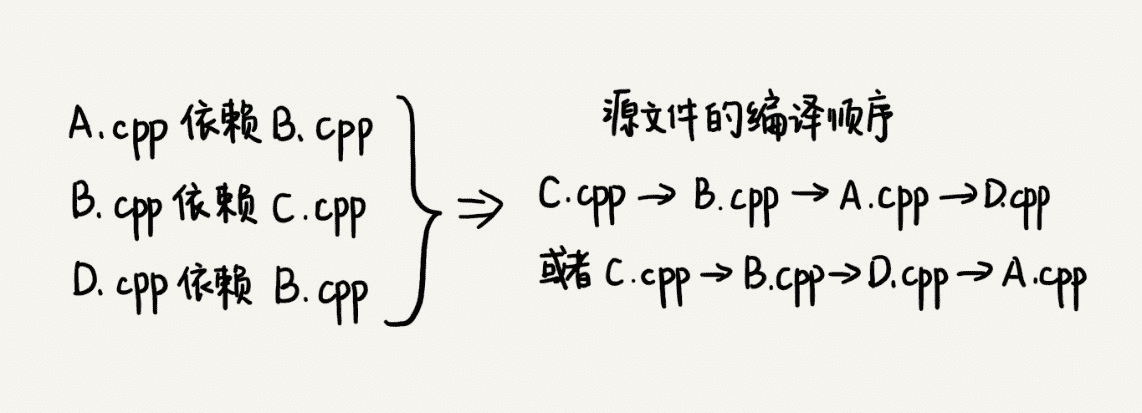
我们知道,一个完整的项目往往会包含很多代码源文件。编译器在编译整个项目的时候,需要按照依赖关系,依次编译每个源文件。比如,A.cpp 依赖 B.cpp,那在编译的时候,编译器需要先编译 B.cpp,才能编译 A.cpp。
编译器通过分析源文件或者程序员事先写好的编译配置文件(比如 Makefile 文件),来获取这种局部的依赖关系。那编译器又该如何通过源文件两两之间的局部依赖关系,确定一个全局的编译顺序呢?
算法解析
这个问题的解决思路与“图”这种数据结构的一个经典算法“拓扑排序算法”有关。那什么是拓扑排序呢?这个概念很好理解,我们先来看一个生活中的拓扑排序的例子。
我们在穿衣服的时候都有一定的顺序,我们可以把这种顺序想成,衣服与衣服之间有一定的依赖关系。比如说,你必须先穿袜子才能穿鞋,先穿内裤才能穿秋裤。假设我们现在有八件衣服要穿,它们之间的两两依赖关系我们已经很清楚了,那如何安排一个穿衣序列,能够满足所有的两两之间的依赖关系?
这就是个拓扑排序问题。从这个例子中,你应该能想到,在很多时候,拓扑排序的序列并不是唯一的。你可以看我画的这幅图,我找到了好几种满足这些局部先后关系的穿衣序列。

弄懂了这个生活中的例子,开篇的关于编译顺序的问题,你应该也有思路了。开篇问题跟这个问题的模型是一样的,也可以抽象成一个拓扑排序问题。
拓扑排序的原理非常简单,我们的重点应该放到拓扑排序的实现上面。
我前面多次讲过,算法是构建在具体的数据结构之上的。针对这个问题,我们先来看下,如何将问题背景抽象成具体的数据结构?
我们可以把源文件与源文件之间的依赖关系,抽象成一个有向图。每个源文件对应图中的一个顶点,源文件之间的依赖关系就是顶点之间的边。
如果 a 先于 b 执行,也就是说 b 依赖于 a,那么就在顶点 a 和顶点 b 之间,构建一条从 a 指向 b 的边。而且,这个图不仅要是有向图,还要是一个有向无环图,也就是不能存在像 a->b->c->a 这样的循环依赖关系。因为图中一旦出现环,拓扑排序就无法工作了。实际上,拓扑排序本身就是基于有向无环图的一个算法。
|
|
数据结构定义好了,现在,我们来看,如何在这个有向无环图上,实现拓扑排序?
拓扑排序有两种实现方法,都不难理解。它们分别是Kahn 算法和DFS 深度优先搜索算法。我们依次来看下它们都是怎么工作的。
1.Kahn 算法
Kahn 算法实际上用的是贪心算法思想,思路非常简单、好懂。
定义数据结构的时候,如果 s 需要先于 t 执行,那就添加一条 s 指向 t 的边。所以,如果某个顶点入度为 0,也就表示,没有任何顶点必须先于这个顶点执行,那么这个顶点就可以执行了。
我们先从图中,找出一个入度为 0 的顶点,将其输出到拓扑排序的结果序列中(对应代码中就是把它打印出来),并且把这个顶点从图中删除(也就是把这个顶点可达的顶点的入度都减 1)。我们循环执行上面的过程,直到所有的顶点都被输出。最后输出的序列,就是满足局部依赖关系的拓扑排序。
我把 Kahn 算法用代码实现了一下,你可以结合着文字描述一块看下。不过,你应该能发现,这段代码实现更有技巧一些,并没有真正删除顶点的操作。代码中有详细的注释,你自己来看,我就不多解释了。
|
|
2.DFS 算法
图上的深度优先搜索我们前面已经讲过了,实际上,拓扑排序也可以用深度优先搜索来实现。不过这里的名字要稍微改下,更加确切的说法应该是深度优先遍历,遍历图中的所有顶点,而非只是搜索一个顶点到另一个顶点的路径。
关于这个算法的实现原理,我先把代码贴在下面,下面给你具体解释。
|
|
这个算法包含两个关键部分。
第一部分是通过邻接表构造逆邻接表。邻接表中,边 s->t 表示 s 先于 t 执行,也就是 t 要依赖 s。在逆邻接表中,边 s->t 表示 s 依赖于 t,s 后于 t 执行。为什么这么转化呢?这个跟我们这个算法的实现思想有关。
第二部分是这个算法的核心,也就是递归处理每个顶点。对于顶点 vertex 来说,我们先输出它可达的所有顶点,也就是说,先把它依赖的所有的顶点输出了,然后再输出自己。
到这里,用 Kahn 算法和 DFS 算法求拓扑排序的原理和代码实现都讲完了。我们来看下,这两个算法的时间复杂度分别是多少呢?
从 Kahn 代码中可以看出来,每个顶点被访问了一次,每个边也都被访问了一次,所以,Kahn 算法的时间复杂度就是 O(V+E)(V 表示顶点个数,E 表示边的个数)。
DFS 算法的时间复杂度我们之前分析过。每个顶点被访问两次,每条边都被访问一次,所以时间复杂度也是 O(V+E)。
注意,这里的图可能不是连通的,有可能是有好几个不连通的子图构成,所以,E 并不一定大于 V,两者的大小关系不确定。所以,在表示时间复杂度的时候,V、E 都要考虑在内。
总结引申
在基础篇中,关于“图”,我们讲了图的定义和存储、图的广度和深度优先搜索。今天,我们又讲了一个关于图的算法,拓扑排序。
拓扑排序应用非常广泛,解决的问题的模型也非常一致。凡是需要通过局部顺序来推导全局顺序的,一般都能用拓扑排序来解决。除此之外,拓扑排序还能检测图中环的存在。对于 Kahn 算法来说,如果最后输出出来的顶点个数,少于图中顶点个数,图中还有入度不是 0 的顶点,那就说明,图中存在环。
关于图中环的检测,我们在递归那一节讲过一个例子,在查找最终推荐人的时候,可能会因为脏数据,造成存在循环推荐,比如,用户 A 推荐了用户 B,用户 B 推荐了用户 C,用户 C 又推荐了用户 A。如何避免这种脏数据导致的无限递归?这个问题,我当时留给你思考了,现在是时候解答了。
实际上,这就是环的检测问题。因为我们每次都只是查找一个用户的最终推荐人,所以,我们并不需要动用复杂的拓扑排序算法,而只需要记录已经访问过的用户 ID,当用户 ID 第二次被访问的时候,就说明存在环,也就说明存在脏数据。
|
|
如果把这个问题改一下,我们想要知道,数据库中的所有用户之间的推荐关系了,有没有存在环的情况。这个问题,就需要用到拓扑排序算法了。我们把用户之间的推荐关系,从数据库中加载到内存中,然后构建成今天讲的这种有向图数据结构,再利用拓扑排序,就可以快速检测出是否存在环了。
课后思考
- 在今天的讲解中,我们用图表示依赖关系的时候,如果 a 先于 b 执行,我们就画一条从 a 到 b 的有向边;反过来,如果 a 先于 b,我们画一条从 b 到 a 的有向边,表示 b 依赖 a,那今天讲的 Kahn 算法和 DFS 算法还能否正确工作呢?如果不能,应该如何改造一下呢?
- 我们今天讲了两种拓扑排序算法的实现思路,Kahn 算法和 DFS 深度优先搜索算法,如果换做 BFS 广度优先搜索算法,还可以实现吗?
欢迎留言和我分享,也欢迎点击“请朋友读”,把今天的内容分享给你的好友,和他一起讨论、学习。

文章作者
上次更新 2025-01-03