模型本身及其背后学习方法的泛化性能（generalization performance），也就是模型对未知数据的预测能力，是机器学习的核心问题。可在一个问题的学习中，往往会出现不同的模型在训练集上具有类似的性能，这时就需要利用模型验证来从这些备选中做出选择。

由于模型的泛化性能和它的复杂度是直接挂钩的，所以模型验证的任务就是确定模型的复杂度以避免过拟合的发生。原则上说，模型验证应该使用专门的验证数据集。可是当数据集的容量较小，不足以划分成三个部分时，验证集和测试集就可以合二为一，共同来完成对模型的选择和评价。

估计泛化性能时，最重要的依据就是模型在训练数据集上的精度（accuracy）。定性而论，模型在训练集上的精度不能太低。由于模型的拟合和评价都是在相同的训练集上完成的，因此用训练误差去估计测试误差，得到的必然是过于乐观的结果。如果在训练集上都达不到较高的精度的话，模型本身的假设就很可能存在问题（比如用线性模型来建模平方关系的数据），从而导致较大的偏差，这样的模型很难指望它在真实数据上具有良好的表现。

可另一方面，训练数据集上的正确率也不是“低低益善”，因为过低的正确率往往是欠拟合的征兆。训练数据集中的数据量一定是有限的，这些数据共同构成了高维空间上一个点集。只要模型的参数足够多，形式足够复杂，就必定可以构造出经过所有数据点的曲线或者曲面，在训练集上得到 100% 的正确率。显然，这样的模型对训练数据的拟合能力过强，不可能具备良好的泛化特性。

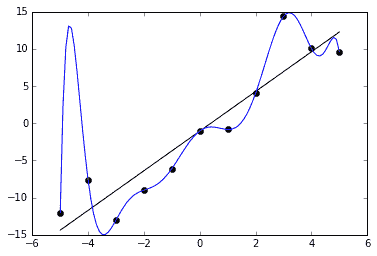
过拟合现象（图片来自维基百科）

上图就是一个典型的过拟合例子：黑点代表的离散数据可以看成是满足线性关系的原始数据和随机噪声的叠加，受噪声的影响，即使是生成数据的直线也不能完全拟合数据，总归存在一定的残留误差。如果要将残留误差降低为 0，在训练集上取得 100% 的正确率，得到的拟合结果就是龙飞凤舞的蓝色曲线。虽然这个多项式模型完美地覆盖了所有数据点，但它所代表的数据生成方式显然和黑色直线并不接近。此时，过高的训练集正确率反而与对模型优良泛化性能的追求背道而驰。

既然训练误差太高了不行，太低了也不行，那么究竟到什么程度才算合适呢？关于训练误差和泛化误差的关系，《统计学习基础》（Elements of Statistical Learning）从理论上给出了略显晦涩的解释。在这里我尝试加以解读。

分析的出发点是误差的分解理论：误差包括噪声、偏差和方差三部分。当模型的训练过程结束后，在训练集上就可以计算出模型 f^f^