不知道你是否留意过非洲的地图？和其他大洲按照地理边界划分国界的方式不同，很多非洲国家的国境线都是规则的直线条组合。这种非自然的划分背后隐藏着一段屈辱的历史：19 世纪起，欧洲的资本主义新贵们开始了对非洲的掠夺。而在巧取豪夺资源之外，他们也没有忘记抢占地盘，这些横平竖直的国境线就是对当年殖民主义者瓜分非洲无声的控诉。

下图是主要殖民国家在非洲的势力范围划分图，图片里的非洲如俎上的鱼肉般被肆意切割，切下的每一块都像黑奴一样，被烫上宗主国的烙印。

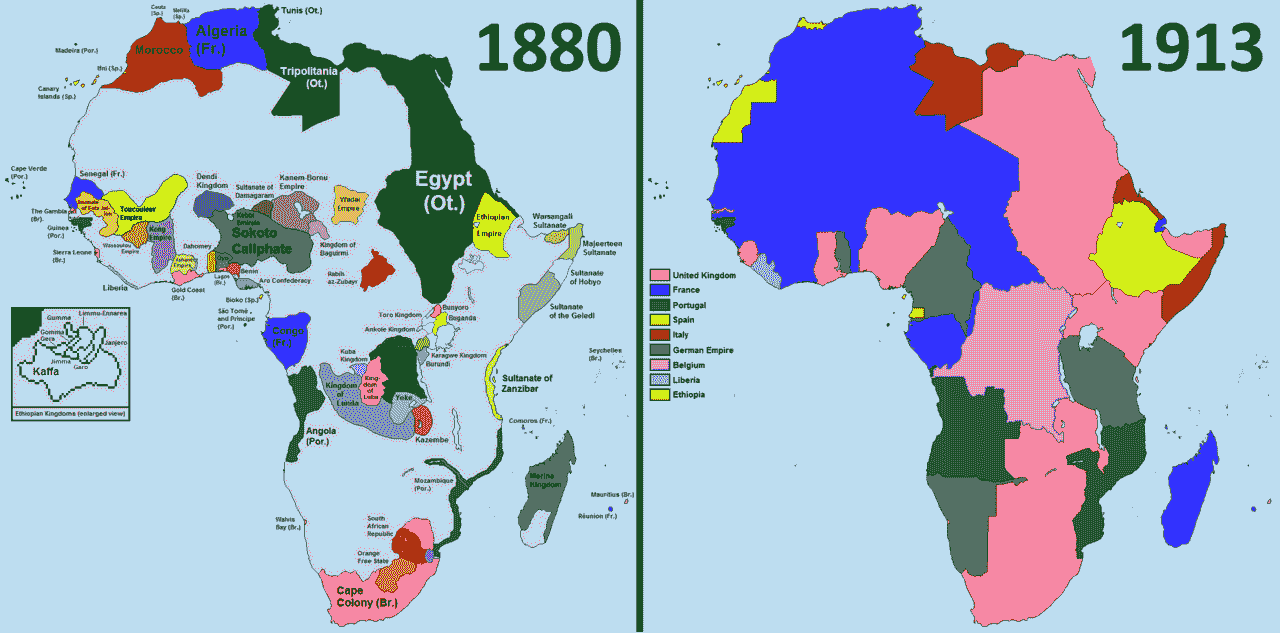
瓜分非洲（Scramble for Africa）（图片来自维基百科）

当然，我的目的不是探讨历史，举这个例子的原因是从非洲地图容易直观地联想到机器学习中基于树方法的分类结果。树模型（tree-based model）遵循“分而治之”的思路，以递推方式将特征空间划分为若干个矩形的区间，再在每个区间上拟合出一个简单的模型。在分类问题中，这个简单模型就是类别的标签选择。在“人工智能基础课”中，我曾以用于分类的决策树为例，对树模型做了介绍，你可以回忆一下。下图就是分类决策树对特征空间进行划分的一个实例。

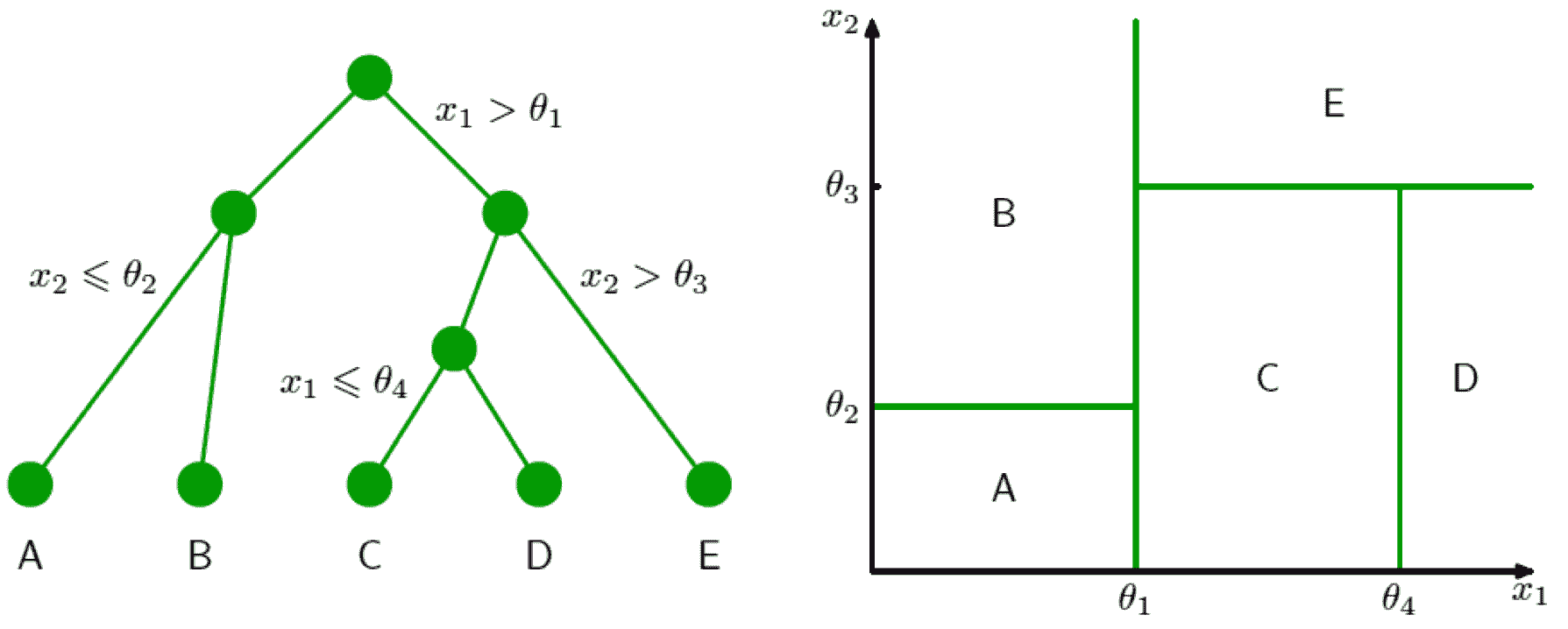
决策树的生成与对特征空间的划分（图片来自 Pattern Recognition and Machine Learning, 图 14.5 & 14.6）

这一次，我将换个角度，从线性回归模型出发来理解树模型，这种理解思路将从回归树开始。

顾名思义，回归树（regression tree）是用来完成回归任务的树模型。和全局的线性回归相比，树模型是局部化的模型，可以实现非线性的拟合。在从整体到局部的过渡中，回归树的操作和之前介绍过的回归样条方法一脉相承，采用的都是“分段函数”的思路，但两者的区别在于回归树对特征空间执行的是递归式划分（recursive partitioning）。递归的划分不要求一步到位，而是步步为营地对前一次划分的子区域继续做出细化，直到满足预先设定的要求为止。这一点在上面的图示中也有所体现。

这样看来，回归树和原始线性回归的区别仅仅在于全局和局部的差异吗？非也！回归树的表达能力强在对于特征之间相互作用（interaction）的刻画。当用来预测输出的特征有多个时，不同的特征之间很可能存在着交互作用，共同对输出产生影响，而这种影响的作用就超出了线性的范畴。假设输入的特征有 x1x1