在上一篇文章中，我和你分享了最简单的概率图模型——朴素贝叶斯分类器。由于朴素贝叶斯假定不同的属性相互独立，因而它的概率图具有发散的星型结构。但在实际当中，这样的条件独立性几乎是不可能满足的，属性之间总会有些概率性的关联，如果将属性之间的关联体现在概率图模型中，就相当于把朴素贝叶斯中互相独立的结点联结起来，得到的正是贝叶斯网络。

贝叶斯网络（Bayesian network）也叫信念网络（belief network），由一些顶点和连接某些顶点的边构成，每个顶点代表一个随机变量，带箭头的有向边则表示随机变量之间的因果关系。

从拓扑结构看，贝叶斯网络是有向无环图，“有向”指的是连接不同顶点的边是有方向的，起点和终点不能调换，这说明由因到果的逻辑关系不能颠倒；“无环”指的是从任意顶点出发都无法经过若干条边回到该点，在图中找不到任何环路，这说明任何变量都不能自己决定自己。

贝叶斯网络是对随机变量以及存在于它们之间的不确定性的一种表示（representation），它以因子分解的方式定义了联合概率分布的数据结构，还给出了这个分布中的一系列条件独立性假设。

下面这个例子出自发表于《AI 季刊》（AI Magazine）第 12 卷第 4 期的论文《傻瓜贝叶斯网络》（Bayesian networks without tears），它说明当事件之间的因果关系不能完全确定时，基于概率的贝叶斯网络是如何发挥作用的。

“假设有一天我回家晚了，还碰巧没带钥匙，所以在敲门之前我想先看看家里有没有人。我太太的习惯是不在家时把廊外灯打开，但如果有客人约定来访的话，即使她在家时也会开灯。另外，我还养了一条狗，家里没人的时候会把狗锁在院子里。但狗在院子里也不能确定地说明家里没人，因为如果狗狗犯错的话也会被不让进屋。反正不管怎样，只有狗狗在外面，听到门口有人它就会叫，但我又分辨不出到底是不是我家的狗在叫。那么问题来了，如何判断我家里到底有没有人呢？”

在这个例子中，所有的因果联系都不是绝对的，灯开不意味着家里肯定没人，狗在院子里也一样。如果灯是开着的但没有听到狗叫，或者听到狗叫但是灯没开，这些情况下就只能对家里有没有人做出概率性的推断。贝叶斯网络就是概率推断的有力工具，它的条件独立性可以在已知的概率值较少时依然做出准确的推断。下图就是利用已知的因果联系构造出的贝叶斯网络。

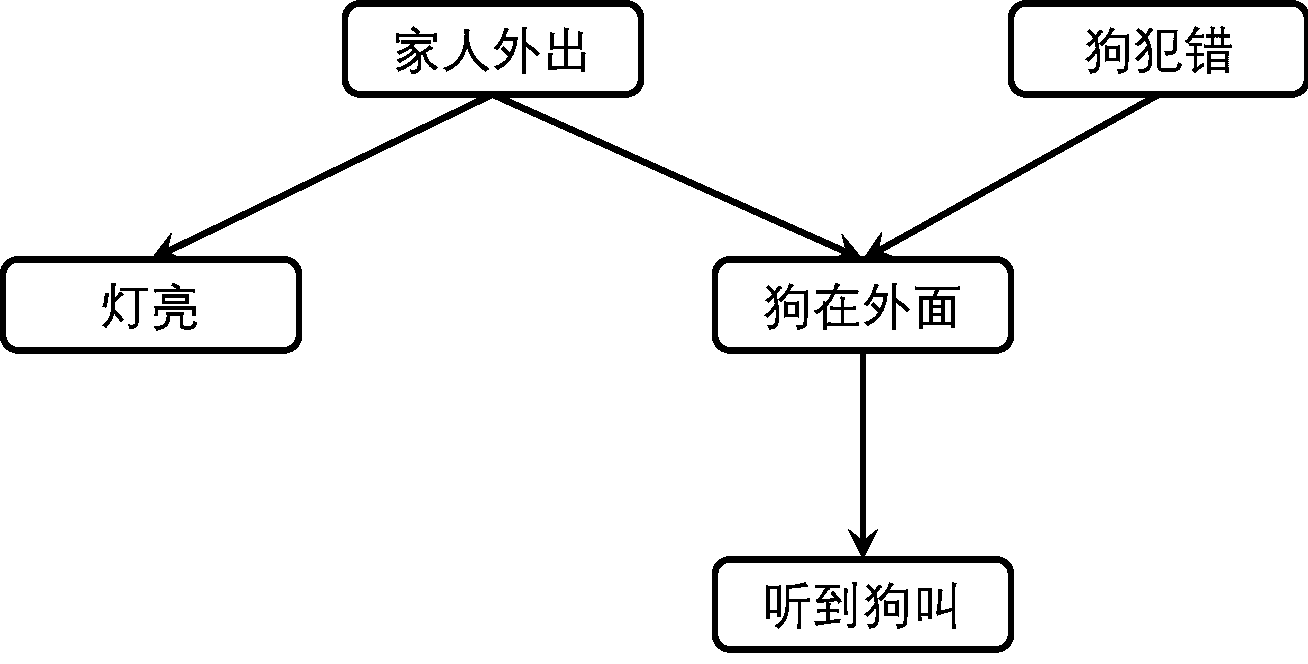
“家里有没有人”的贝叶斯网络

从结构上看，条件独立性在一定程度上简化了随机变量的关系，在给定父结点的条件下，每个结点都和它的所有非后代结点条件独立。这意味着每个结点的概率既取决于它的父结点，也取决于它的子结点。从结构上看，父结点、子结点以及子结点的后代结点共同形成一条逻辑关系上的通路，概率的变化就是在这条通路上传导。如果其他结点不在这条通路上，就大概率不会受到处在通路上的结点的影响。

在上面的例子中，“听到狗叫”是“狗在外面”的子结点，而它本身又没有后代结点。所以只要“狗在外面”这个事件确定了，那么能不能听到狗叫就不会被任何其他变量提供的信息所影响。但对于狗是不是在外面这个问题，事情就没有那么简单了，它既会受到“家人外出”和“狗犯错”这两个父结点的影响，也会受“听到狗叫”这个子结点的影响，其中每一个的变化都会改变对于“狗在外面”这个论述的判断。

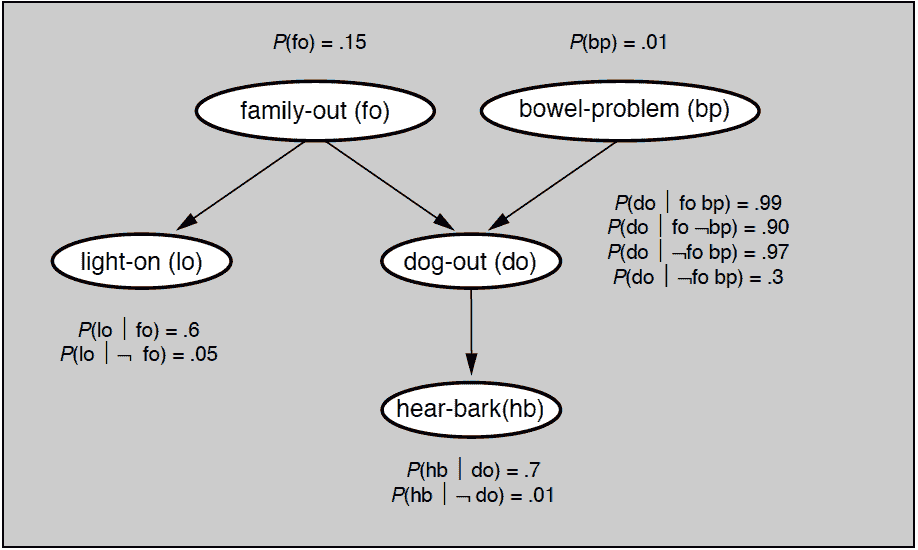
给定条件概率的贝叶斯网络

要对贝叶斯网络进行定量计算，就需要给每个根结点所表示的随机变量赋予概率值，同时给表示不同结点之间依赖关系的每条有向边所代表的所有条件概率赋值。上图给出了确定条件概率取值之后的贝叶斯网络。根据这些概率就可以计算一种情况——当灯是开着的但没有听到狗叫时，家里有人的概率。具体的求解方法今天先不讨论，留到后面再做解释，本篇先把重点放在贝叶斯网络的结构特性上。

结构上的条件独立性降低了贝叶斯网络所需要求解的概率的数目，从而在根本上降低推断的计算成本。在上面的例子中，随机变量的数目，也就是结点的数目是 5 个，每个随机变量又都只有 2 种可能的取值。在不考虑条件独立性时，要定义这 5 个随机变量的联合分布的话，就得计算 25−1=3125−1=31