在前面的几讲中，我和你分享了概率图模型中的一些代表性模型，它们都属于表示（representation）的范畴，将关系通过结点和有向边精确地表示出来。接下来，我们将对概率图模型的推断任务加以介绍。

推断（inference）是利用图结构表示的联合分布来计算某个变量的概率，得到关于目标问题的数字化结论。在概率图模型中，因子分解与条件独立性这两大法宝可以大量节约概率运算，给推断问题带来简洁高效的解法。

概率图中的推断可以分为两类：精确推断和近似推断。精确推断（exact inference）是精确计算变量的概率分布，可以在结构比较简单的模型中实现；近似推断（approximate inference）则是在不影响推理正确性的前提下，通过适当降低精度来提高计算效率，适用于结点数目多、网络结构复杂的模型。在这一讲中，我们先来分析精确推断。

精确推断最基本的方法是变量消除（variable elimination），这种方法对“与待求解的条件概率无关的变量”进行边际化处理，也就是将中间变量约掉，从而计算出目标概率。变量消除的基本思想可以通过贝叶斯网络中所举的例子来解释，问题对应的贝叶斯网络如下图所示，所有的先验概率与条件概率都在图中给出。

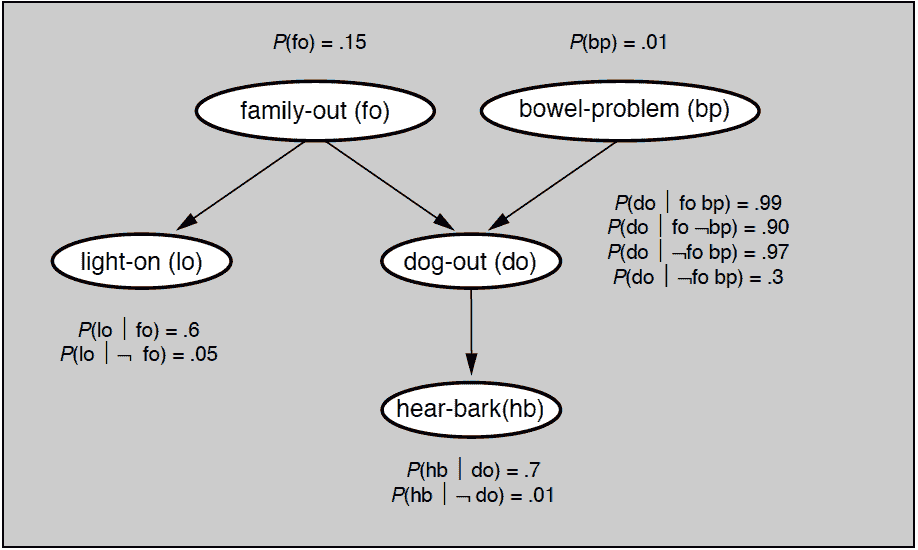
贝叶斯网络实例

如果要用变量消除法计算变量 hbhb