15_从树到图:如何让计算机学会看地图?
文章目录
你好,我是黄申。
我们经常使用手机上的地图导航 App,查找出行的路线。那计算机是如何在多个选择中找到最优解呢?换句话说,计算机是如何挑选出最佳路线的呢?
前几节,我们讲了数学中非常重要的图论中的概念,图,尤其是树中的广度优先搜索。在广度优先的策略中,因为社交网络中的关系是双向的,所以我们直接用无向边来求解图中任意两点的最短通路。
这里,我们依旧可以用图来解决这个问题,但是,影响到达最终目的地的因素有很多,比如出行的交通工具、行驶的距离、每条道路的交通状况等等,因此,我们需要赋予到达目的地的每条边不同的权重。而我们想求的最佳路线,其实就是各边权重之和最小的通路。
我们前面说了,广度优先搜索只测量通路的长度,而不考虑每条边上的权重。那么广度优先搜索就无法高效地完成这个任务了。那我们能否把它改造或者优化一下呢?
我们需要先把交通地图转为图的模型。图中的每个结点表示一个地点,每条边表示一条道路或者交通工具的路线。其中,边是有向的,表示单行道等情况。其次,边是有权重的。
假设你关心的是路上所花费的时间,那么权重就是从一点到另一点所花费的时间;如果你关心的是距离,那么权重就是两点之间的物理距离。这样,我们就把交通导航转换成图论中的一个问题:在边有权重的图中,如何让计算机查找最优通路?
基于广度优先或深度优先搜索的方法
我们以寻找耗时最短的路线为例来看看。
一旦我们把地图转换成了图的模型,就可以运用广度优先搜索,计算从某个出发点,到图中任意一个其他结点的总耗时。基本思路是,从出发点开始,广度优先遍历每个点,当遍历到某个点的时候,如果该点还没有耗时的记录,记下当前这条通路的耗时。如果该点之前已经有耗时记录了,那就比较当前这条通路的耗时是不是比之前少。如果是,那就用当前的替换掉之前的记录。
实际上,地图导航和之前社交网络最大的不同在于,每个结点被访问了一次还是多次。在之前的社交网络的案例中,使用广度优先策略时,对每个结点的首次访问就能获得最短通路,因此每个结点只需要被访问一次,这也是为什么广度优先比深度优先更有效。
而在地图导航的案例中,从出发点到某个目的地结点,可能有不同的通路,也就意味着耗时不同。而耗时是通路上每条边的权重决定的,而不是通路的长度。因此,为了获取达到某个点的最短时间,我们必须遍历所有可能的路线,来取得最小值。这也就是说,我们对某些结点的访问可能有多次。
我画了一张图,方便你理解多条通路对最终结果的影响。这张图中有 A、B、C、D、E 五个结点,分别表示不同的地点。
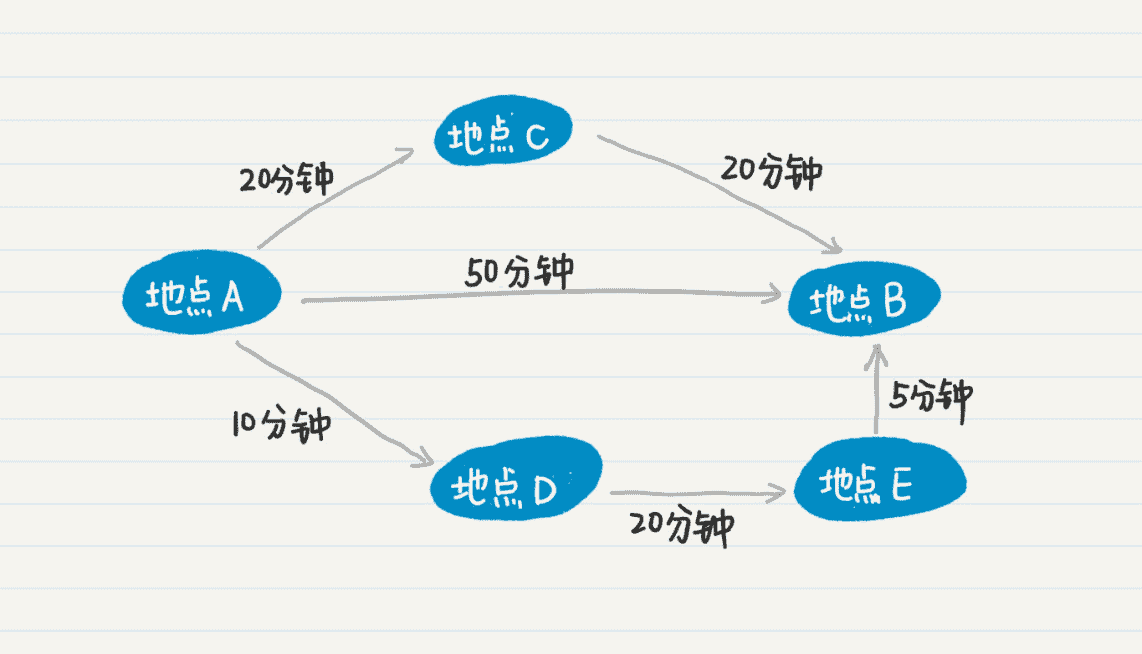
从这个图中可以看出,从 A 点出发到到目的地 B 点,一共有三条路线。如果你直接从 A 点到 B 点,度数为 1,需要 50 分钟。从 A 点到 C 点再到 B 点,虽然度数为 2,但总共只要 40 分钟。从 A 点到 D 点,到 E 点,再到最后的 B 点,虽然度数为 3,但是总耗时只有 35 分钟,比其他所有的路线更优。这种情形之下,使用广度优先找到的最短通路,不一定是最优的路线。所以,对于在地图上查找最优路线的问题,无论是广度优先还是深度优先的策略,都需要遍历所有可能的路线,然后取最优的解。
在遍历所有可能的路线时,有几个问题需要注意。
第一,由于要遍历所有可能的通路,因此一个点可能会被访问多次。当然,这个“多次“是指某个结点出现在不同通路中,而不是多次出现在同一条通路中。因为我们不想让用户总是兜圈子,所以需要避免回路。
第二,如果某个结点 x 和起始点 s 之间存在多个通路,每当 x 到 s 之间的最优路线被更新之后,我们还需要更新所有和 x 相邻的结点之最优路线,计算复杂度会很高。
一个优化的版本:Dijkstra 算法
无论是广度优先还是深度优先的实现,算法对每个结点的访问都可能多于一次。而访问多次,就意味着要消耗更多的计算机资源。那么,有没有可能在保证最终结果是正确的情况下,尽可能地减少访问结点的次数,来提升算法的效率呢?
首先,我们思考一下,对于某些结点,是不是可以提前获得到达它们的最终的解(例如最短耗时、最短距离、最低价格等等),从而把它们提前移出遍历的清单?如果有,是哪些结点呢?什么时候可以把它们移出呢?Dijkstra 算法要登场了!它简直就是为了解决这些问题量身定制的。
Dijkstra 算法的核心思想是,对于某个结点,如果我们已经发现了最优的通路,那么就无需在将来的步骤中,再次考虑这个结点。Dijkstra 算法很巧妙地找到这种点,而且能确保已经为它找到了最优路径。
1.Dijkstra 算法的主要步骤
让我们先来看看 Dijkstra 算法的主要步骤,然后再来理解,它究竟是如何确定哪些结点已经拥有了最优解。
首先你需要了解几个符号。
第一个是 source,我们用它表示图中的起始点,缩写是 s。
然后是 weight,表示二维数组,保存了任意边的权重,缩写为 w。w[m, n] 表示从结点 m 到结点 n 的有向边之权重,大于等于 0。如果 m 到 n 有多条边,而且权重各自不同,那么取权重最小的那条边。
接下来是 min_weight,表示一维数组,保存了从 s 到任意结点的最小权重,缩写为 mw。假设从 s 到某个结点 m 有多条通路,而每条通路的权重是这条通路上所有边的权重之和,那么 mw[m] 就表示这些通路权重中的最小值。mw[s]=0,表示起始点到自己的最小权重为 0。
最后是 Finish,表示已经找到最小权重的结点之集合,缩写为 F。一旦结点被放入集合 F,这个结点就不再参与将来的计算。
初始的时候,Dijkstra 算法会做三件事情。第一,把起始点 s 的最小权重赋为 0,也就是 mw[s] = 0。第二,往集合 F 里添加结点 s,F 包含且仅包含 s。第三,假设结点 s 能直接到达的边集合为 M,对于其中的每一条边 m,则把 mw[m] 设为 w[s, m],同时对于所有其他 s 不能直接到达的结点,将通路的权重设为无穷大。
然后,Dijkstra 算法会重复下列两个步骤。
第一步,查找最小 mw。从 mw 数组选择最小值,则这个值就是起始点 s 到所对应的结点的最小权重,并且把这个点加入到 F 中,针对这个点的计算就算完成了。比如,当前 mw 中最小的值是 mw[x]=10,那么结点 s 到结点 x 的最小权重就是 10,并且把结点 x 放入集合 F,将来没有必要再考虑点 x,mw[x] 可能的最小值也就确定为 10 了。
第二步,更新权重。然后,我们看看,新加入 F 的结点 x,是不是可以直接到达其他结点。如果是,看看通过 x 到达其他点的通路权重,是否比这些点当前的 mw 更小,如果是,那么就替换这些点在 mw 中的值。例如,x 可以直接到达 y,那么把 (mw[x] + w[x, y]) 和 mw[y] 比较,如果 (mw[x] + w[x, y]) 的值更小,那么把 mw[y] 更新为这个更小的值,而我们把 x 称为 y 的前驱结点。
然后,重复上述两步,再次从 mw 中找出最小值,此时要求 mw 对应的结点不属于 F,重复上述动作,直到集合 F 包含了图的所有结点,也就是说,没有结点需要处理了。
字面描述有些抽象,我用一个具体的例子来解释一下。你可以看我画的这个图。
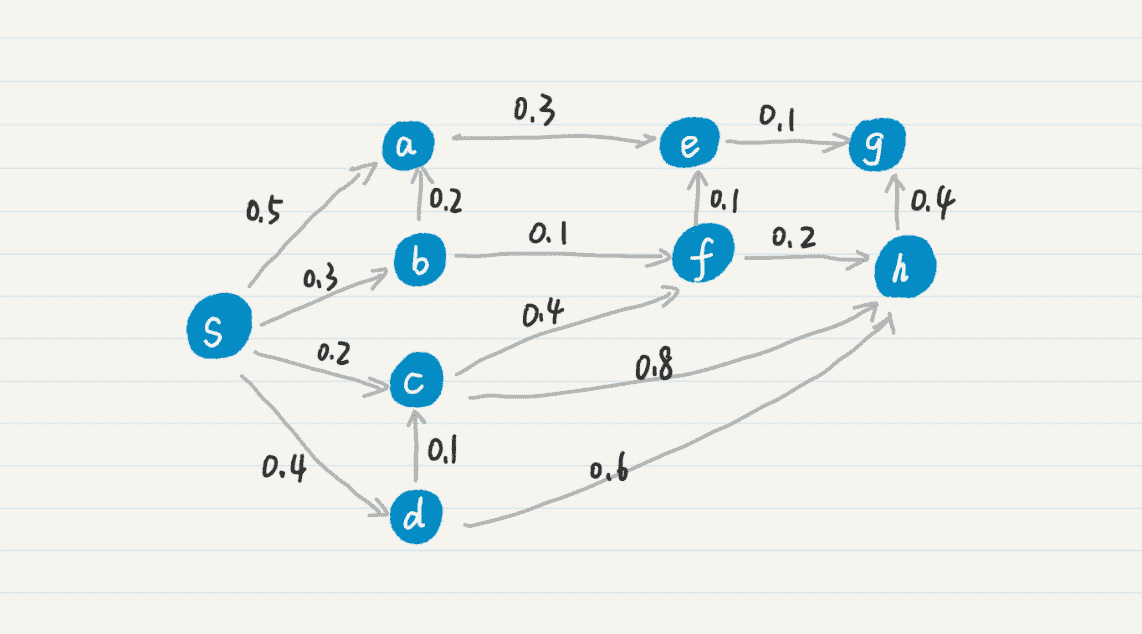
我们把结点 s 放入集合 F。同 s 直接相连的结点有 a、b、c 和 d,我把它们的 mw 更新为 w 数组中的值,就可以得到如下结果:

然后,我们从 mw 选出最小的值 0.2,把对应的结点 c 加入集合 F,并更新和 c 直接相连的结点 f、h 的 mw 值,得到如下结果:
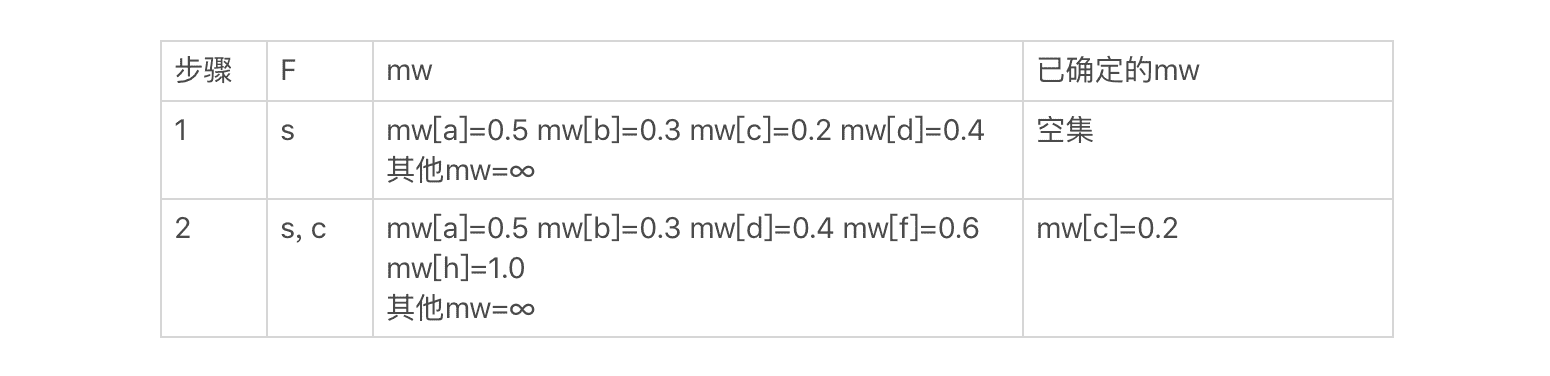
然后,我们从 mw 选出最小的值 0.3,把对应的结点 b 加入集合 F,并更新和 b 直接相连的结点 a 和 f 的 mw 值。以此逐步类推,可以得到如下的最终结果:

你可以试着自己从头到尾推导一下,看看结果是不是和我的一致。
说到这里,你可能会产生一个疑问:Dijkstra 算法提前把一些结点排除在计算之外,而且没有遍历全部可能的路径,那么它是如何确保找到最优路径的呢?下面,我们就来看看这个问题的答案。Dijkstra 算法的步骤看上去有点复杂,不过其中最关键的两步是:第一个是每次选择最小的 mw;第二个是,假设被选中的最小 mw,所对应的结点是 x,那么查看和 x 直接相连的结点,并更新它们的 mw。
2. 为什么每次都要选择最小的 mw?
最小的、非无穷大的 mw 值,对应的结点是还没有加入 F 集合的、且和 s 有通路的那些结点。假设当前 mw 数组中最小的值是 mw[x],对应的结点是 x。如果边的权重都是正值,那么通路上的权重之和是单调递增的,所以其他通路的权重之和一定大于当前的 mw[x],因此即使存在其他的通路,其权重也会比 mw[x] 大。
你可以结合这个图,来理解我刚才这段话。
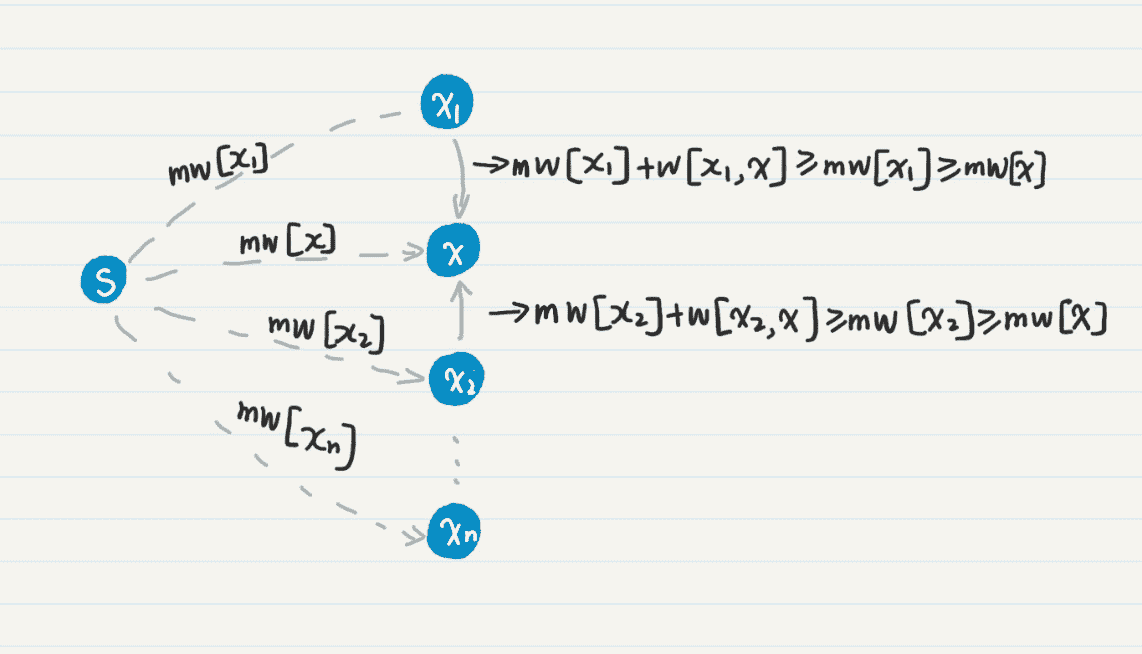
图中的虚线表示省去了通路中间的若干结点。mw[x] 是当前 mw 数组中的最小值,所以它小于等于任何一个 mw[xn],其中 xn 不等于 x。
我们假设存在另一个通路,通过 xnxn
文章作者
上次更新 2025-01-03