16_时间和空间复杂度(上):优化性能是否只是“纸上谈兵”?
文章目录
你好,我是黄申。
作为程序员,你一定非常清楚复杂度分析对编码的重要性。计算机系统从最初的设计、开发到最终的部署,要经过很多的步骤,而影响系统性能的因素有很多。我把这些因素分为三大类:算法理论上的计算复杂度、开发实现的方案和硬件设备的规格。
如果将整个系统的构建比作生产汽车,那么计算复杂度相当于在蓝图设计阶段,对整个汽车的性能进行评估。如果我们能够进行准确的复杂度分析,那么就能从理论上预估汽车的各项指标,避免生产出一辆既耗油又开得很慢的汽车。
可是,你也常常会发现,要准确地分析复杂度并不容易。这一讲,我来说说如何使用数学的思维,来进行系统性的复杂度分析。
基本概念
我先带你简短回顾一下几个重要概念,便于你稍后更好地理解本节的内容。
算法复杂度是一个比较抽象的概念,通常只是一个估计值,它用于衡量程序在运行时所需要的资源,用于比较不同算法的性能好坏。同一段代码处理不同的输入数据所消耗的资源也可能不同,所以分析复杂度时,需要考虑三种情况,最差情况、最好情况和平均情况。
复杂度分析会考虑性能的各个方面,不过我们最关注的是两个部分,时间和空间。时间因素是指程序执行的耗时多少,空间因素是程序占用内存或磁盘存储的多少。因此,我们把复杂度进一步细分为时间复杂度和空间复杂度。
我们通常所说的时间复杂度是指渐进时间复杂度,表示程序运行时间随着问题复杂度增加而变化的规律。同理,空间复杂度是指渐进空间复杂度,表示程序所需要的存储空间随着问题复杂度增加而变化的规律。我们可以使用大 O 来表示这两者。
我这里不会讲太多的基本概念,而是通过数学的思维,总结一些比较通用的方法和规则,帮助你快速、准确地进行复杂度分析。
6 个通用法则
复杂度分析有时看上去很难,其实呢,我们只要通过一定的方法进行系统性的分析,就能得找正确的结论。我通过自身的一些经验,总结了 6 个法则,相信它们对你会很有帮助。
1. 四则运算法则
对于时间复杂度,代码的添加,意味着计算机操作的增加,也就是时间复杂度的增加。如果代码是平行增加的,就是加法。如果是循环、嵌套或者函数的嵌套,那么就是乘法。
比如二分查找的代码中,第一步是对长度为 n 的数组排序,第二步是在这个已排序的数组中进行查找。这两个部分是平行的,所以计算时间复杂度时可以使用加法。第一步的时间复杂度是 O(nlogn),第二步的时间复杂度是 O(logn),所以时间复杂度是 O(nlogn)+O(logn)。
你还记得在第 3 讲我讲的查字典的例子吗?
|
|
这里面的 Arrays.sort(dictionary),我用了 Java 自带的排序函数,时间复杂度为 O(nlogn),而 Lesson3_3.search 是我自己实现的二分查找,时间复杂度为 O(logn)。两者是并行的,并依次执行,因此总的时间复杂度是两者相加。
我们再来看另外一个例子。从 n 个元素中选出 3 个元素的可重复排列,使用 3 层循环的嵌套,或者是 3 层递归嵌套,这里时间复杂度计算使用乘法。由于 n*n*n=n3,时间复杂度是 O(n3)。对应加法和乘法,分别是减法和除法。如果去掉平行的代码,就减掉相应的时间复杂度。如果去掉嵌套内的循环或函数,就除去相应的时间复杂度。
对于空间复杂度,同样如此。需要注意的是,空间复杂度看的是对内存空间的使用,而不是计算的次数。如果语句中没有新开辟空间,那么无论是平行增加还是嵌套增加代码,都不会增加空间复杂度。
2. 主次分明法则
这个法则主要是运用了数量级和运算法则优先级的概念。在刚刚介绍的第一个法则中,我们会对代码不同部分所产生的复杂度进行相加或相乘。使用加法或减法时,你可能会遇到不同数量级的复杂度。这个时候,我们只需要看最高数量级的,而忽略掉常量、系数和较低数量级的复杂度。
在介绍第一个法则的时候,我说了先排序、后二分查找的总时间复杂度是 O(nlogn) + O(logn)。实际上,我贴出的代码中还有数组初始化、变量赋值、Console 输出等步骤,如果细究的话,时间复杂度应该是 O(nlogn) + O(logn) + O(3),但是和 O(nlogn) 相比,常量和 O(logn) 这种数量级都是可以忽略的,所以最终简化为 O(nlogn)。
再举个例子,我们首先通过随机函数生成一个长度为 n 的数组,然后生成这个数组的全排列。通过循环,生成 n 个随机数的时间复杂度为 O(n),而全排列的时间复杂度为 O(n!),如果使用四则运算法则,总的时间复杂为 O(n)+O(n!)。
不过,由于 n! 的数量级远远大于 n,所以我们可以把总时间复杂度简化为 O(n!)。这对于空间复杂度同样适用。假设我们计算一个长度为 n 的向量和一个维度为 [n*n] 的矩阵之乘积,那么总的空间复杂度可以由 (O(n)+O(n2)) 简化为 O(n2)。
注意,这个法则对于乘法或除法并不适用,因为乘法或除法会改变参与运算的复杂度的数量级。
3. 齐头并进法则
这个法则主要是运用了多元变量的概念,其核心思想是复杂度可能受到多个因素的影响。在这种情况下,我们要同时考虑所有因素,并在复杂度公式中体现出来。
我在之前的文章中,介绍了使用动态规划解决的编辑距离问题。从解决方案的推导和代码可以看出,这个问题涉及两个因素:参与比较的第一个字符串的长度 n 和第二个字符串的长度 m。代码使用了两次嵌套循环,第一层循环的长度是 n,第二层循环的长度为 m,根据乘法法则,时间复杂度为 O(n*m)。而空间复杂度,很容易从推导结果的状态转移表得出,也是 O(n*m)。
4. 排列组合法则
排列组合的思想不仅出现在数学模型的设计中,同样也会出现在复杂度分析中,它经常会用在最好、最坏和平均复杂度分析中。
我们来看个简单的算法题。
给定两个不同的字符 a 和 b,以及一个长度为 n 的字符数组。字符数组里的字符都只出现过一次,而且一定存在一个 a 和一个 b,请输出 a 和 b 之间的所有字符,包括 a 和 b。假设我们的算法是按照数组下标从低到高的顺序依次扫描数组,那么时间复杂度是多少呢?这里时间复杂度是由被扫描的数组元素之数量决定的,但是要准确的求解并不容易。仔细思考一下,你会发现被扫描的元素之数量存在很多可能的值。
首先,考虑字母出现的顺序,第一个遇到的字母有 2 个选择,a 或者 b。而第二个字母只有 1 个选择,这就是 2 个元素的全排列。下面我们把两种情况分开来看.
第一种情况是 a 在 b 之前出现。接下来是 a 和 b 之间的距离,这会决定我们要扫描多少个字符。两者之间的距离最大为 n-1,最小为 1,所以最坏的时间复杂度为 O(n-1),根据主次分明法则,简化为 O(n),最好复杂度为 O(1)。
平均复杂度的计算稍微繁琐一些。如果距离为 n-1,只有 1 种可能,a 为数组中第一个字符,b 为数组中最后一个字符。如果距离为 n-2,那么 a 字符的位置有 2 种可能,b 在 a 位置确定的情况下只有 1 种可能,因此排列数是 2。以此类推,如果距离为 n-3,那么有 3 种可能,一直到距离 1,有 n-1 种可能。所以平均的扫描次数为 (1 *(n-1) + 2 *(n-2) + 3 (n -3) + … + (n-1) 1) / (1 + 2 + … + n),最后时间复杂度简化为 O(n)。
第二种情况是 b 在 a 之前出现。这个分析过程和第一种情况类似。我们假设第一种和第二种情况出现的几率相等,那么综合两种情况,可以得出平均复杂度为 O(n)。
5. 一图千言法则
在之前的文章中,我提到了很多数学和算法思想都体现了树这种结构,通过画图它们内在的联系就一目了然了。同样,这些树结构也可以帮助我们分析某些算法的复杂度。
就以我们之前介绍的归并排序为例。这个算法分为数据的切分和归并两大阶段,每个阶段的数据划分不同,分组数量也不同,感觉上时间复杂度不太好计算。下面我们来看一个例子,帮助你理解。
假设等待排序的数组长为 n。首先,看数据切分阶段。数据切分的次数,就是切分阶段那棵树的非叶子结点之数量。这个切分阶段的树是一棵满二叉树,叶子结点是 n 个,那么非叶子结点的数量就是 n-1 个,所以切分的次数也就是 n-1 次。如果我们切分数据的时候,并不重新生成新的数据,而只是生成切分边界的下标,那么时间复杂度就是 O(n-1)。

在数据归并阶段,我们看二叉树的高度,为 log2n,因此归并的次数为 log2n。另外,无论数组被细分成多少个小的部分,每次归并都需要扫描整个长度为 n 的数组,因此归并阶段的时间复杂度为 nlog2n。

两个阶段加起来的时间复杂度为 O(n-1)+nlog2n,最终简化为 nlogn。是不是很直观?
我再放出我们之前讲二分查找所用的图,你可以结合这个例子进一步理解。

当然,除了图论,很多简单的图表也能帮助到我们的分析。
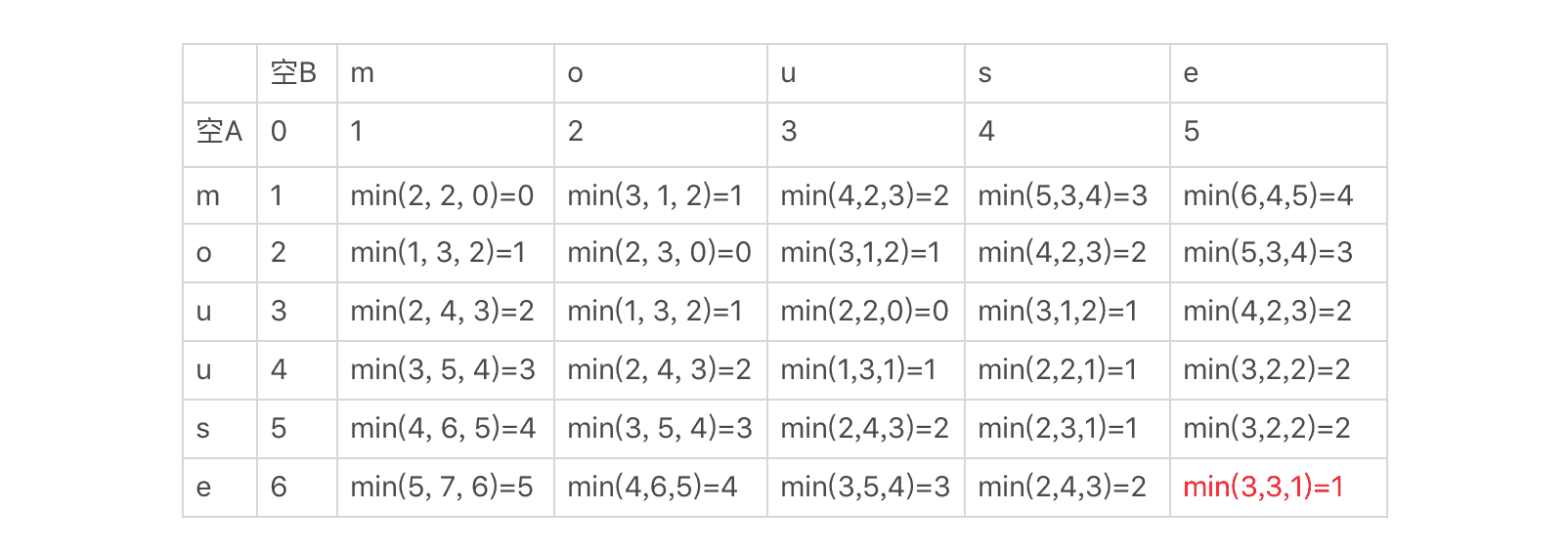
例如,在使用动态规划法的时候,我们经常要画出状态转移的表格。看到这类表格,我们可以很容易地得出该算法的时间复杂度和空间复杂度。以编辑距离为例,参看下面这个示例的图表,我们可以发现每个单元格都对应了 3 次计算,以及一个存储单元,而总共的单元格数量为 m*n,m 为第一个字符串的长度,n 为第二个字符串的长度。所以,我们很快就能得出这种算法的时间复杂度为 O(3m*n),简写为 O(m*n),空间复杂度为 O(m*n)。
6. 时空互换法则
在给定的计算量下,通常时间复杂度和空间复杂度呈现数学中的反比关系。这就说明,如果我们没法降低整体的计算量,那么也许可以通过增加空间复杂度来达到降低时间复杂度的目的,或者反之,通过增加时间复杂度来降低空间复杂度。
对于这个规则最直观的例子就是缓存系统。在没有缓存系统的时候,每次请求都要服务器来处理,因此时间复杂度比较高。如果使用了缓存系统,那么我们会消耗更多的内存空间,但是降低了请求相应的时间。
说到这,你也许会问,在使用广度优先策略优化聚合操作的时候,无论是时间还是空间复杂度,都大幅降低了啊?请注意,这里时空互换法则有个前提条件,就是计算量固定。而聚合操作的优化,是利用了广度优先的特点,大幅减少了整体的计算量,因此可以保证时间和空间复杂度都得到降低。
小结
时间复杂度和空间复杂度的概念,你一定不陌生。可是,在实际运用中,你可能就会发现复杂度分析并不是那么简单。这一节我通过个人的一些经验,从数学思维的角度出发,总结了几条常用的法则,对你会有所帮助。
这些总结可能还是过于抽象,下一讲中,我会通过几个案例分析,来讲讲如何使用这些法则。

思考题
请尝试使用本次介绍的规则,分析一下双向广度优先搜索的时间和空间复杂度。
欢迎在留言区交作业,并写下你今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。

文章作者
上次更新 2025-01-03