18_移进和规约:用LR算法推演一个实例
文章目录
到目前为止,我们所讨论的语法分析算法,都是自顶向下的。与之相对应的,是自底向上的算法,比如本节课要探讨的 LR 算法家族。
LR 算法是一种自底向上的算法,它能够支持更多的语法,而且没有左递归的问题。第一个字母 L,与 LL 算法的第一个 L 一样,代表从左向右读入程序。第二个字母 R,指的是 RightMost(最右推导),也就是在使用产生式的时候,是从右往左依次展开非终结符。例如,对于“add->add+mul”这样一个产生式,是优先把 mul 展开,然后再是 add。在接下来的讲解过程中,你会看到这个过程。
自顶向下的算法,是递归地做模式匹配,从而逐步地构造出 AST。那么自底向上的算法是如何构造出 AST 的呢?答案是用移进 - 规约的算法。
本节课,我就带你通过移进 - 规约方法,自底向上地构造 AST,完成语法的解析。接下来,我们先通过一个例子看看自底向上语法分析的过程。
通过实例了解自底向上语法分析的过程
我们选择熟悉的语法规则:
|
|
然后来解析“2+3*5”这个表达式,AST 如下:
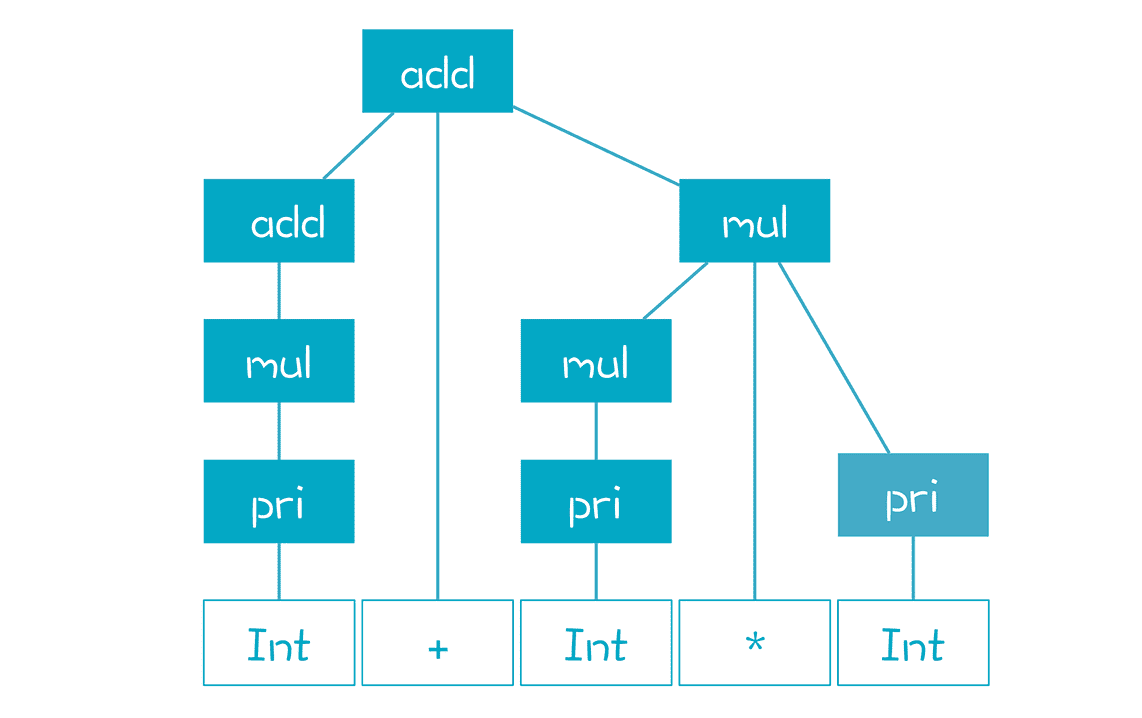
我们分步骤看一下解析的具体过程。
第 1 步,看到第一个 Token,是 Int,2。我们把它作为 AST 的第一个节点,同时把它放到一个栈里(就是图中红线左边的部分)。这个栈代表着正在处理的一些 AST 节点,把 Token 移到栈里的动作叫做移进(Shift)。

第 2 步,根据语法规则,Int 是从 pri 推导出来的(pri->Int),那么它的上级 AST 肯定是 pri,所以,我们给它加了一个父节点 pri,同时,也把栈里的 Int 替换成了 pri。这个过程是语法推导的逆过程,叫做规约(Reduce)。
Reduce 这个词你在学 Map-Reduce 时可能接触过,它相当于我们口语化的“倒推”。具体来讲,它是从工作区里倒着取出 1 到 n 个元素,根据某个产生式,组合出上一级的非终结符,也就是 AST 的上级节点,然后再放进工作区(也就是竖线的左边)。
这个时候,栈里可能有非终结符,也可能有终结符,它仿佛是我们组装 AST 的一个工作区。竖线的右边全都是 Token(也就是终结符),它们在等待处理。
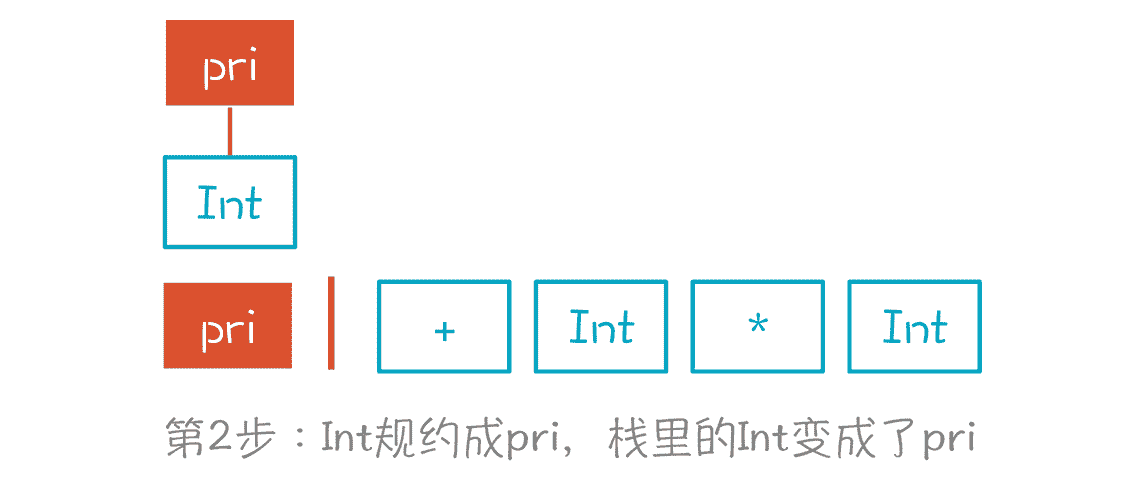
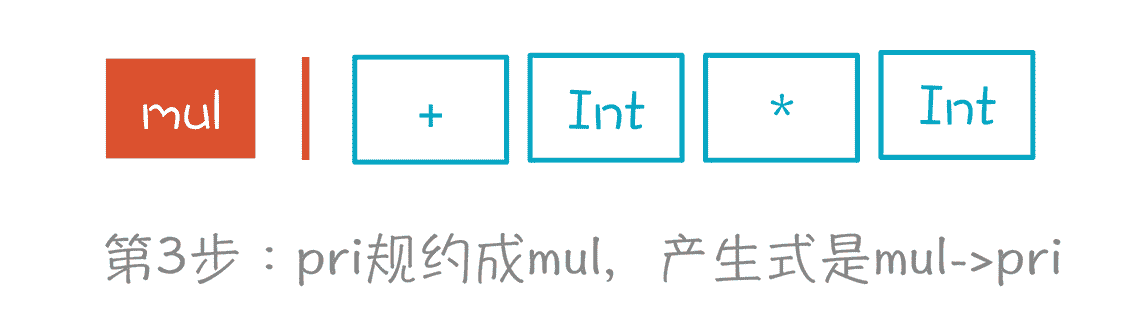
第 3 步,与第 2 步一样,因为 pri 只能是 mul 推导出来的,产生式是“mul->pri”,所以我们又做了一次规约。
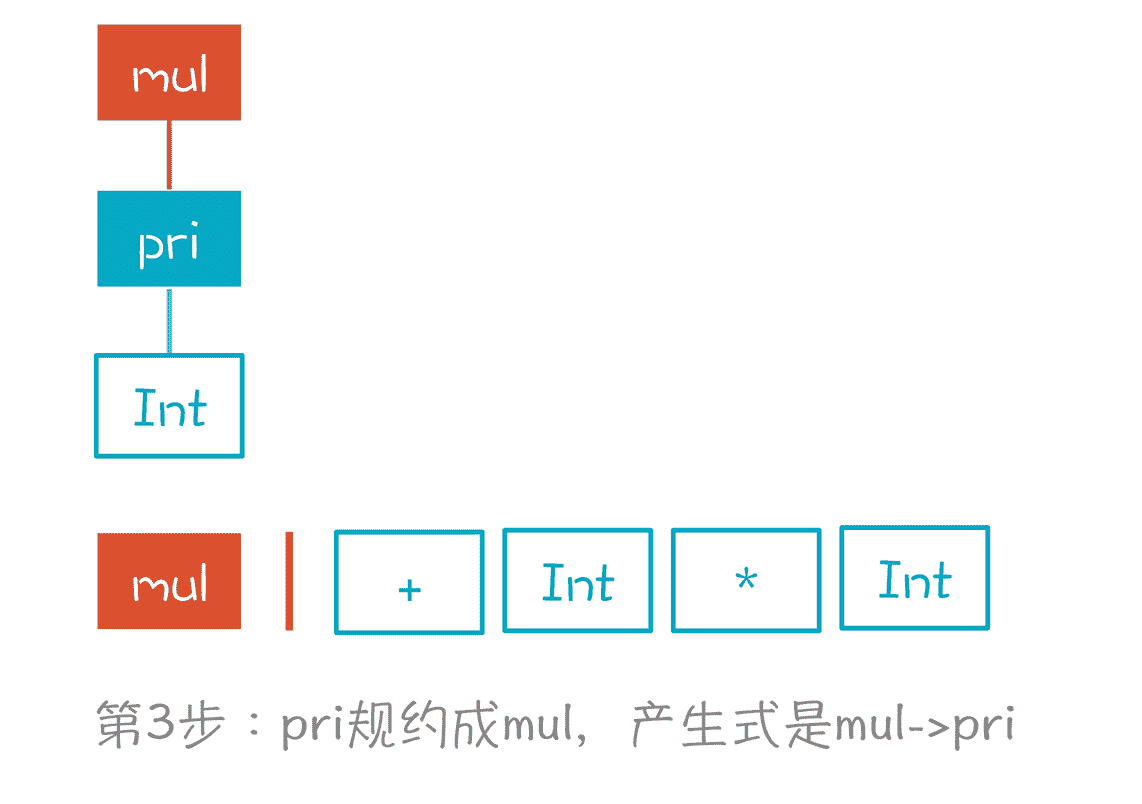
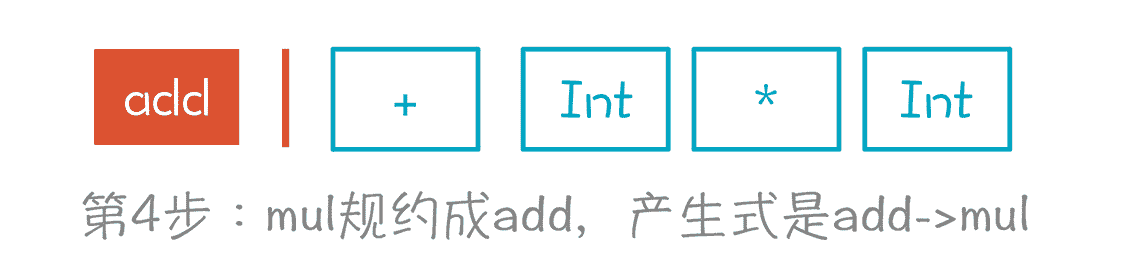
第 4 步,我们根据“add->mul”产生式,将 mul 规约成 add。至此,我们对第一个 Token 做了 3 次规约,已经到头了。这里为什么做规约,而不是停在 mul 上,移进 + 号,是有原因的。因为没有一个产生式,是 mul 后面跟 + 号,而 add 后面却可以跟 + 号。
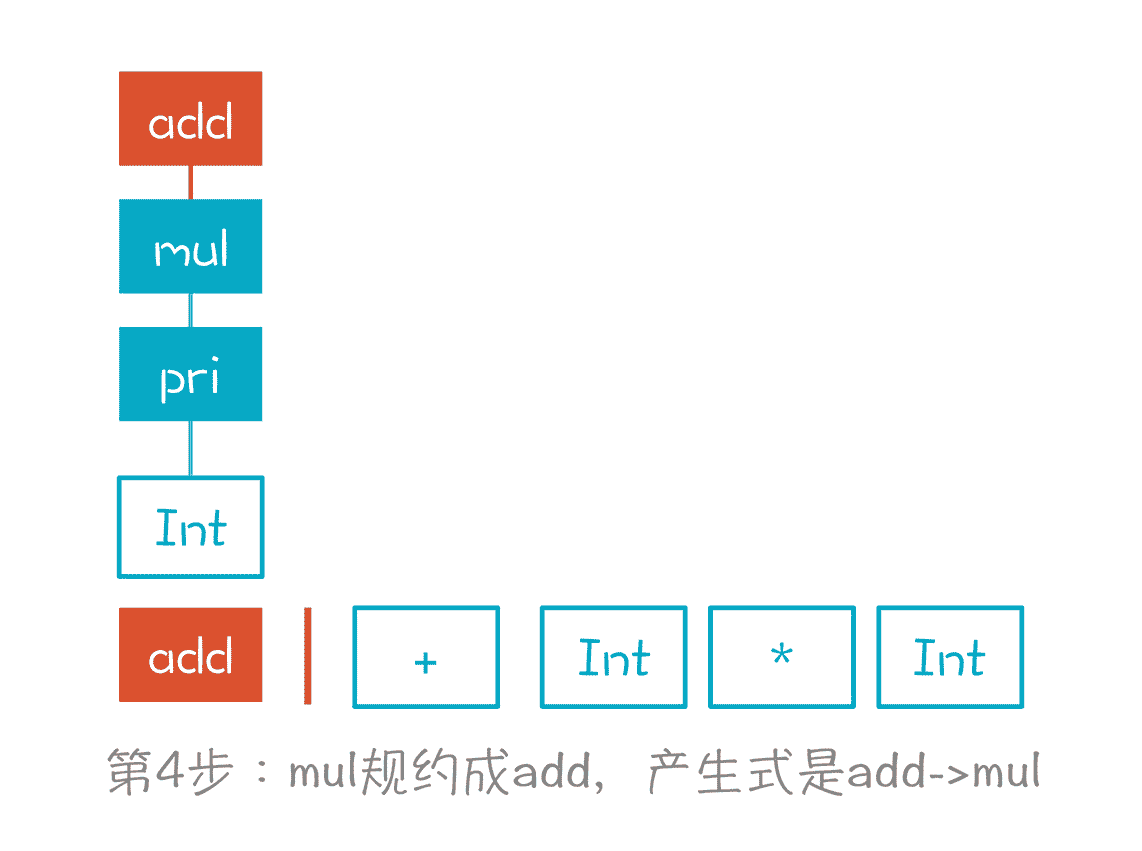
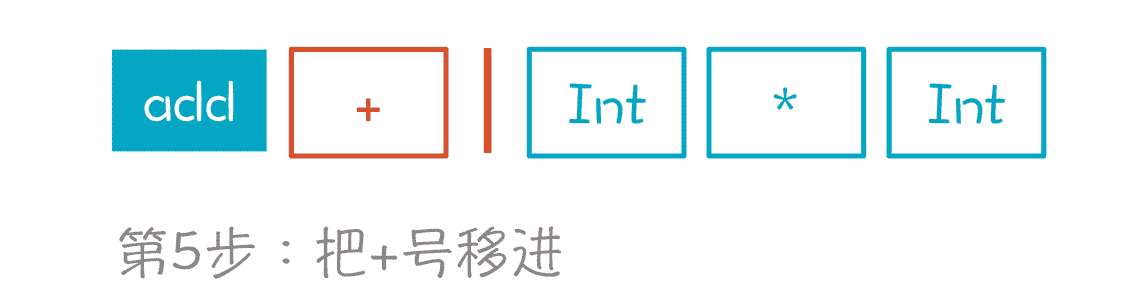
第 5 步,移进 + 号。现在栈里有两个元素了,分别是 add 和 +。
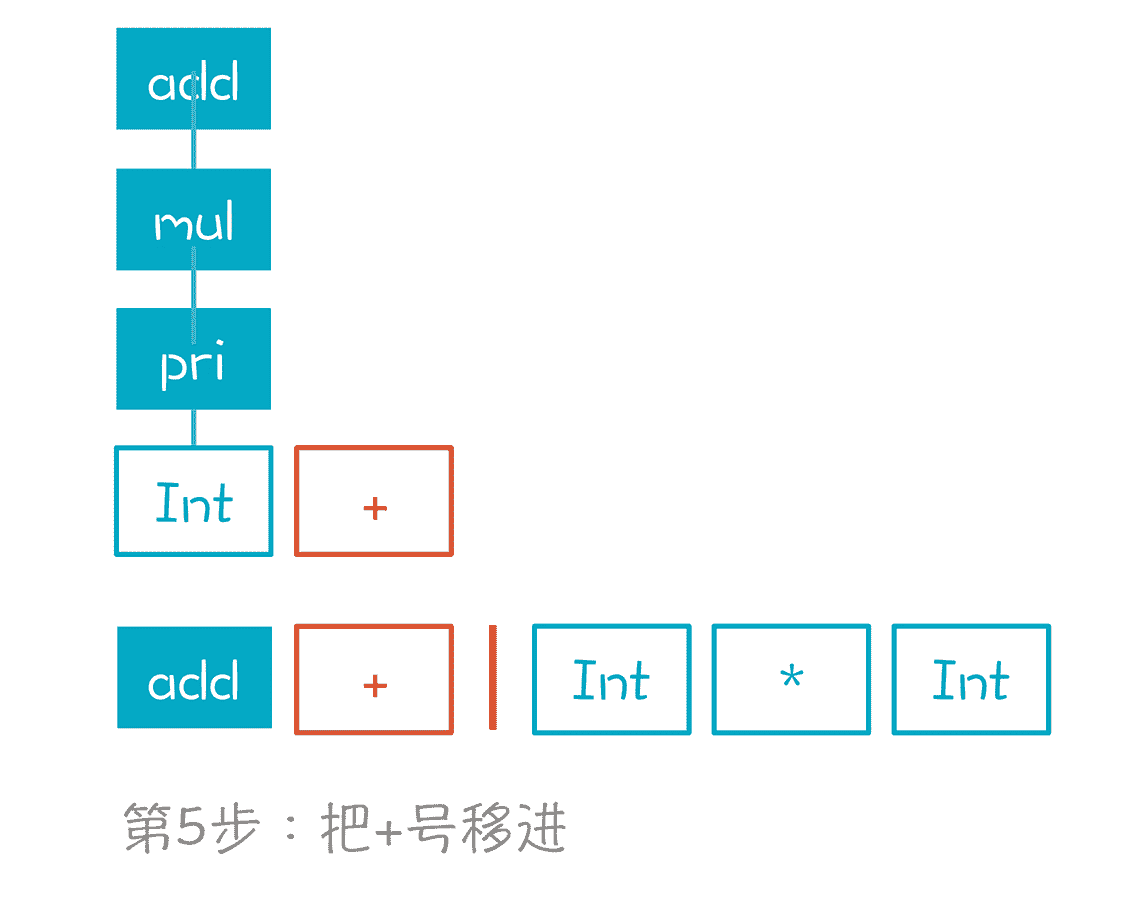
第 6 步,移进 Int,也就是数字 3。栈里现在有 3 个元素。
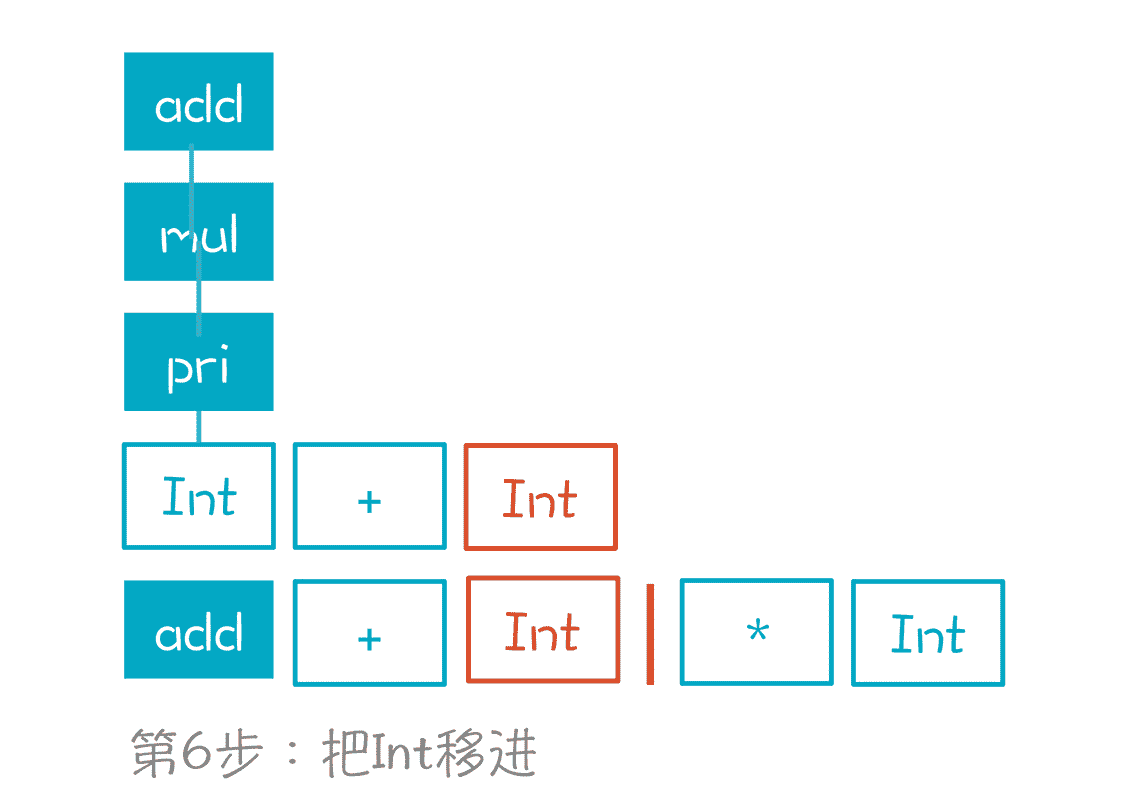
第 7 到第 8 步,Int 规约到 pri,再规约到 mul。
到目前为止,我们做规约的方式都比较简单,就是对着栈顶的元素,把它反向推导回去。
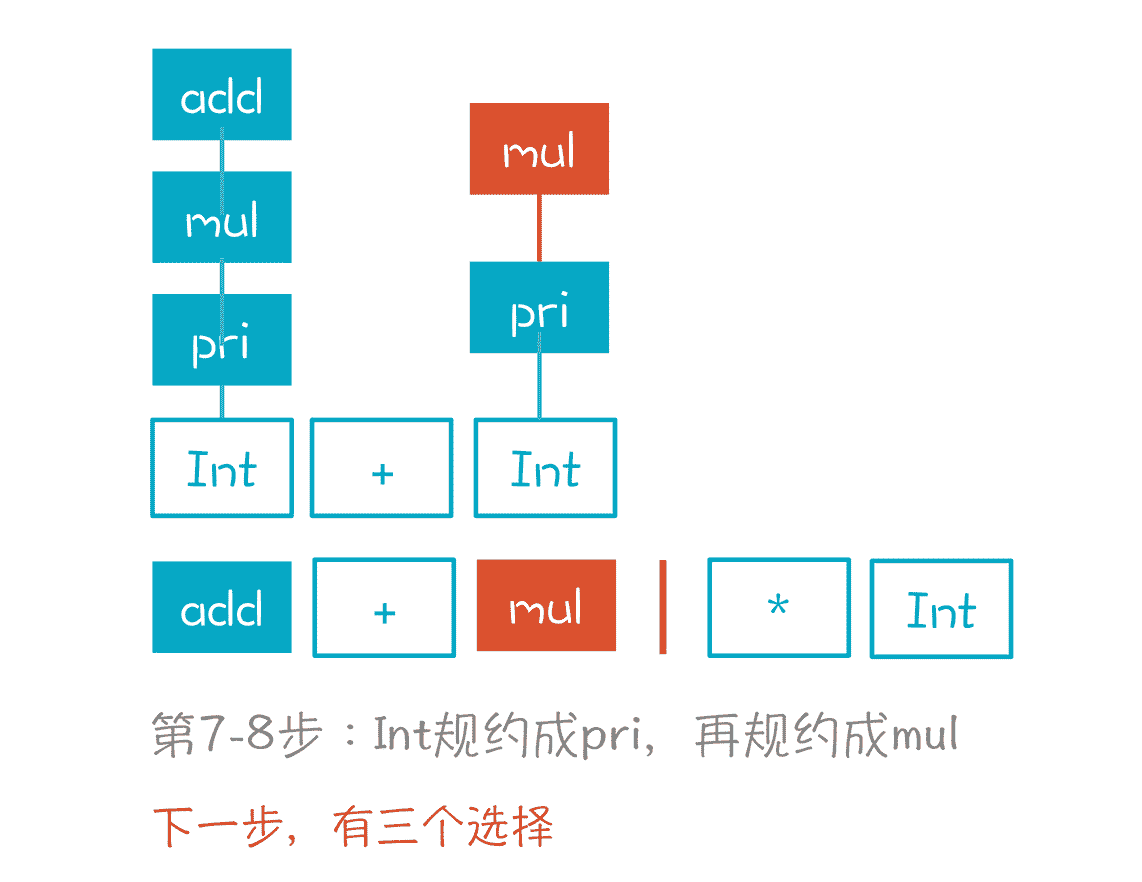
第 9 步,我们面临 3 个选择,比较难。
第一个选择是继续把 mul 规约成 add,第二个选择是把“add+mul”规约成 add。这两个选择都是错误的,因为它们最终无法形成正确的 AST。
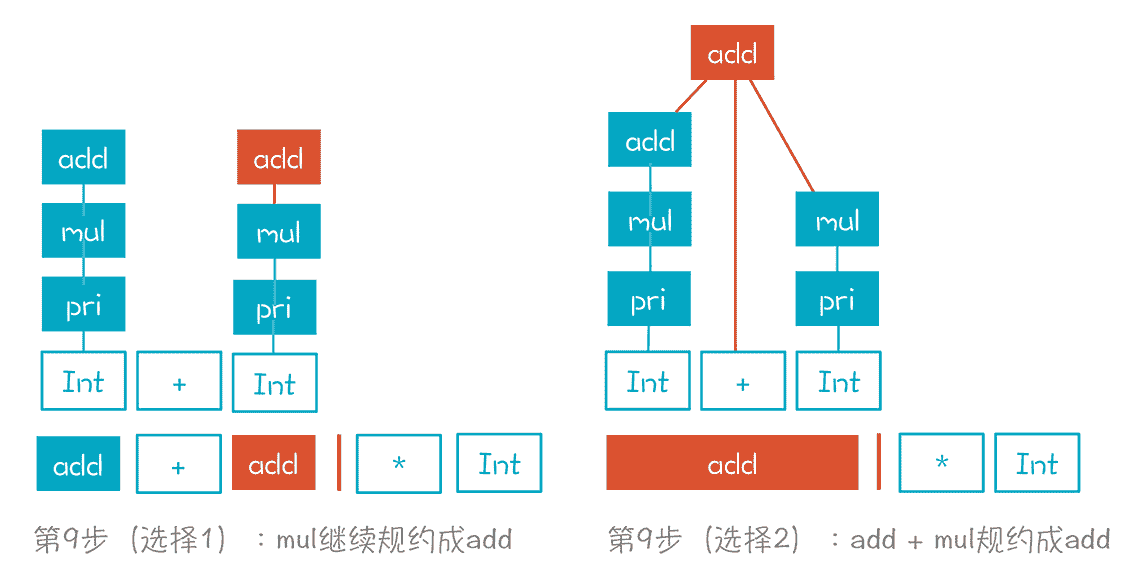
第三个选择,也就是按照“mul->mul*pri”,继续移进 * 号,而不是做规约。只有这样,才能形成正确的 AST,就像图中的虚线。
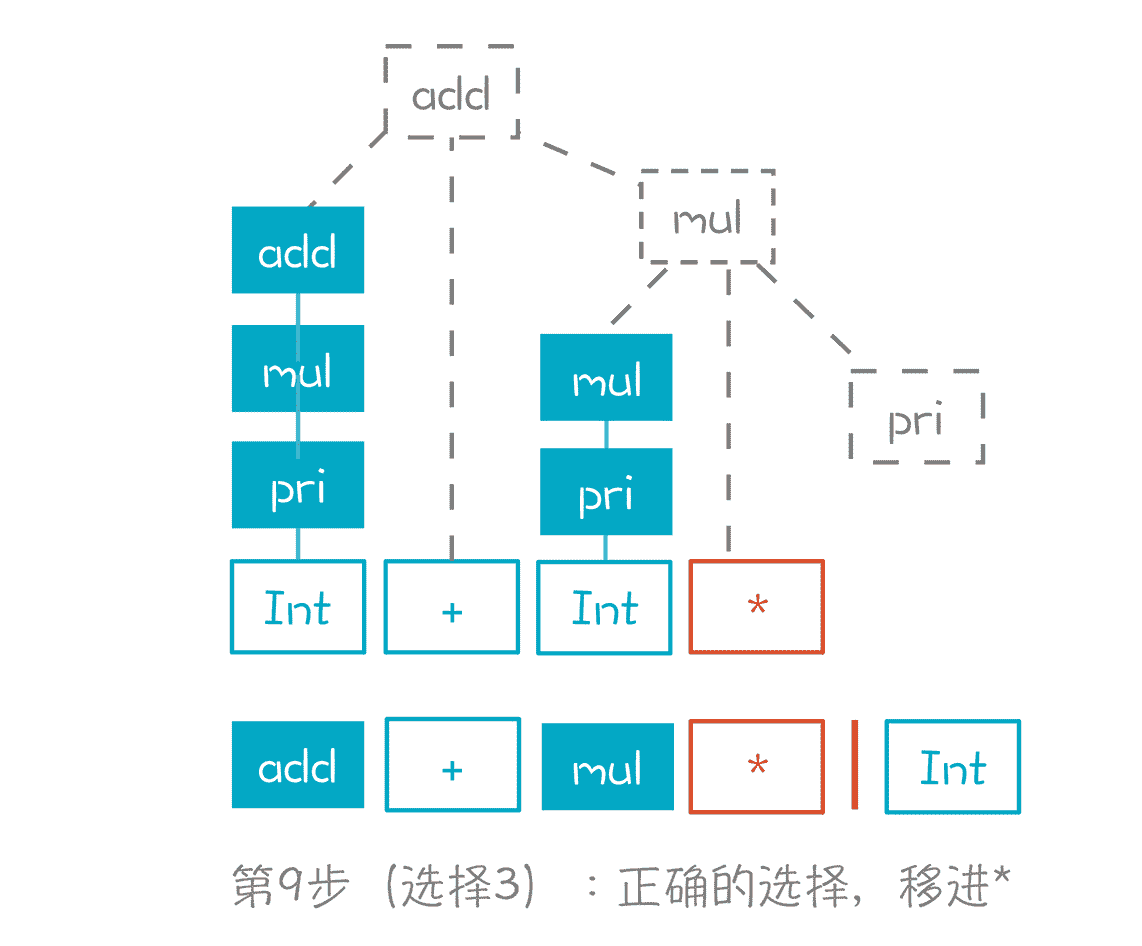
第 10 步,移进 Int,也就是数字 5。
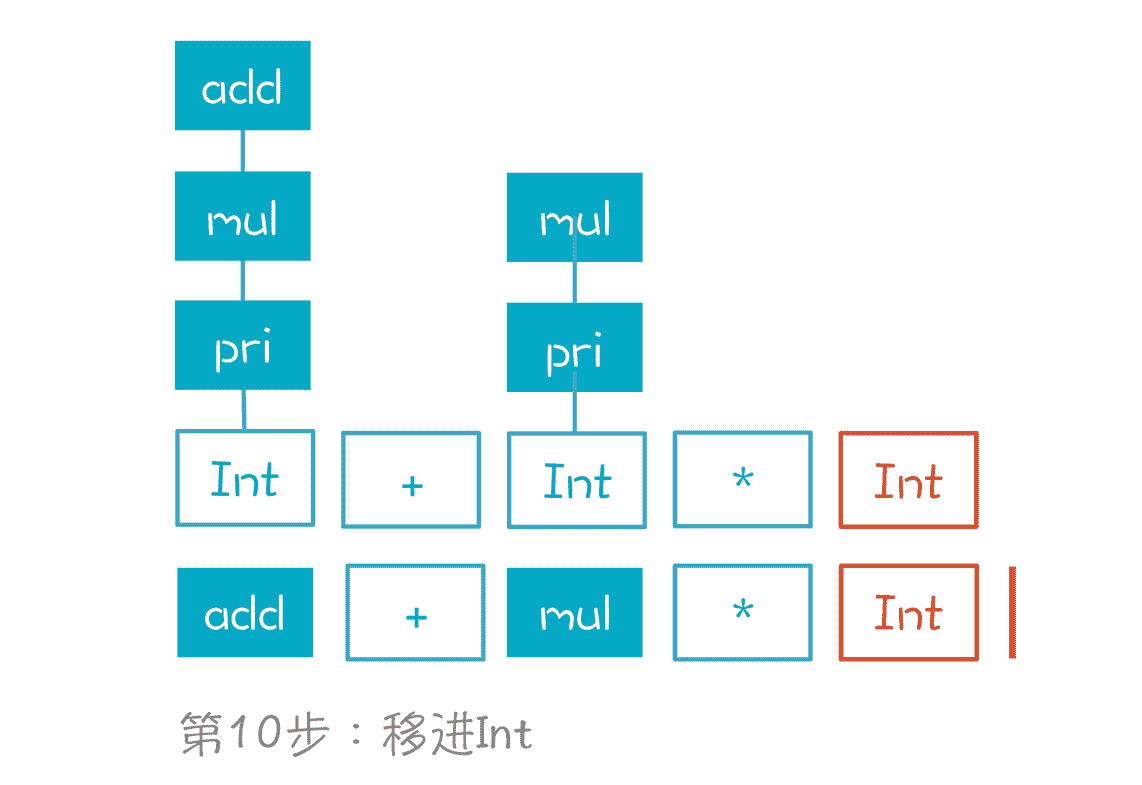
第 11 步,Int 规约成 pri。
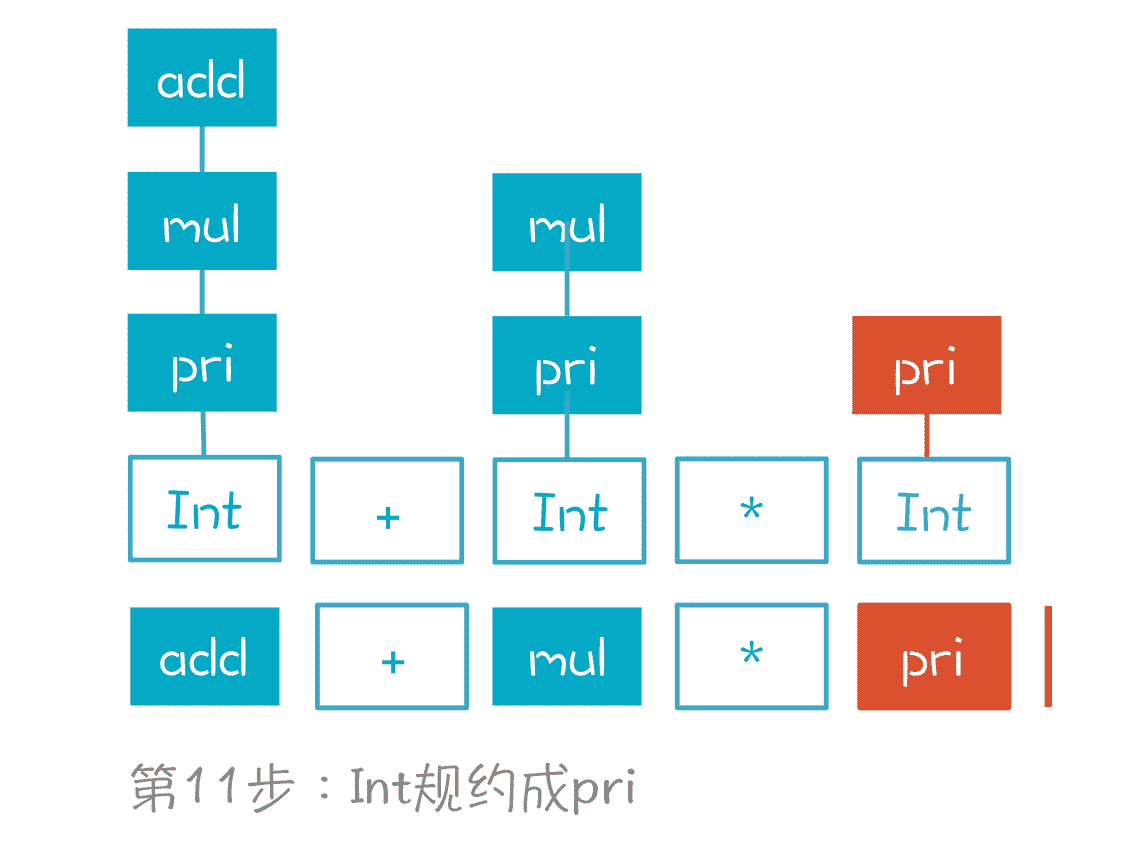
第 12 步,mul*pri 规约成 mul。
注意,这里也有两个选择,比如把 pri 继续规约成 mul。但它显然也是错误的选择。
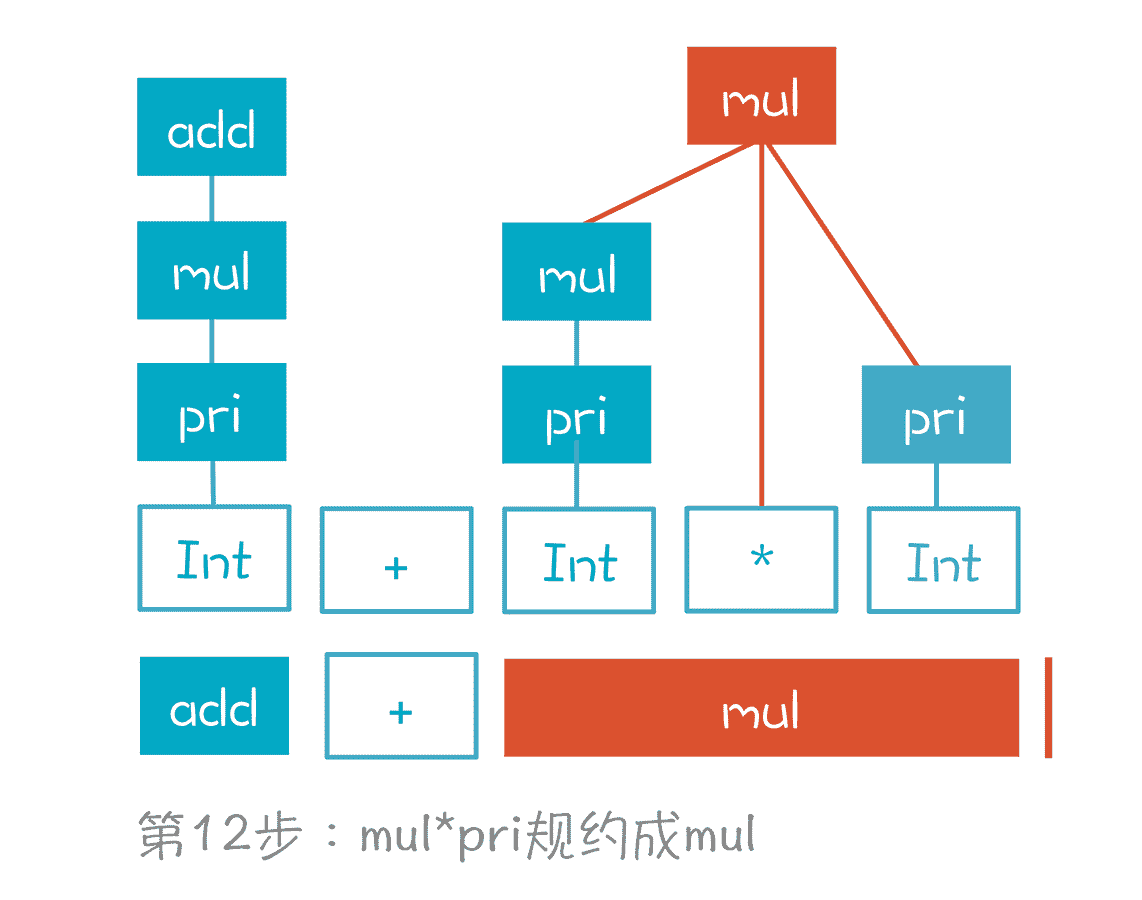
第 13 步,add+mul 规约成 add。
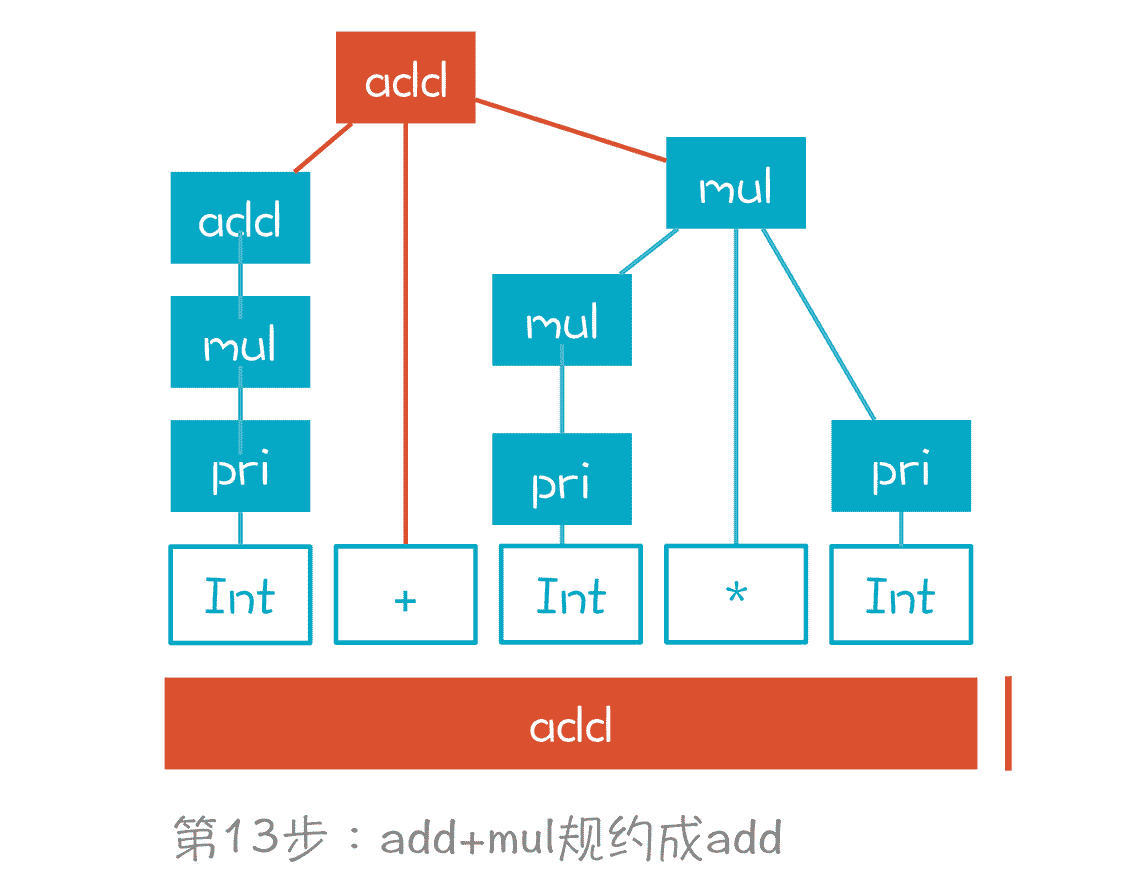
至此,我们就构建完成了一棵正确的 AST,并且,栈里也只剩下了一个元素,就是根节点。
整个语法解析过程,实质是**反向最右推导(Reverse RightMost Derivation)。**什么意思呢?如果把 AST 节点根据创建顺序编号,就是下面这张图呈现的样子,根节点编号最大是 13:
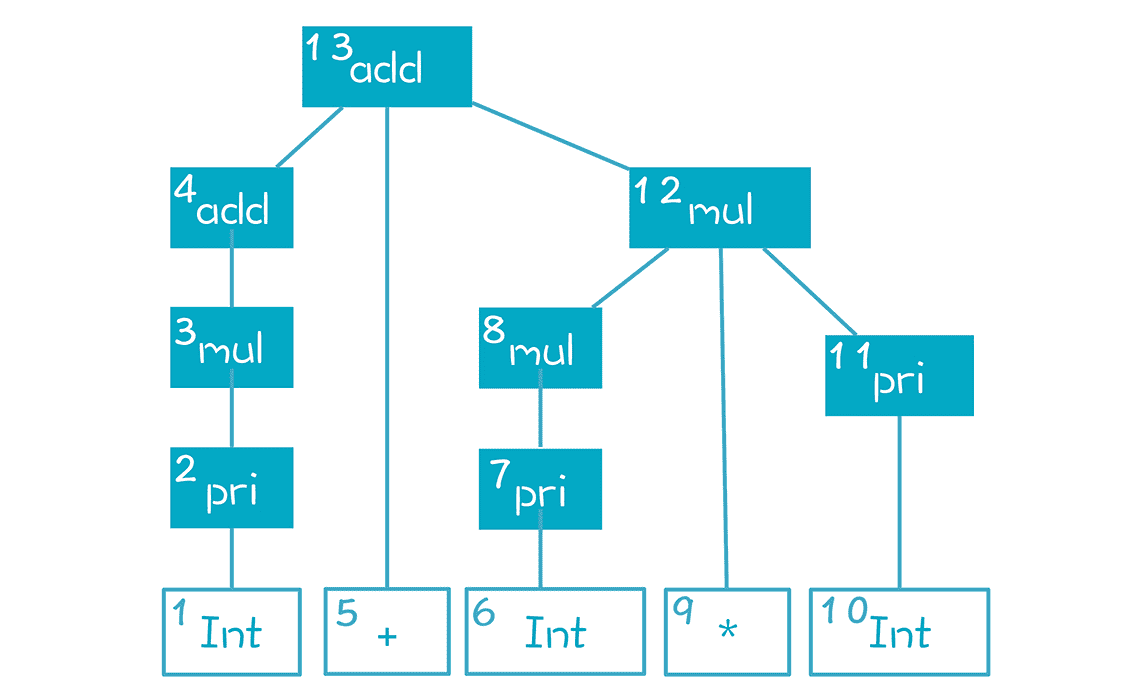
但这是规约的过程,如果是从根节点开始的推导过程,顺序恰好是反过来的,先是 13 号,再是右子节点 12 号,再是 12 号的右子节点 11 号,以此类推。我们把这个最右推导过程写在下面:

在语法解析的时候,我们是从底下反推回去,所以叫做反向的最右推导过程。从这个意义上讲,LR 算法中的 R,带有反向(Reverse)和最右(Reightmost)这两层含义。
在最右推导过程中,我加了下划线的部分,叫做一个句柄(Handle)。句柄是一个产生式的右边部分,以及它在一个右句型(最右推导可以得到的句型)中的位置。以最底下一行为例,这个句柄“Int”是产生式“pri->Int”的右边部分,它的位置是句型“Int + Int * Int”的第一个位置。
简单来说,句柄,就是产生式是在这个位置上做推导的,如果需要做反向推导的话,也是从这个位置去做规约。
针对这个简单的例子,我们可以用肉眼进行判断,找到正确的句柄,做出正确的选择。不过,要把这种判断过程变成严密的算法,做到在每一步都采取正确的行动,知道该做移进还是规约,做规约的话,按照哪个产生式,这就是 LR 算法要解决的核心问题了。
那么,如何找到正确的句柄呢?
找到正确的句柄
我们知道,最右推导是从最开始的产生式出发,经过多步推导(多步推导记做 ->*),一步步形成当前的局面(也就是左边栈里有一些非终结符和终结符,右边还可以预看 1 到 k 个 Token)。
|
|
我们要像侦探一样,根据手头掌握的信息,反向推导出这个多步推导的路径,从而获得正确的句柄。我们依据的是左边栈里的信息,以及右边的 Token 串。对于 LR(0) 算法来说,我们只依据左边的栈,就能找到正确的句柄,对于 LR(1) 算法来说,我们可以从右边预看一个 Token。
我们的思路是根据语法规则,复现这条推导路径。以第 8 步为例,下图是它的推导过程,橙色的路径是唯一能够到达第 8 步的路径。知道了正向推导的路径,自然知道接下来该做什么,在第 8 步,我们正确的选择是做移进。
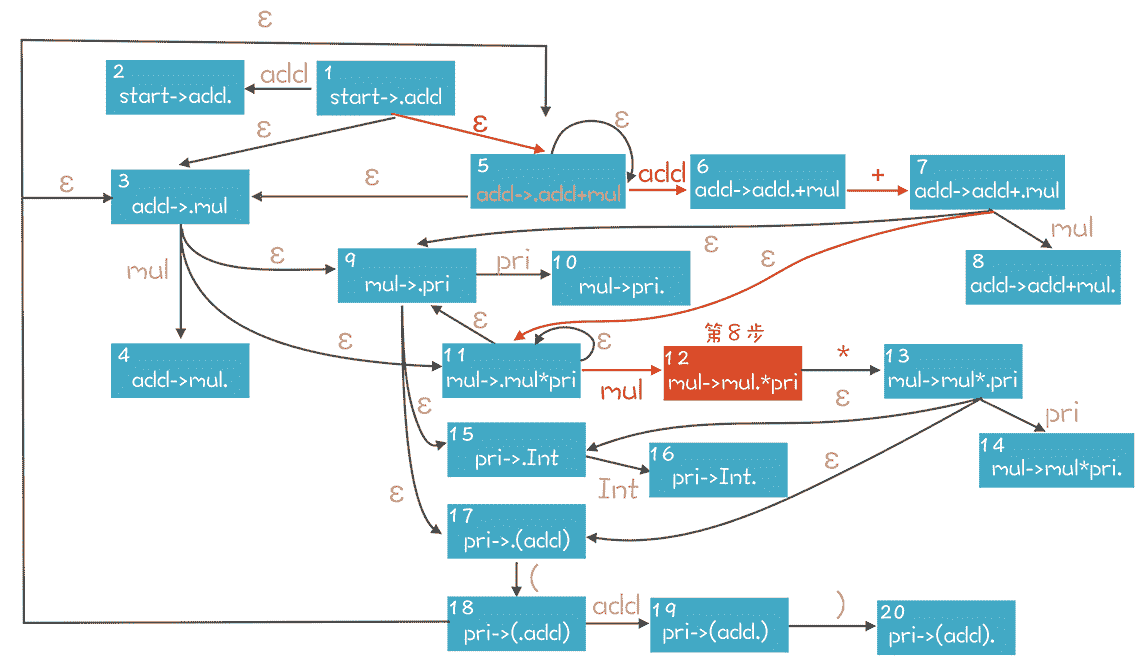
为了展示这个推导过程,我引入了一个新概念:项目(Item)。
Item 代表带有“.”符号的产生式。比如“pri->(add)”可以产生 4 个 Item,“.”分别在不同的位置。“.”可以看做是前面示意图中的竖线,左边的看做已经在栈里的部分,“.”右边的看做是期待获得的部分:
|
|
上图其实是一个 NFA,利用这个 NFA,我们表达了所有可能的推导步骤。每个 Item(或者状态),在接收到一个符号的时候,就迁移到下一个状态,比如“add->.add+mul”在接收到一个 add 的时候,就迁移到“add->add.+mul”,再接收到一个“+”,就迁移到“add->add+.mul”。
在这个状态图的左上角,我们用一个辅助性的产生式“start->add”,作为整个 NFA 的唯一入口。从这个入口出发,可以用这个 NFA 来匹配栈里内容,比如在第 8 步的时候,栈以及右边下一个 Token 的状态如下,其中竖线左边是栈的内容:
|
|
在 NFA 中,我们从 start 开始遍历,基于栈里的内容,能找到图中橙色的多步推导路径。在这个状态迁移过程中,导致转换的符号分别是“ε、add、+、ε、mul”,忽略其中的ε,就是栈里的内容。
在 NFA 中,我们查找到的 Item 是“mul->mul.*pri”。这个时候“.”在 Item 的中间。因此下一个操作只能是一个 Shift 操作,也就是把下一个 Token,* 号,移进到栈里。
如果“.”在 Item 的最后,则对应一个规约操作,比如在第 12 步,栈里的内容是:
|
|
这个时候的 Item 是“add->add+mul.”。对于所有点符号在最后面的 Item,我们已经没有办法继续向下迁移了,这个时候需要做一个规约操作,也就是基于“add + mul”规约到 add,也就是到“add->.add+mul”这个状态。对于任何的ε转换,其逆向操作也是规约,比如图中从“add->.add+mul”规约到“start->.add”。
但做规约操作之前,我们仍然需要检查后面跟着的 Token,是不是在 Follow(add) 中。对于 add 来说,它的 Follow 集合包括{$ + )}。如果是这些 Token,那就做规约。否则,就报编译错误。
所以,现在清楚了,我们能通过这个有限自动机,跟踪计算出正确的推导过程。
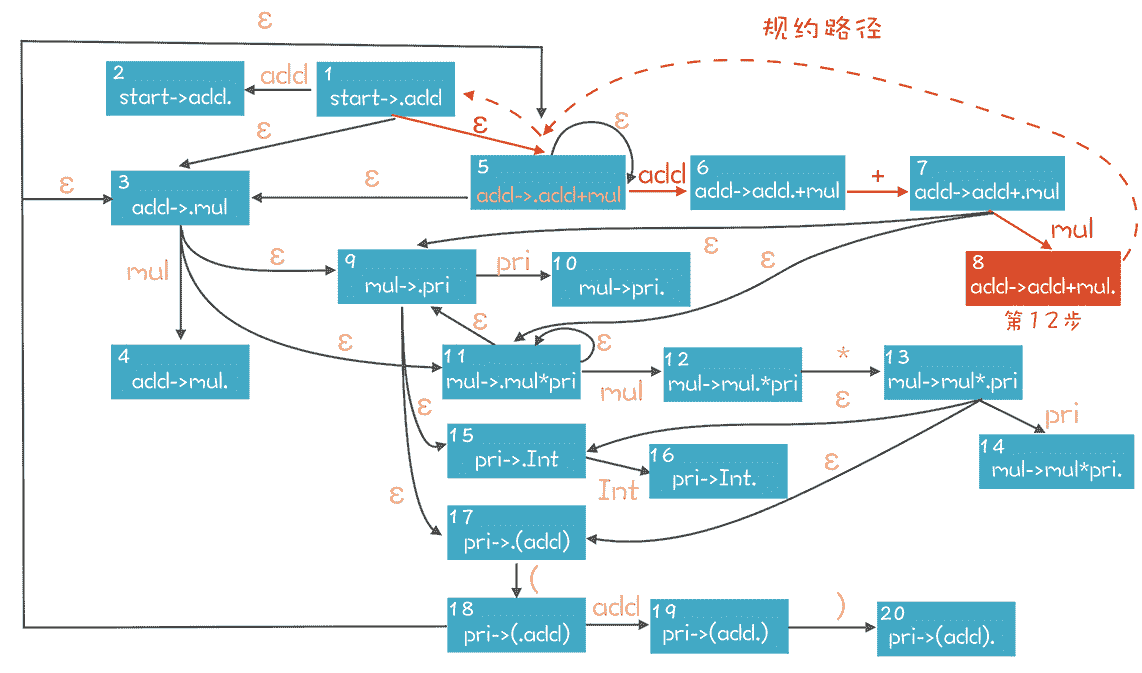
当然了,在16 讲里,我提到每个 NFA 都可以转换成一个 DFA。所以,你可以直接在上面的 NFA 里去匹配,也可以把 NFA 转成 DFA,避免 NFA 的回溯现象,让算法效率更高。转换完毕的 DFA 如下:
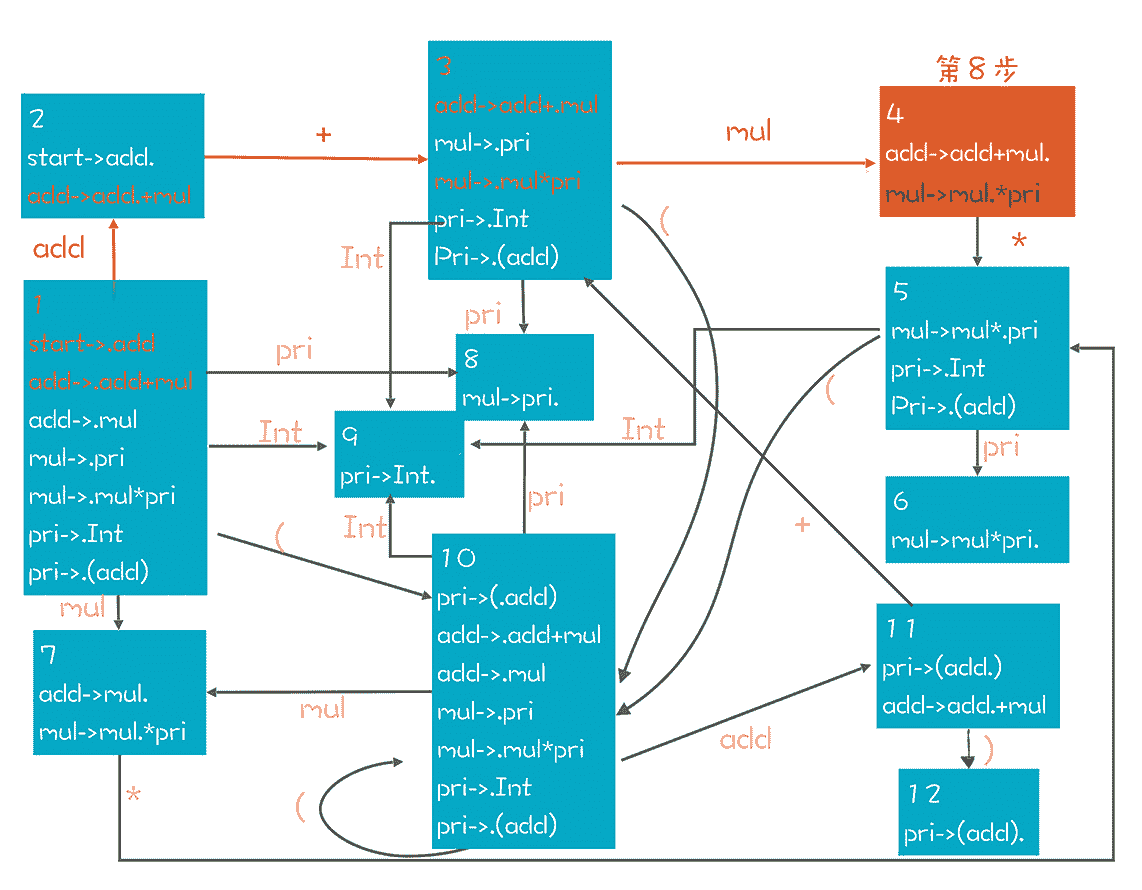
在这个 DFA 中,我同样标注了在第 8 步时的推导路径。
为了更清晰地理解 LR 算法的本质,我们基于这个 DFA 再把语法解析的过程推导一遍。
第 1 步,移进一个 Int,从状态 1 迁移到 9。Item 是“pri->Int.”。

第 2 步,依据“pri->Int”做规约,从状态 9 回到状态 1。因为现在栈里有个 pri 元素,所以又迁移进了状态 8。

第 3 步,依据“mul->pri”做规约,从状态 8 回到状态 1,再根据栈里的 mul 元素进入状态 7。**注意,**在状态 7 的时候,下一步的走向有两个可能的方向,分别是“add->mul.”和“mul->mul.*pri”这两个 Item 代表的方向。
基于“add->mul.”会做规约,而基于“mul->mul.*pri”会做移进,这就需要看看后面的 Token 了。如果后面的 Token 是 * 号,那其实要选第二个方向。但现在后面是 + 号,所以意味着这里只能做规约。
第 4 步,依据“add->mul”做规约,从状态 7 回到状态 1,再依据 add 元素进入状态 2。
第 5 步,移进 + 号。这对应状态图上的两次迁移,首先根据栈里的第一个元素 add,从 1 迁移到 2。然后再根据“+”,从 2 到 3。Item 的变化是:
状态 1:start->.add
状态 1:add->.add+mul
状态 2:add->add.+mul
状态 3:add->add+.mul
你看,通过移进这个加号,我们实际上知道了这个表达式顶部必然有一个“add+mul”的结构。
第 6 到第 8 步,移进 Int,并一直规约到 mul。状态变化是先从状态 3 到状态 9,然后回到状态 3,再进到状态 4。
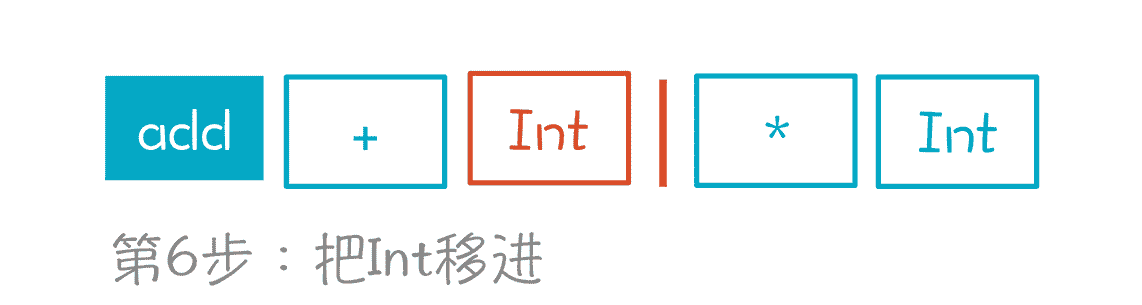

第 9 步,移进一个 *。根据栈里的元素,迁移路径是 1->2->3->4->5。

第 10 步,移进 Int,进入状态 9。
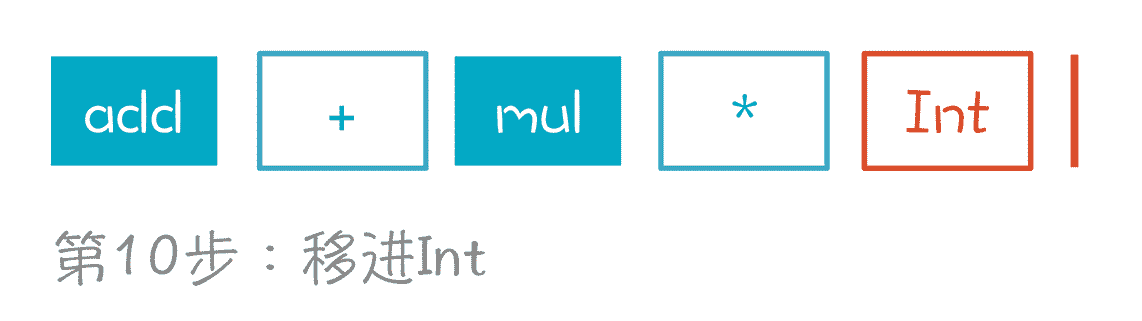
第 11 步,根据“pri->Int”规约到 pri,先退回到状态 5,接着根据 pri 进入状态 6。

第 12 步,根据“mul->mul*pri”规约到 mul,从而退回到状态 4。

第 13 步,根据“add->add+mul”规约到 add,从而退回到状态 2。

从状态 2 再根据“start->add”再规约一步,就变成了 start,回到状态 1,解析完成。
现在我们已经对整个算法的整个执行过程建立了直觉认知。如果想深入掌握 LR 算法,我建议你把这种推导过程多做几遍,自然会了然于胸。建立了直觉认知以后,接下来,我们再把 LR 算法的类型和实现细节讨论一下。
LR 解析器的类型和实现
LR 算法根据能力的强弱和实现的复杂程度,可以分成多个级别,分别是 LR(0)、SLR(k)(即简单 LR)、LALR(k)(Look ahead LR)和 LR(k),其中 k 表示要在 Token 队列里预读 k 个 Token。
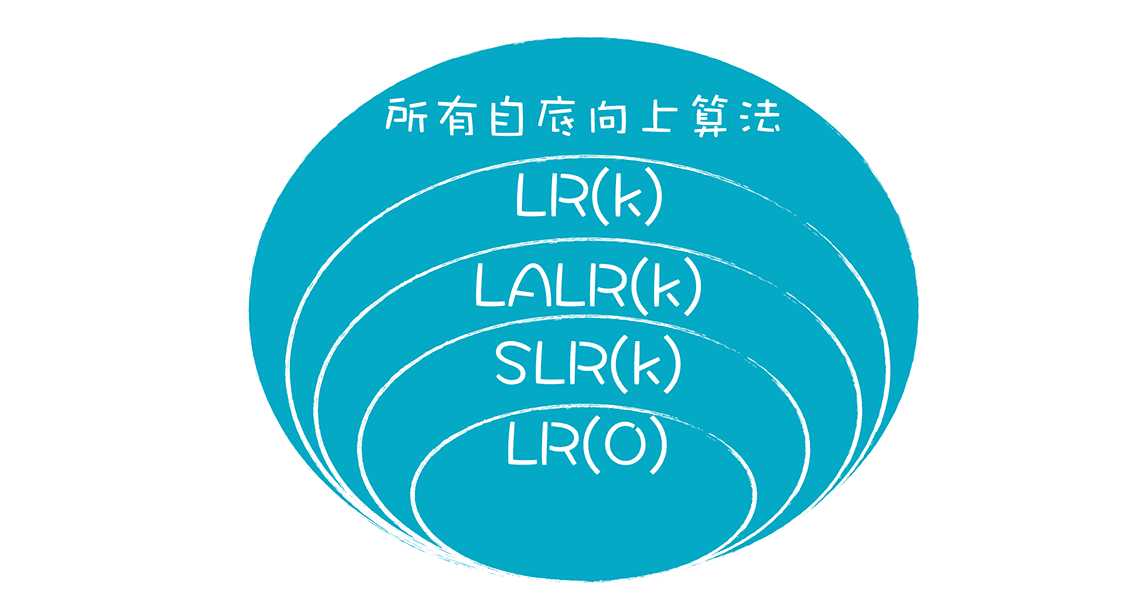
我来讲解一下这四种类型算法的特点,便于你选择和使用。
**LR(0) 不需要预看右边的 Token,仅仅根据左边的栈就能准确进行反向推导。**比如,前面 DFA 中的状态 8 只有一个 Item:“mul->pri.”。如果处在这个状态,那接下来操作是规约。假设存在另一个状态,它也只有一个 Item,点符号不在末尾,比如“mul->mul.*pri”,那接下来的操作就是移进,把下一个输入放到栈里。
但实际使用的语法规则很少有这么简单的。所以 LR(0) 的表达能力太弱,能处理的语法规则有限,不太有实用价值。就像在前面的例子中,如果我们不往下预读一个 Token,仅仅利用左边工作区的信息,是找不到正确的句柄的。
比如,在状态 7 中,我们可以做两个操作:
- 对于第一个 Item,“add->mul.”,需要做一个规约操作。
- 对于第二个 Item,“mul->mul.*pri”,实际上需要做一个移进操作。
这里发生的冲突,就叫做“移进 / 规约”冲突(Shift/Reduce Conflict)。意思是,又可以做移进,又可以做规约,到底做哪个?对于状态 7 来说,到底做哪个操作,实际上取决于右边的 Token。
**SLR(Simple LR)是在 LR(0) 的基础上做了增强。**对于状态 7 的这种情况,我们要加一个判断条件:右边下一个输入的 Token,是不是在 add 的 Follow 集合中。因为只有这样,做规约才有意义。
在例子中,add 的 Follow 集合是{+ ) $}。如果不在这个范围内,那么做规约肯定是不合法的。因为 Follow 集合的意思,就是哪些 Token 可以出现在某个非终结符后面。所以,如果在状态 7 中,下一个 Token 是 *,它不在 add 的 Follow 集合中,那么我们就只剩了一个可行的选择,就是移进。这样就不存在两个选择,也不存在冲突。
实际上,就我们本讲所用的示例语法而言,SLR 就足够了,但是对于另一些更复杂的语法,采用 SLR 仍然会产生冲突,比如:
|
|
这个语法说的是关于左值和右值的情况,我们曾在语义分析的时候说过。在这个语法里,右值只能出现在赋值符号右边。
在状态 2,如果下一个输入是“=”,那么做移进和规约都是可以的。因为“=”在 rvalue 的 Follow 集合中。
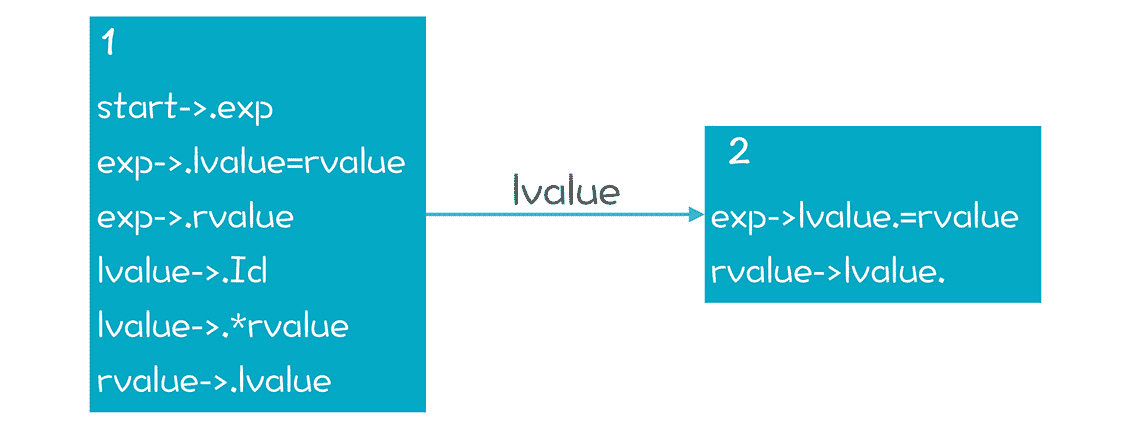
怎么来处理这种冲突呢?仅仅根据 Follow 集合来判断是否 Reduce,不太严谨。因为在上图状态 2 的情况下,即使后面跟着的是“=”,我们仍然不能做规约。因为你一规约,就成了一个右值,但它在等号的左边,显然是跟我们的语法定义冲突的。
办法是 Follow 集合拆了,把它的每个成员都变成 Item 的一部分。这样我们就能做更细致的判断。如下图所示,这样细化以后,我们发现在状态 2 中,只有下一个输入是“$”的时候,才能做规约。这就是 LR(1) 算法的原理,它更加强大。

但 LR(1) 算法也有一个缺点,就是 DFA 可能会很大。在语法分析阶段,DFA 的大小会随着语法规则的数量呈指数级上升,一个典型的语言的 DFA 状态可能达到上千个,这会使语法分析的性能很差,从而也丧失了实用性。
**LALR(k) 是基于这个缺点做的改进。**它用了一些技巧,能让状态数量变得比较少,但处理能力没有太大的损失。YACC 和 Bison 这两个工具,就是基于 LALR(1) 算法的。
课程小结
今天,我们讲了自底向上的 LR 算法的原理,包括移进 - 规约,如何寻找正确的句柄,如果基于 NFA 和 DFA 决定如何做移进和规约。
LR 算法是公认的比较难学的一个算法。好在我们已经在前两讲给它做了技术上的铺垫了,包括 NFA 和 DFA,First 和 Follow 集合。这节课我们重点在于建立直观理解,特别是如何依据栈里的信息做正确的反推。这个直觉认知很重要,建立这个直觉的最好办法,就是像本节课一样,根据实例来画图、推导。这样,在你真正动手写算法的时候,就胸有成竹了!
到今天为止,我们已经把前端技术中的关键算法都讲完了。**不过我还是想强调一下,**如果想真正掌握这些算法,必须动手实现一下才行,勤动手才是王道。
一课一思
在讲自顶向下的算法时,我提到,递归思维是重要的计算机科学思维方式。而自底向上的方法,也是另一种重要的思维方式。那么,请结合你的经验,思考一下在你的领域内,是否有一些问题,用自底向上的方法能更好地解决。LR 算法的移进 - 规约思想,能否在解决其他自底向上的问题中发挥作用?欢迎在留言区分享你的经验和思考。
最后,感谢你的阅读,如果这篇文章让你有所收获,也欢迎你将它分享给更多的朋友。
本节课的示例代码我放在了文末,供你参考。

文章作者
上次更新 2025-01-03