02_词法分析:用两种方式构造有限自动机
文章目录
你好,我是宫文学。
上一讲,我带你把整个编译过程走了一遍。这样,你就知道了编译过程的整体步骤,每一步是做什么的,以及为什么要这么做。
进一步地,你就可以研究一下每个环节具体是如何实现的、有哪些难点、有哪些理论和算法。通过这个过程,你不仅可以了解每个环节的原理,还能熟悉一些专有词汇。这样一来,你在读编译原理领域的相关资料时,就会更加顺畅了。
不过,编译过程中涉及的算法和原理有些枯燥,所以我会用尽量通俗、直观的方式来给你解读,让你更容易接受。
本讲,我主要跟你讨论一下词法分析(Lexical Analysis)这个环节。通过这节课,你可以掌握词法分析这个阶段是如何把字符串识别成一个个 Token 的。进而,你还会学到如何实现一个正则表达式工具,从而实现任意的词法解析。
词法分析的原理
首先,我们来了解一下词法分析的原理。
通过上一讲,你已经很熟悉词法分析的任务了:输入的是字符串,输出的是 Token 串。所以,词法分析器在英文中一般叫做 Tokenizer。
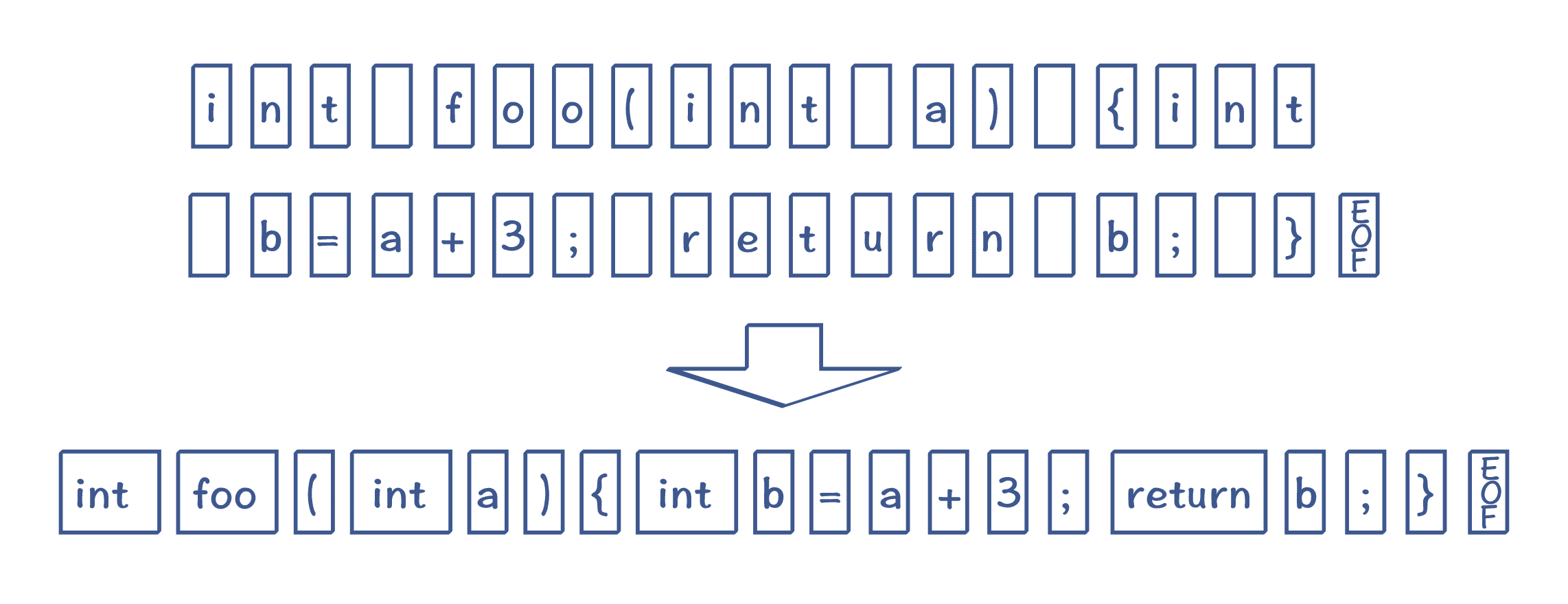
图 1:把字符串转换为 Token(注意:其中的空白字符,代表空格、tab、回车和换行符,EOF 是文件结束符)
但具体如何实现呢?这里要有一个计算模型,叫做有限自动机(Finite-state Automaton,FSA),或者叫做有限状态自动机(Finite-state Machine,FSM)。
有限自动机这个名字,听上去可能比较陌生。但大多数程序员,肯定都接触过另一个词:状态机。假设你要做一个电商系统,那么订单状态的迁移,就是一个状态机。
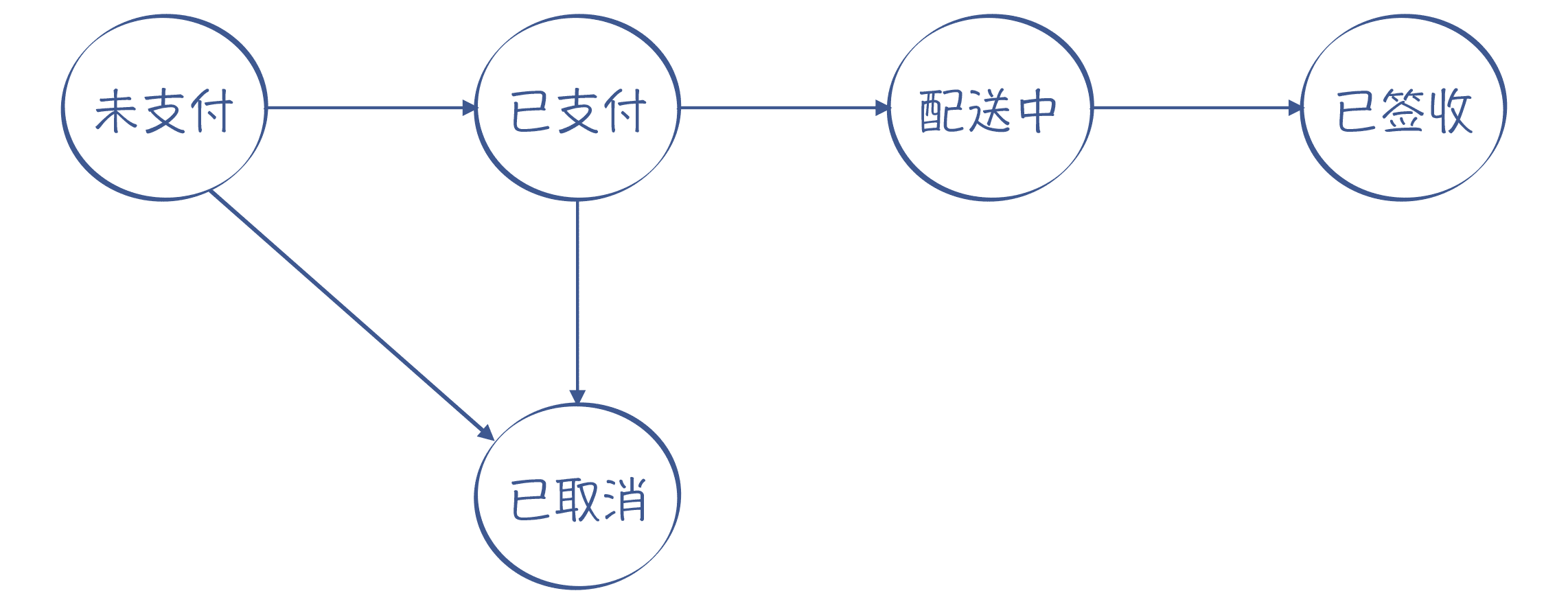
图 2:状态机的例子(订单的状态和迁移过程)
有限自动机就是这样的状态机,它的状态数量是有限的。当它收到一个新字符的时候,会导致状态的迁移。比如说,下面的这个状态机能够区分标识符和数字字面量。

图 3:一个能够识别标识符和数字字面量的有限自动机
在这样一个状态机里,我用单线圆圈表示临时状态,双线圆圈表示接受状态。接受状态就是一个合格的 Token,比如图 3 中的状态 1(数字字面量)和状态 2(标识符)。当这两个状态遇到空白字符的时候,就可以记下一个 Token,并回到初始态(状态 0),开始识别其他 Token。
可以看出,**词法分析的过程,其实就是对一个字符串进行模式匹配的过程。**说起字符串的模式匹配,你能想到什么工具吗?对的,正则表达式工具。
大多数语言,以及一些操作系统的命令,都带有正则表达式工具,来帮助你匹配合适的字符串。比如下面的这个 Linux 命令,可以用来匹配所有包含“sa”“sb” … “sh”字符串的进程。
ps -ef | grep ’s[a-h]'
在这个命令里,“s[a-h]”是用来描述匹配规则的,我们把它叫做一个正则表达式。
同样地,正则表达式也可以用来描述词法规则。这种描述方法,我们叫做正则文法(Regular Grammar)。比如,数字字面量和标识符的正则文法描述是这样的:
IntLiteral : [0-9]+; //至少有一个数字
Id : [A-Za-z][A-Za-z0-9]*; //以字母开头,后面可以是字符或数字
与普通的正则表达式工具不同的是,词法分析器要用到很多个词法规则,每个词法规则都采用**“Token 类型:正则表达式”**这样一种格式,用于匹配一种 Token。
然而,当我们采用了多条词法规则的时候,有可能会出现词法规则冲突的情况。比如说,int 关键字其实也是符合标识符的词法规则的。
Int : int; //int 关键字
For : for; //for 关键字
Id : [A-Za-z][A-Za-z0-9]*; //以字母开头,后面可以是字符或数字
所以,词法规则里面要有优先级,比如排在前面的词法规则优先级更高。这样的话,我们就能够设计出区分 int 关键字和标识符的有限自动机了,可以画成下面的样子。其中,状态 1、2 和 3 都是标识符,而状态 4 则是 int 关键字。

图 4:一个能够识别 int 关键字和标识符的有限自动机
从正则表达式生成有限自动机
现在,你已经了解了如何构造有限自动机,以及如何处理词法规则的冲突。基本上,你就可以按照上面的思路来手写词法分析器了。但你可能觉得,这样手写词法分析器的步骤太繁琐了,我们能否只写出词法规则,就自动生成相对应的有限自动机呢?
当然是可以的,实际上,正则表达式工具就是这么做的。此外,词法分析器生成工具 lex(及 GNU 版本的 flex)也能够基于规则自动生成词法分析器。
它的具体实现思路是这样的:**把一个正则表达式翻译成 NFA,然后把 NFA 转换成 DFA。**对不起,我这里又引入了两个新的术语:NFA 和 DFA。
先说说 DFA,它是“Deterministic Finite Automaton”的缩写,即确定的有限自动机。它的特点是:该状态机在任何一个状态,基于输入的字符,都能做一个确定的状态转换。前面例子中的有限自动机,都属于 DFA。
再说说 NFA,它是“Nondeterministic Finite Automaton”的缩写,即不确定的有限自动机。它的特点是:该状态机中存在某些状态,针对某些输入,不能做一个确定的转换。
这又细分成两种情况:
- 对于一个输入,它有两个状态可以转换。
- 存在ε转换的情况,也就是没有任何字符输入的情况下,NFA 也可以从一个状态迁移到另一个状态。
比如,“a[a-zA-Z0-9]*bc”这个正则表达式,对字符串的要求是以 a 开头,以 bc 结尾,a 和 bc 之间可以有任意多个字母或数字。可以看到,在图 5 中,状态 1 的节点输入 b 时,这个状态是有两条路径可以选择的:一条是迁移到状态 2,另一条是仍然保持在状态 1。所以,这个有限自动机是一个 NFA。
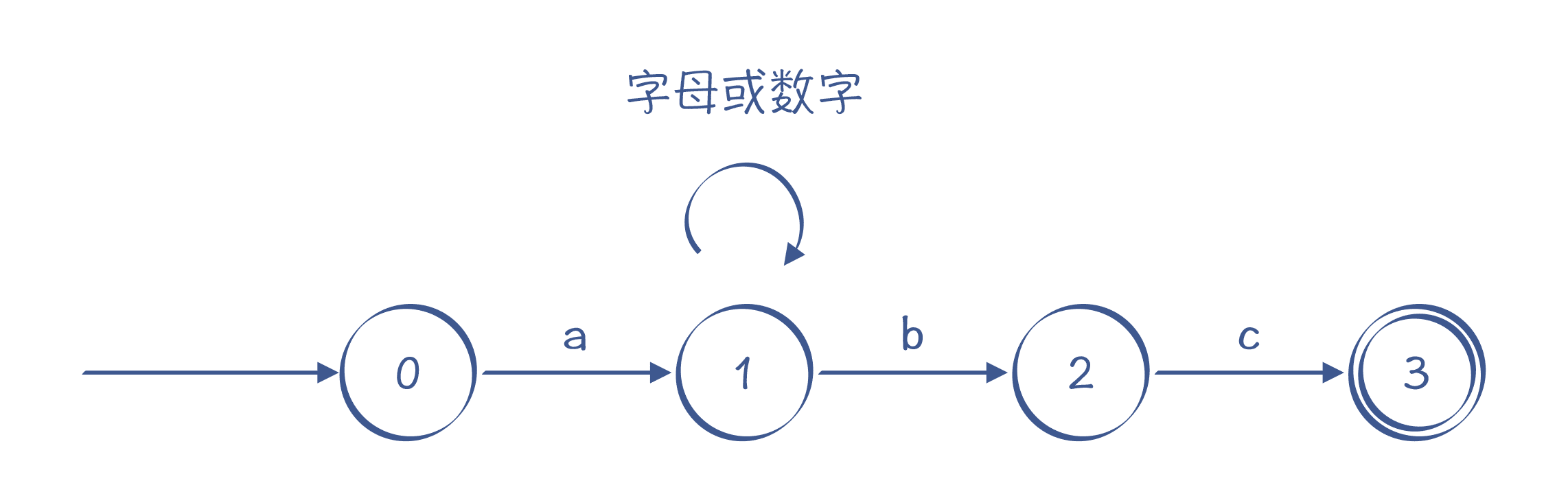
图 5:一个 NFA 的例子,识别“a[a-zA-Z0-9]*bc”的自动机
这个 NFA 还有引入ε转换的画法,如图 6 所示,它跟图 5 的画法是等价的。实际上,图 6 表示的 NFA 可以用我们下面马上要讲到的算法,通过正则表达式自动生成出来。
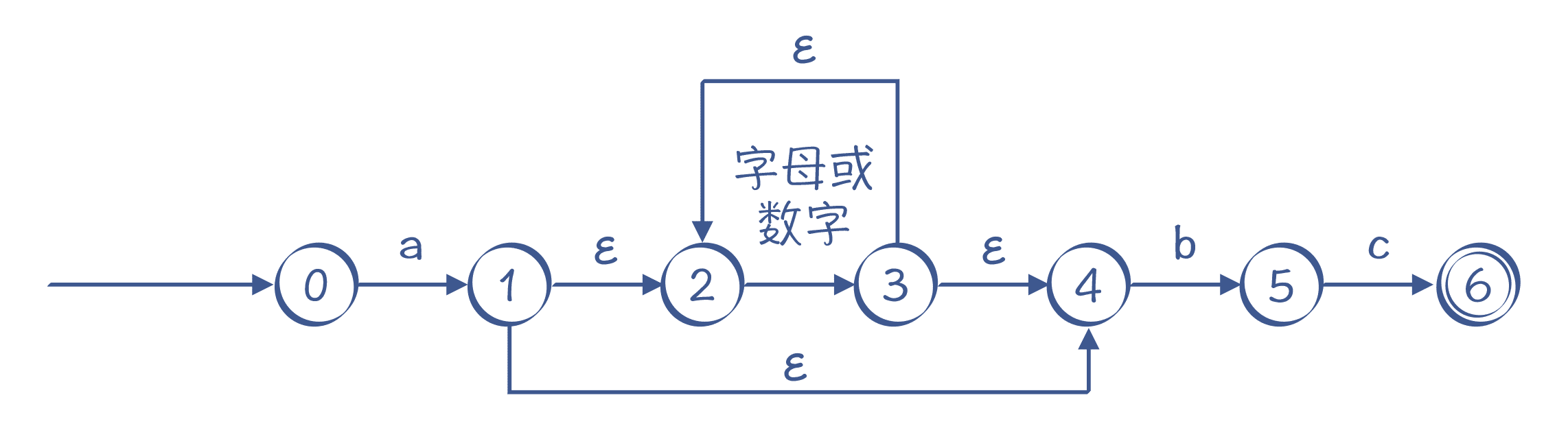
图 6:另一个 NFA 的例子,同样能识别“a[a-zA-Z0-9]*bc”,其中有ε转换
需要注意的是,无论是 NFA 还是 DFA,都等价于正则表达式。也就是说,所有的正则表达式都能转换成 NFA 或 DFA;而所有的 NFA 或 DFA,也都能转换成正则表达式。
理解了 NFA 和 DFA 以后,接下来我再大致说一下算法。
首先,一个正则表达式可以机械地翻译成一个 NFA。它的翻译方法如下:
- 识别字符 i 的 NFA。
当接受字符 i 的时候,引发一个转换,状态图的边上标注 i。其中,第一个状态(i,initial)是初始状态,第二个状态 (f,final) 是接受状态。

图 7:识别 i 的 NFA
- 转换“s|t”这样的正则表达式。
它的意思是,或者 s,或者 t,二者选一。s 和 t 本身是两个子表达式,我们可以增加两个新的状态:开始状态和接受状态。然后,用ε转换分别连接代表 s 和 t 的子图。它的含义也比较直观,要么走上面这条路径,那就是 s,要么走下面这条路径,那就是 t:
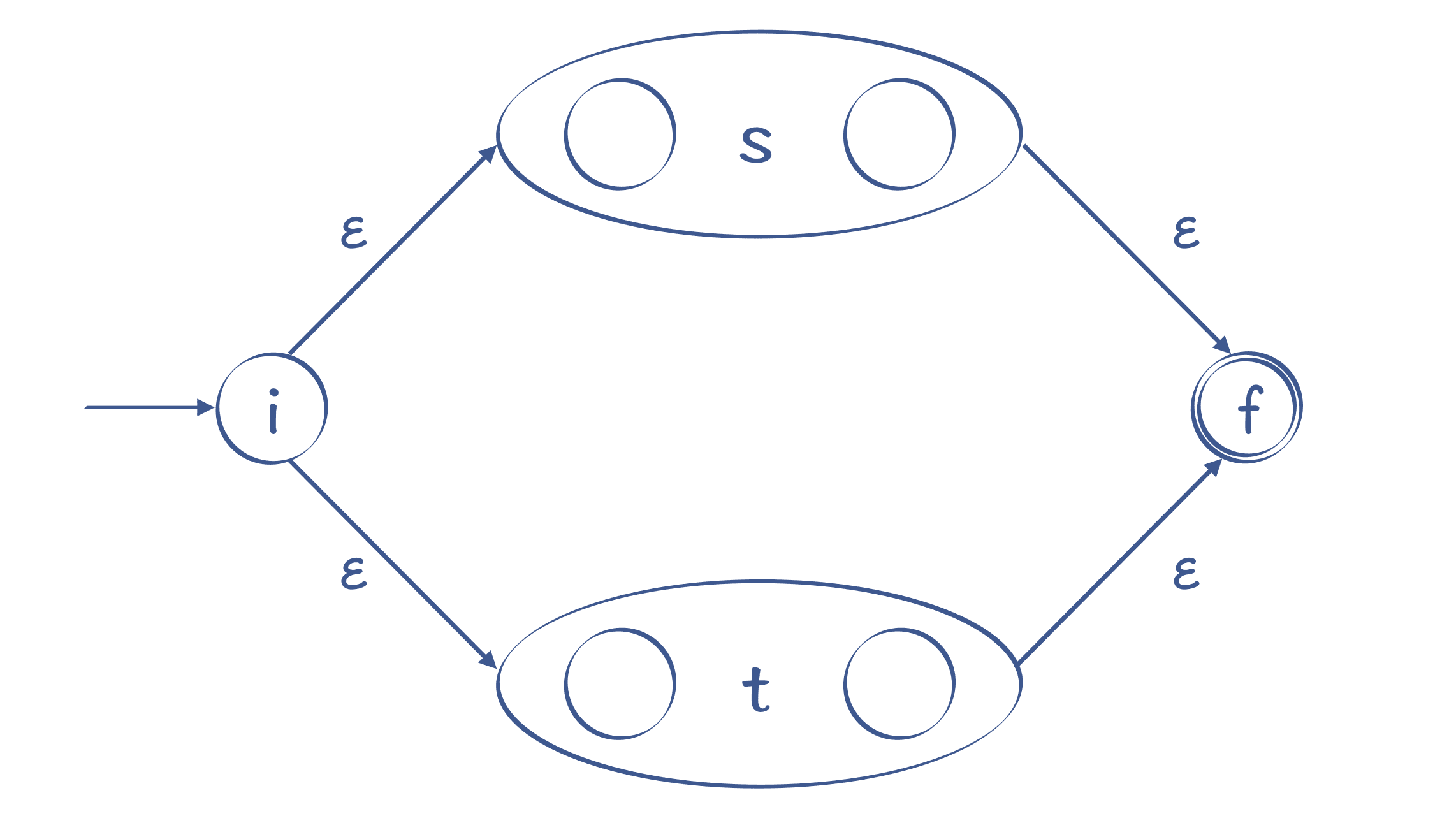
图 8:识别 s|t 的 NFA
- 转换“st”这样的正则表达式。
s 之后接着出现 t,转换规则是把 s 的开始状态变成 st 整体的开始状态,把 t 的结束状态变成 st 整体的结束状态,并且把 s 的结束状态和 t 的开始状态合二为一。这样就把两个子图衔接了起来,走完 s 接着走 t。

图 9:识别 st 的 NFA
- 对于“?”“*”和“+”这样的符号,它们的意思是可以重复 0 次、0 到多次、1 到多次,转换时要增加额外的状态和边。以“s*”为例,我们可以做下面的转换:
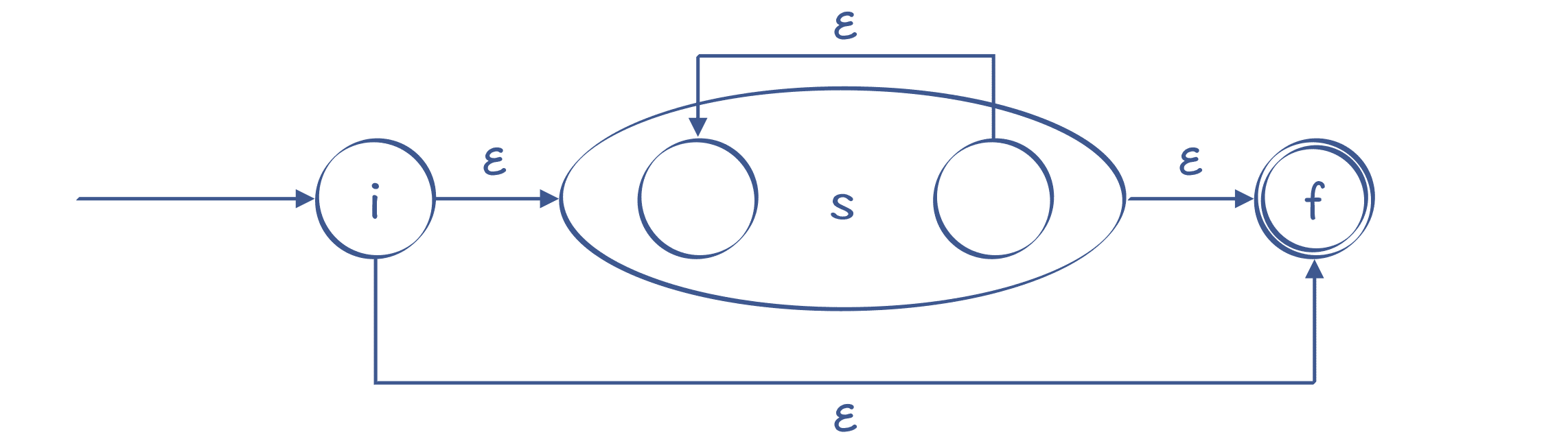
图 10:识别 s* 的 NFA
你能看出,它可以从 i 直接到 f,也就是对 s 匹配 0 次,也可以在 s 的起止节点上循环多次。
如果是“s+”,那就没有办法跳过 s,s 至少要经过一次:
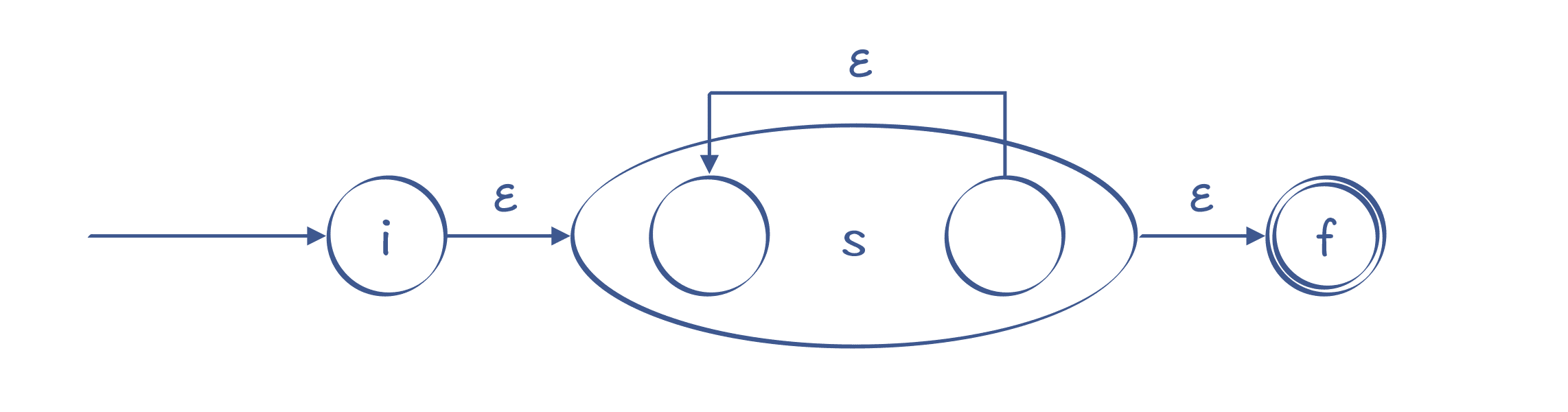
图 11:识别 s+ 的 NFA
通过这样的转换,所有的正则表达式,都可以转换为一个 NFA。
基于 NFA,你仍然可以实现一个词法分析器,只不过算法会跟基于 DFA 的不同:当某个状态存在一条以上的转换路径的时候,你要先尝试其中的一条;如果匹配不上,再退回来,尝试其他路径。这种试探不成功再退回来的过程,叫做回溯(Backtracking)。
小提示:下一讲的递归下降算法里,也会出现回溯现象,你可以对照着理解。
基于 NFA,你也可以写一个正则表达式工具。实际上,我在示例程序中已经写了一个简单的正则表达式工具,使用了Regex.java中的 regexToNFA 方法。如下所示,我用了一个测试用的正则表达式,它能识别 int 关键字、标识符和数字字面量。在示例程序中,这个正则表达式首先被表示为一个内部的树状数据结构,然后可以转换成 NFA。
int | [a-zA-Z][a-zA-Z0-9]* | [0-9]*
示例程序也会将生成的 NFA 打印输出,下面的输出结果中列出了所有的状态,以及每个状态到其他状态的转换,比如“0 ε -> 2”的意思是从状态 0 通过 ε 转换,到达状态 2:
NFA states:
0 ε -> 2
ε -> 8
ε -> 14
2 i -> 3
3 n -> 5
5 t -> 7
7 ε -> 1
1 (end)
acceptable
8 [a-z]|[A-Z] -> 9
9 ε -> 10
ε -> 13
10 [0-9]|[a-z]|[A-Z] -> 11
11 ε -> 10
ε -> 13
13 ε -> 1
14 [0-9] -> 15
15 ε -> 14
ε -> 1
我用图片来直观展示一下输出结果,分为上、中、下三条路径,你能清晰地看出解析 int 关键字、标识符和数字字面量的过程:
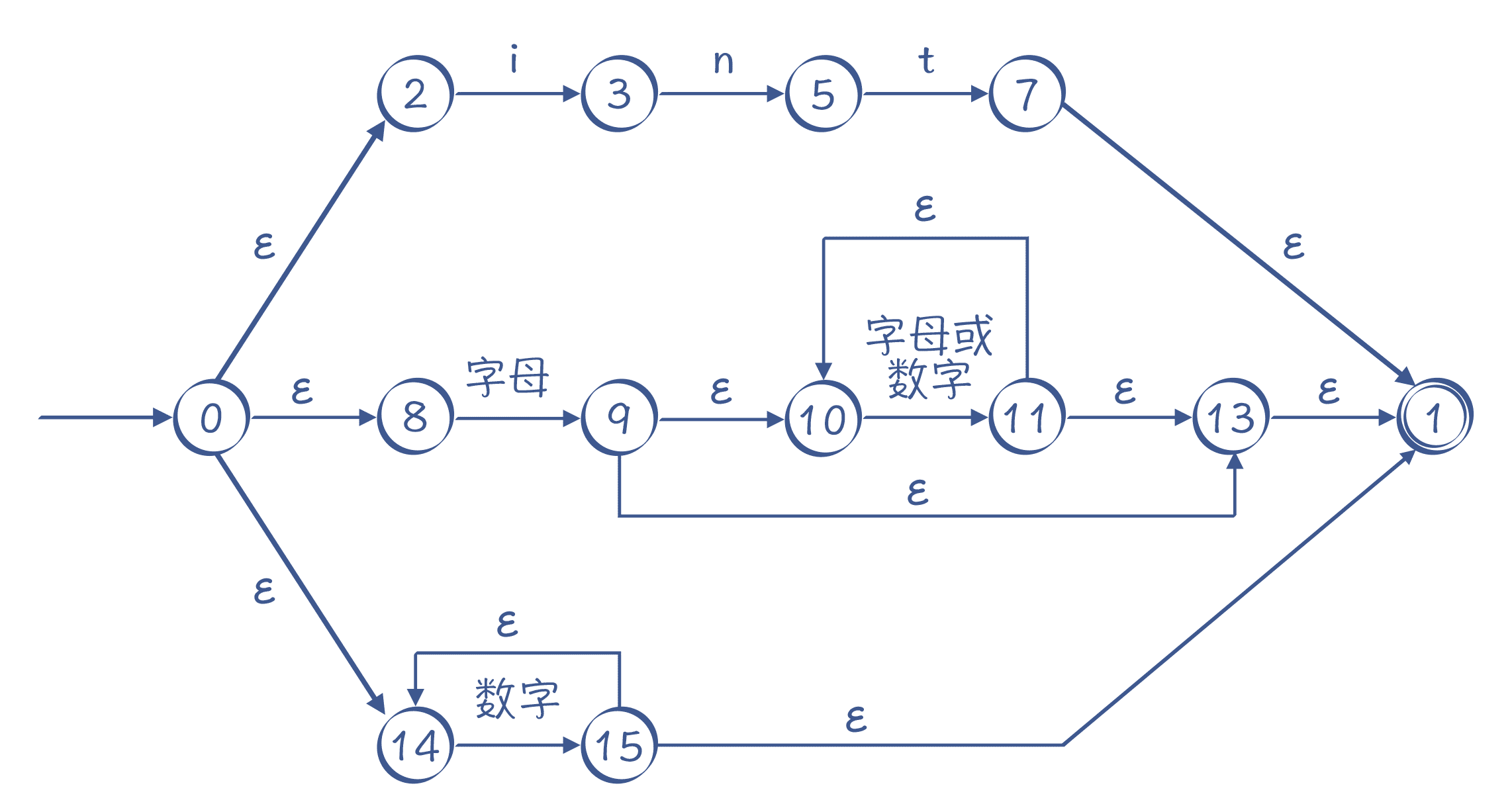
图 12:由算法自动生成的 NFA
那么生成 NFA 之后,我们要如何利用它,来识别某个字符串是否符合这个 NFA 代表的正则表达式呢?
还是以图 12 为例,当我们解析“intA”这个字符串时,首先选择最上面的路径进行匹配,匹配完 int 这三个字符以后,来到状态 7,若后面没有其他字符,就可以到达接受状态 1,返回匹配成功的信息。
**可实际上,int 后面是有 A 的,所以第一条路径匹配失败。**失败之后不能直接返回“匹配失败”的结果,因为还有其他路径,所以我们要回溯到状态 0,去尝试第二条路径,在第二条路径中,我们尝试成功了。
运行 Regex.java 中的 matchWithNFA() 方法,你可以用 NFA 来做正则表达式的匹配。其中,在匹配“intA”时,你会看到它的回溯过程:
NFA matching: ‘intA’
trying state : 0, index =0
trying state : 2, index =0 //先走第一条路径,即 int 关键字这个路径
trying state : 3, index =1
trying state : 5, index =2
trying state : 7, index =3
trying state : 1, index =3 //到了末尾,发现还有字符’A’没有匹配上
trying state : 8, index =0 //回溯,尝试第二条路径,即标识符
trying state : 9, index =1
trying state : 10, index =1 //在 10 和 11 这里循环多次
trying state : 11, index =2
trying state : 10, index =2
trying state : 11, index =3
trying state : 10, index =3
true
从中你可以看到用 NFA 算法的特点:因为存在多条可能的路径,所以需要试探和回溯,在比较极端的情况下,回溯次数会非常多,性能会变得非常差。特别是当处理类似“s*”这样的语句时,因为 s 可以重复 0 到无穷次,所以在匹配字符串时,可能需要尝试很多次。
NFA 的运行可能导致大量的回溯,**那么能否将 NFA 转换成 DFA,让字符串的匹配过程更简单呢?**如果能的话,那整个过程都可以自动化,从正则表达式到 NFA,再从 NFA 到 DFA。
方法是有的,这个算法就是子集构造法。不过我这里就不展开介绍了,如果你想继续深入学习的话,可以去看看本讲最后给出的参考资料。
总之,只要有了准确的正则表达式,是可以根据算法自动生成对字符串进行匹配的程序的,这就是正则表达式工具的基本原理,也是有些工具(比如 ANTLR 和 flex)能够自动给你生成一个词法分析器的原理。
课程小结
本讲涵盖了词法分析所涉及的主要知识点。词法分析跟你日常使用的正则表达式关系很密切,你可以用正则表达式来表示词法规则。
在实际的编译器中,词法分析器一般都是手写的,依据的基本原理就是构造有限自动机。不过有一些地方也会用手工编码的方式做一些优化(如 javac 编译器),有些编译器会做用一些特别的技巧来提升解析速度(如 JavaScript 的 V8 编译器),你在后面的课程中会看到。
基于正则表达式构造 NFA,再去进行模式匹配,是一个很好的算法思路,它不仅仅可以用于做词法分析,其实还可以用于解决其他问题(比如做语法分析),值得你去做举一反三的思考。
一课一思
你可以试着写出识别整型字面量和浮点型字面量的词法规则,手工构造一个有限自动机。
欢迎在留言区谈谈你的实践体会,也欢迎你把今天的内容分享给更多的朋友。
参考资料
关于从 NFA 转 DFA 的算法,你可以参考 _Compilers - Principles, Techniques & Tools_(龙书,第 2 版)第 3.7.1 节,或者《编译原理之美》的第 16 讲。
文章作者
上次更新 2025-01-03