14_Java_JIT编译器(二):Sea_of_Nodes为何如此强大?
文章目录
你好,我是宫文学。这一讲,我们继续来研究 Graal 编译器,重点来了解一下它的 IR 的设计。
在上一讲中,我们发现 Graal 在执行过程中,创建了一个图的数据结构,这个数据结构就是 Graal 的 IR。之后的很多处理和优化算法,都是基于这个 IR 的。可以说,这个 IR 是 Graal 编译器的核心特性之一。
那么,为什么这个 IR 采用的是图结构?它有什么特点和优点?编译器的优化算法又是如何基于这个 IR 来运行的呢?
今天,我就带你一起来攻破以上这些问题。在揭晓问题答案的过程中,你对真实编译器中 IR 的设计和优化处理过程,也就能获得直观的认识了。
基于图的 IR
IR 对于编译器非常重要,因为它填补了高级语言和机器语言在语义上的巨大差别。比如说,你在高级语言中是使用一个数组,而翻译成最高效的 x86 机器码,是用间接寻址的方式,去访问一块连续的内存。所以 IR 的设计必须有利于实现这种转换,并且还要有利于运行优化算法,使得生成的代码更加高效。
在上一讲中,通过跟踪 Graal 编译器的执行过程,我们会发现它在一开始,就把字节码翻译成了一种新的 IR,这个 IR 是用图的结构来表示的。那这个图长什么样子呢?非常幸运的是,我们可以用工具来直观地看到它的结构。
你可以从 Oracle 的网站上,下载一个 idealgraphvisualizer 的工具。下载之后,解压缩,并运行它:
export PATH="/<上级目录>/idealgraphvisualizer/bin:$PATH"
idealgraphvisualizer &
这时,程序会启动一个图形界面,并在 4445 端口上等待 GraalVM 发送数据过来。
接着,还是运行 Foo 示例程序,不过这次你要增加一个参数“-Dgraal.Dump”,这会让 GraalVM 输出编译过程的一些中间结果。并且在这个示例程序当中,我还增加了一个“-Xcomp”参数,它能让 JIT 编译器在第一次使用某个方法的时候,就去做编译工作。
mx vm \
-XX:+UnlockExperimentalVMOptions \
-XX:+EnableJVMCI \
-XX:+UseJVMCICompiler \
-XX:-TieredCompilation \
-XX:CompileOnly=Foo \
-Dgraal.Dump \
-Xcomp \
Foo
GraalVM 会在终端输出“Connected to the IGV on 127.0.0.1:4445”,这表明它连接上了 idealgraphvisualizer。接着,在即时编译之后,idealgraphvisualizer 就接收到了编译过程中生成的图,你可以点击显示它。
这里我展示了其中两个阶段的图,一个是刚解析完字节码之后(After parsing),一个是在处理完中间层之后(After mid tier)。

图 1:After parsing

图 2:After mid tier
Graal IR 其实受到了“程序依赖图”的影响。我们在第 6 讲中提到过程序依赖图(PDG),它是用图来表示程序中的数据依赖和控制依赖。并且你也知道了,这种 IR 还有一个别名,叫做节点之海(Sea of Nodes)。因为当程序稍微复杂一点以后,图里的节点就会变得非常多,我们用肉眼很难看得清。
基于 Sea of Nodes 的 IR 呢,算是后起之秀。在 HotSpot 的编译器中,就采用了这种 IR,而且现在 Java 的 Graal 编译器和 JavaScript 的 V8 编译器中的 IR 的设计,都是基于了 Sea of Nodes 结构,所以我们必须重视它。
这也不禁让我们感到好奇了:Sea of Nodes 到底强在哪里?
我们都知道,数据结构的设计对于算法来说至关重要。IR 的数据结构,会影响到算法的编写方式。好的 IR 的设计,会让优化算法的编写和维护都更加容易。
而 Sea of Nodes 最大的优点,就是能够用一个数据结构同时反映控制流和数据流,并且尽量减少它们之间的互相依赖。
怎么理解这个优点呢?在传统的编译器里,控制流和数据流是分开的。控制流是用控制流图(Control-flow Graph,CFG)来表示的,比如 GNU 的编译器、LLVM,都是基于控制流图的。而 IR 本身,则侧重于表达数据流。
以 LLVM 为例,它采用了 SSA 格式的 IR,这种 IR 可以很好地体现值的定义和使用关系,从而很好地刻画了数据流。
而问题在于,采用这种比较传统的方式,控制流和数据流会耦合得比较紧,因为 IR 指令必须归属于某个基本块。
举个例子来说明一下吧。在下面的示例程序中,“int b = a*2;”这个语句,会被放到循环体的基本块中。
int foo(int a){
int sum = 0;
for(int i = 0; i< 10; i++){
int b = a*2; //这一句可以提到外面
sum += b;
}
}
可是,从数据流的角度看,变量 b 只依赖于 a。所以这个语句没必要放在循环体内,而是可以提到外面。在传统的编译器中,这一步是要分析出循环无关的变量,然后再把这条语句提出去。而如果采用 Sea of Nodes 的数据结构,变量 b 一开始根本没有归属到特定的基本块,所以也就没有必要专门去做代码的移动了。
另外,我们之前讲本地优化和全局优化的时候,也提到过,它们的区别就是,在整个函数范围内,优化的范围是在基本块内还是会跨基本块。而 Sea of Nodes 没有过于受到基本块的束缚,因此也就更容易做全局优化了。
好,那在概要地理解了 Graal IR 的数据结构之后,接下来,我们就具体了解一下 Graal IR,包括认识一下数据流与控制流的特点,了解两种不同的节点:浮动节点和固定节点,以及认识一种特殊的节点:FrameState。
数据流和控制流
我们已经知道,Graal IR 整合了两种图结构:数据流图和控制流图。
首先,我们来看看它的数据流。
在下图中,蓝色的边代表的是数据流,也就是数据之间的依赖关系。参数 1(“P(0)”节点)和参数 2(“P(1)”节点)的值流入到 + 号节点,再流入到 Return 节点。

图 3:Foo.add() 的数据流
在 Graal IR 的设计中,Add 节点有两个输入,分别是 x 和 y,这两个输入是 AddNode 的两个属性。注意,这个图中的箭头方向代表的是数据依赖关系,也就是 Add 节点保持着对它的两个输入节点的引用,这其实跟 AST 是一致的。而数据流向,则是反过来的,从 x 和 y 流向 Add 节点。
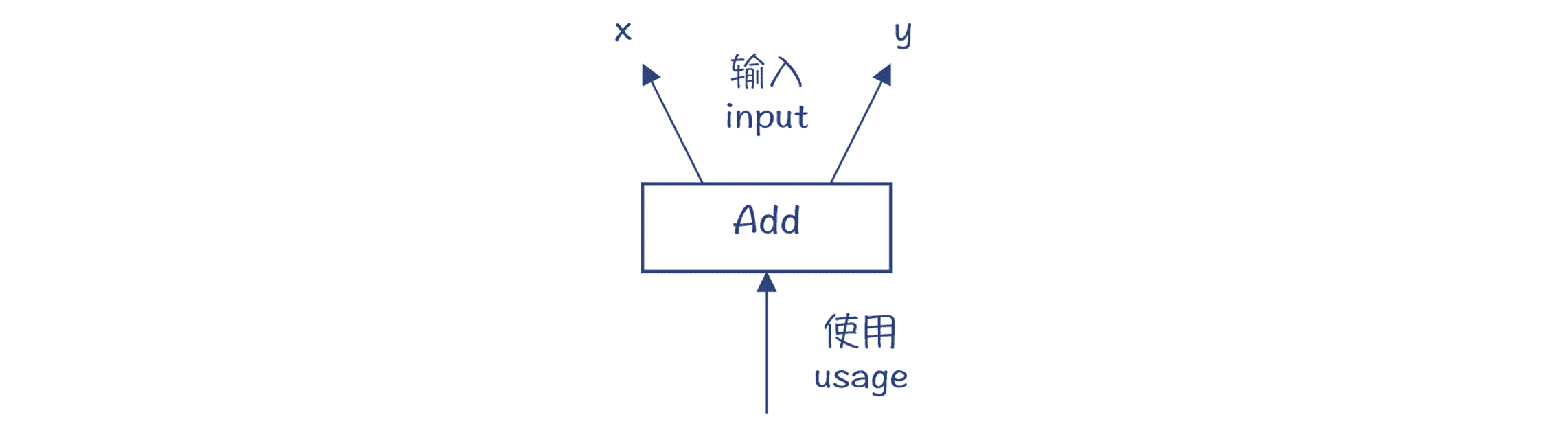
图 4:Add 节点的数据依赖关系
查看 AddNode 的设计,你会发现其父类中有两个成员变量,x 和 y。它们用 @input 做了注解,这就意味着,这两个成员变量代表的是数据流图中的两条边。

图 5:Add 节点及其各级父节点
另外,Graal IR 的数据流图是符合 SSA 格式的。也就是说,每个节点代表了 SSA 中的一个值,它只被定义一次,也就相当于 SSA 中的每个变量只被赋值一次。
我们再来看看控制流。
下图中,红色的边代表的是控制流,控制流图代表的是程序执行方向的改变。进入或退出一个函数、条件分支语句、循环语句等,都会导致程序的执行从一个地方跳到另一个地方。

图 6:Foo.add() 的控制流
数据流加上控制流,就能完整表达程序的含义,它等价于字节码,也等价于更早期的 AST。你可以从 Start 节点,沿着控制流遍历这个图。当到达 Return 节点之前,Return 所依赖的数据(x+y)也需要计算出来。
add() 方法的控制流很简单,只有 Start 和 Return 两个节点。我们做一个稍微复杂一点的例子,在 Foo.add2() 示例程序中,调用两个函数 getX() 和 getY(),分别获取 x 和 y 成员变量。
public int add2(){
return getX() + getY();
}
对应的 Graal 图如下。它增加了两个节点,分别是调用方法 getX 和 getY,这就导致了控制流发生变化。

图 7:Foo.add2() 对应的 IR
注意:对于这个例子,在使用 GraalVM 时,要使用 -XX:-Inline 选项,避免编译器做内联优化,否则 Foo.getX() 和 Foo.getY() 会被内联。我们在下一讲中就会探讨内联优化。
除了调用其他函数,if 语句、循环语句等,也会导致控制流的变化。我们看看这个例子:
public int doif(int x, int y){
int z;
if (x < 2)
z=x+y;
else
z=x*y;
return z;
}
它对应的 Graal 图如下,if 语句会让控制流产生分支,分别对应 if 块和 else 块,最后在 Merge 节点合并起来。

图 8:doif() 方法对应的 IR
IfNode 作为一种控制流节点,它保存着对下级节点的引用,并用 @Successor 注解来标注。这意味着 trueSuccessor 和 falseSuccessor 两个成员变量,代表着控制流中的两条边。当然,你也会注意到,If 节点有一个数据流的输入,这就是 If 的判断条件。IR 会基于这个判断条件,来决定控制流的走向。

图 9:IfNode 及其各级父节点
跟控制流类似,数据流也产生了两个分支,分别是x+y和x*y。最后用一个 Phi 节点合并到一起。
Phi 节点是 SSA 的一个特性。在 doif 示例程序中,z 可能有两个取值。如果控制流走的是 if 块,那么z=x+y;而如果走的是 else 块,则z=x*y。Phi 节点就起到这个作用,它根据控制流来选择值。
总结一下:控制流图表达的是控制的流转,而数据流图代表的是数据之间的依赖关系。二者双剑合璧,代表了源程序完整的语义。
接下来,我再给你介绍一下浮动节点和固定节点的概念。
浮动节点和固定节点
注意,在 Graal IR,数据流与控制流是相对独立的。你看看前面的 doif 示例程序,会发现x+y和x*y的计算,与 if 语句的控制流没有直接关系。所以,你其实可以把这两个语句挪到 if 语句外面去执行,也不影响程序运行的结果(要引入两个临时变量 z1 和 z2,分别代表 z 的两个取值)。
对于这些在执行时间上具有灵活性的节点,我们说它们是浮动的(Floating)。你在 AddNode 的继承层次中,可以看到一个父类:FloatingNode,这说明这个节点是浮动的。它可以在最后生成机器码(或 LIR)的环节,再去确定到底归属哪个基本块。
除了浮动节点以外,还有一些节点是固定在控制流中的,前后顺序不能乱,这些节点叫做固定节点。除了那些流程控制类的节点(如 IfNode)以外,还有一些节点是固定节点,比如内存访问的节点。当你访问一个对象的属性时,就需要访问内存。
内存是个共享资源,同一个内存地址(比如对象的属性),可以被多次读写。也就是说,内存位置不是 SSA 中的值,所以也不受单赋值的约束。
对同一个内存地址的读写操作,顺序是不能乱的。比如下面代码中,第二行和第三行的顺序是不能变的,它们被固定在了控制流中。
x := 10
store x to 地址 a
y := load 地址 a
z := y + 10
不过,在运行某些优化算法的时候,某些固定节点会被转化成浮动节点,从而提供了更大的代码优化空间。我们在下一讲的“内联和逃逸分析”中,会见到这样的例子。
FrameState 节点
在看 Graal IR 的时候,你经常会遇到一个绿色的节点插在图中。为避免你产生困惑,接下来我就专门给你解释一下这个节点,我们一起来认识一下它。
在 Foo.add() 新生成的 IR 中,如果你不勾选“Remove State”选项,就会显示出一个绿色的节点。这个节点就是 FrameState 节点。
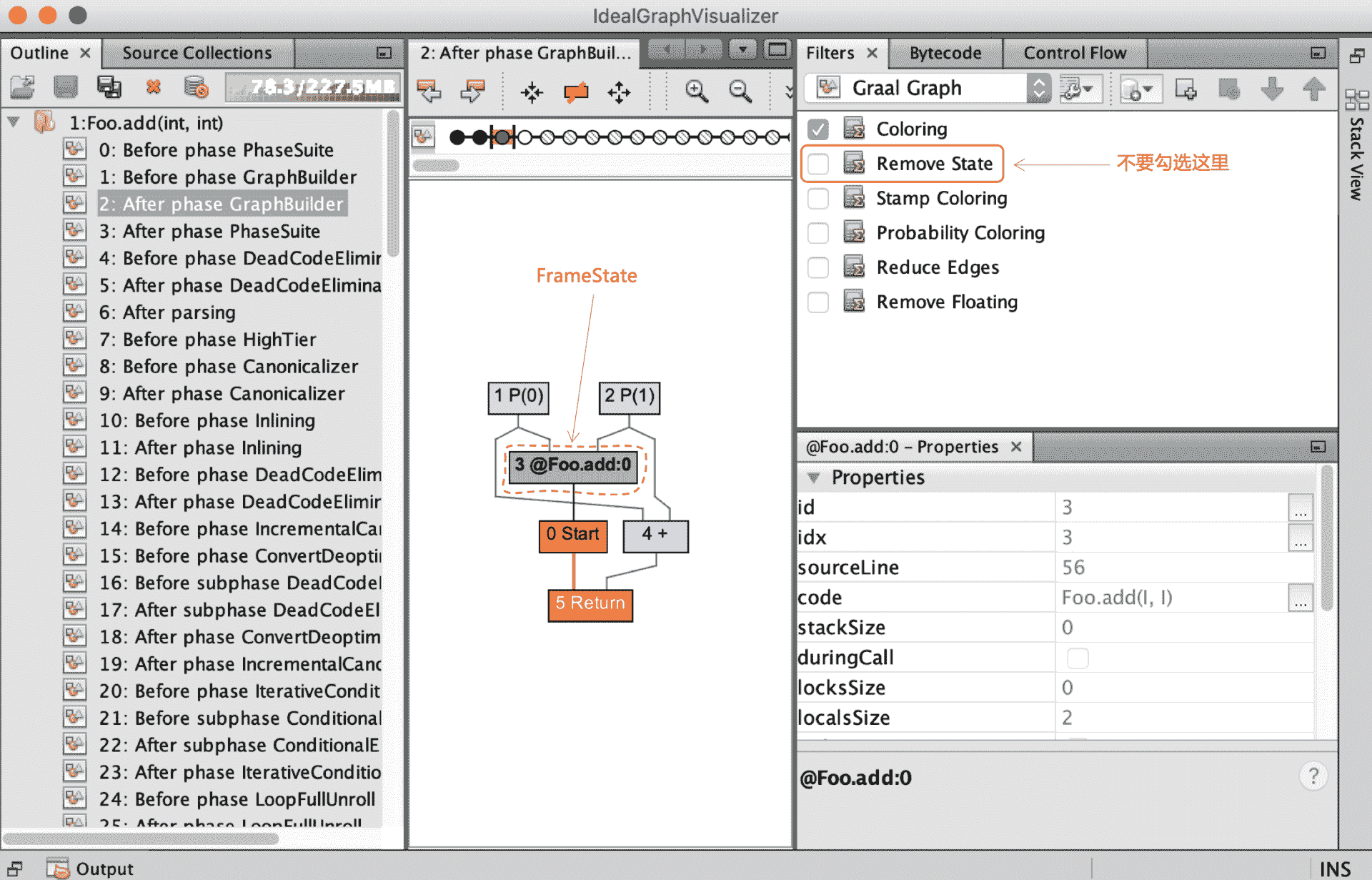
图 10:Foo.add() 中的 FrameState 节点
FrameState 比较特殊。它保存了栈帧的状态,而且这里我指的是 Java 字节码解释器的栈帧的状态,包括了本地变量和操作数栈里的值。
为什么要保存栈帧的状态呢?
**第一个用途,是用于逆优化。**上一讲我们说过,编译器有时候会基于推测做一些激进的优化,比如忽略掉某些分支。但如果推测依据的前提错了,那么就要做逆优化,重新回到解释器去执行。而 FrameState 的作用就是在代码中一些叫做安全点的地方,记录下栈帧的状态,便于逆优化以后,在解释器里去接着执行程序。
**第二个用途,是用于 debug。**编译器会用 FrameState,来记录程序执行的一些中间状态值,以方便程序的调试。
对于 Foo.add() 方法的 IR,通过后面的一些优化处理,你会发现 Foo.add() 并不需要逆优化,那么 FrameState 节点就会被去掉。否则,FrameState 就会转化成一个逆优化节点,生成与逆优化有关的代码。
如果你并不关心逆优化,那你在平常看 IR 的过程中,可以勾选“Remove State”选项,不用关注 FrameState 节点就行了。
好了,我们已经大致了解了 Graal IR。进一步,编译器要基于 IR 做各种处理和优化。
对 Graal IR 的处理和优化
通过上一讲,我们已经知道在编译过程中要对图进行很多遍的处理。还是以 Foo.add() 示例程序为例,在运行 GraalVM 的时候,我们加上“-Dgraal.Dump=:5”选项,程序就会详细地 dump 出所做的处理步骤,你可以在 idealgraphvisualizer 中看到这些处理环节,点击每个环节可以看到相对应的 IR 图。

图 11:对 Foo.add() 所做的处理
在这些处理阶段的名称中,你会看到我们在第 7 讲中提到的一些代码优化算法的名称(如死代码删除)。有了前面课程的铺垫,你现在看它们应该就消除了一些陌生感。
另外,你会发现,在这些处理阶段中,有一个 Canonicalizer 的阶段出现了好几次,并且你可能对这个词也比较陌生,所以下面我们不妨来看看,这个阶段都做了些什么。
规范化(Canonicalizer)
Canonicalize 的意思是规范化。如果某段程序有多种写法,那么编译器会处理成一种统一的、标准的写法。
比如,对于下面这个简单的函数,它是把 a 乘以 2。在 CanonicalizerPhase 运行之后,乘法运算被替换成了移位运算,也就是a<<1。它的效果与乘以 2 是相同的,但运行效率更高。
public int doDouble(int a){
return 2*a;
}

图 12:未做规范化优化之前,是乘法运算

图 13:做完规范化优化之后,变成移位运算
你还可以试一下对某个变量取两次负号的操作。在规范化阶段以后,两个负号就会被去掉,直接返回 a。
public int negneg(int a){
return -(-a);
}
规范化需要的操作,都是对本节点进行修改和替换,一般都不太复杂。某节点如果实现了 Canonicalizable 接口,在 CanonicalizerPhase 就会对它做规范化。
在规范化阶段实现的优化算法包括:常数折叠(Constant Folding)、强度折减(Strength reduction)、全局值编号(Global Value Numbering,GVN),等等。它们的原理,我在第 7 讲都介绍过,这里就不赘述了。
课程小结
这一讲,我给你介绍了 Graal 的 IR:它整合了控制流图与数据流图,符合 SSA 格式,有利于优化算法的编写和维护。
我还带你了解了对 IR 的一个优化处理过程:规范化。规范化所需要的操作一般并不复杂,它都是对本节点进行修改和替换。在下一讲中,我会带你分析另外两个重要的算法,内联和逃逸分析。
另外,Graal 的 IR 格式是声明式的(Declarative),它通过描述一个节点及其之间的关系来反映源代码的语义。而我们之前见到的类似三地址代码那样的格式,是命令式的(Imperative),它的风格是通过命令直接告诉计算机,来做一个个的动作。
声明式和命令式是编程的两种风格,在 Graal 编译器里,我们可以看到声明式的 IR 会更加简洁,对概念的表达也更加清晰。我们在后面介绍 MySQL 编译器的实现机制当中,在讲 DSL 的时候,还会再回到这两个概念,到时你还会有更加深刻的认识。
本讲的思维导图我也放在了这里,供你参考:

一课一思
了解了 Graal IR 的特点以后,通过对比我们在第 7 讲中学过的优化算法,你觉得哪些优化算法在 Graal IR 上实现起来会更方便?为什么?欢迎在留言区分享你的看法。
如果你觉得有收获,也欢迎你把今天的内容分享给更多的朋友。
参考资料
基于图的 IR,有三篇论文必须提到:
- 程序依赖图:J. Ferrante, K. J. Ottenstein, and J. D. Warren. The program dependence graph and its use in optimization. July 1987。有关程序依赖图的概念在 1987 年就提出来了。
- Click 的论文:A Simple Graph-Based Intermediate Representation。这篇文章比较易读,属于必读文献。Click 还发表了一些论文,讲述了基于图的 IR 上的优化算法。
- 介绍 Graal IR 的论文:Graal IR: An Extensible Declarative Intermediate Representation。这篇论文也很易读,建议你一定要读一下。
文章作者
上次更新 2025-01-03