14__如何使用片元着色器进行几何造型?
文章目录
你好,我是月影。
在 WebGL 中,片元着色器有着非常强大的能力,它能够并行处理图片上的全部像素,让数以百万计的运算同时完成。但也正因为它是并行计算的,所以它和常规代码顺序执行或者串行执行过程并不一样。因此,在使用片元着色器实现某些功能的时候,我们要采用与常规的 JavaScript 代码不一样的思路。
到底哪里不一样呢?今天,我就通过颜色控制,以及线段、曲线、简单几何图形等的绘制,来讲讲片元着色器是怎么进行几何造型的,从而加深你对片元着色器绘图原理的理解。
首先,我们来说比较简单的颜色控制。
如何用片元着色器控制局部颜色?
我们知道,片元着色器能够用来控制像素颜色,最简单的就是把图片绘制为纯色。比如,通过下面的代码,我们就把一张图片绘制为了纯黑色。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
gl_FragColor = vec4(0, 0, 0, 1);
}
如果想让一张图片呈现不同的颜色,我们还可以根据纹理坐标值来绘制,比如,通过下面的代码,我们就可以让某个图案的颜色,从左到右由黑向白过渡。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
gl_FragColor.rgb = vec3(vUv.x);
gl_FragColor.a = 1.0;
}
不过,这种颜色过渡还比较单一,这里我们还可以改变一下渲染方式让图形呈现的效果更复杂。比如说,我们可以使用乘法创造一个 10*10 的方格,让每个格子左上角是绿色,右下角是红色,中间是过渡色。代码和显示的效果如下所示:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
vec2 st = vUv * 10.0;
gl_FragColor.rgb = vec3(fract(st), 0.0);
gl_FragColor.a = 1.0;
}
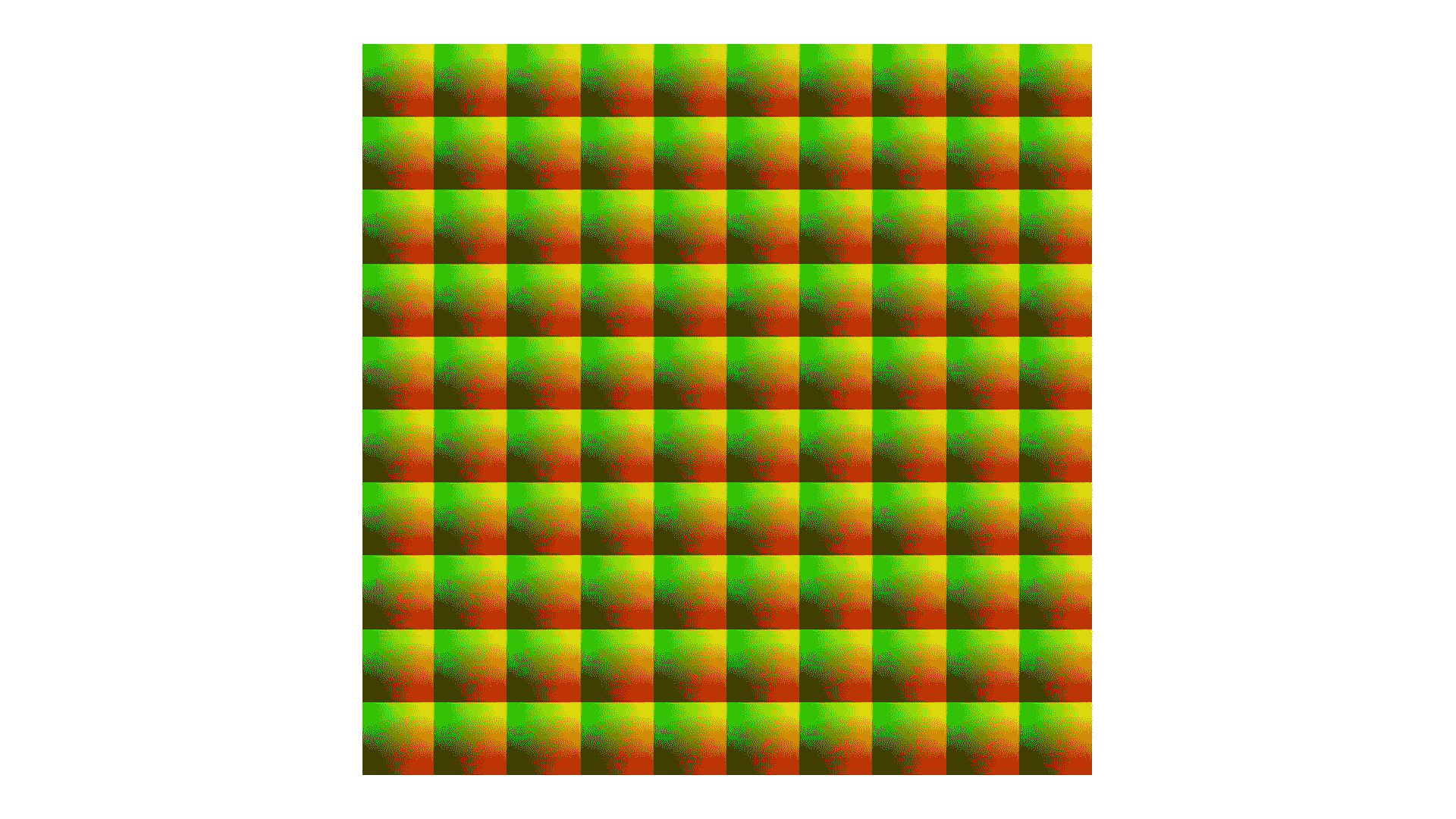
不仅如此,我们还可以在上图的基础上继续做调整。我们可以通过 idx = floor(st) 获取网格的索引,判断网格索引除以 2 的余数(奇偶性),根据它来决定是否翻转网格内的 x、y 坐标。这样操作后的代码和图案如下所示:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
vec2 st = vUv * 10.0;
vec2 idx = floor(st);
vec2 grid = fract(st);
vec2 t = mod(idx, 2.0);
if(t.x == 1.0) {
grid.x = 1.0 - grid.x;
}
if(t.y == 1.0) {
grid.y = 1.0 - grid.y;
}
gl_FragColor.rgb = vec3(grid, 0.0);
gl_FragColor.a = 1.0;
}

事实上,再改用不同的方式,我们还可以生成更多有趣的图案。不过,这里我们就不继续了,因为上面这些做法有点像是灵机一动的小技巧。实际上,我们缺少的并不是小技巧,而是一套统一的方法论。我们希望能够利用它,在着色器里精确地绘制出我们想要的几何图形。
如何用片元着色器绘制圆、线段和几何图形
那接下来,我们就通过几个例子,把片元着色器精确绘图的方法论给总结出来。
1. 绘制圆
首先,我们从最简单的几何图形,也就是圆开始,来说说片元着色器的绘图过程。
一般来说,我们画圆的时候是根据点坐标到圆心的距离来生成颜色的。在片元着色器中,我们可以用 distance 函数求一下 vUv 和画布中点 vec2(0.5) 的距离,然后根据这个值设置颜色。代码如下:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
float d = distance(vUv, vec2(0.5));
gl_FragColor.rgb = d * vec3(1.0);
gl_FragColor.a = 1.0;
}
通过这样的方法,我们最终绘制出了一个模糊的圆,效果如下:

为什么这个圆是模糊的呢?这是因为越靠近圆心,距离 d 的值越小,gl_FragColor.rgb = d * vec3(1.0); 的颜色值也就越接近于黑色。
那如果我们要实现一个更清晰的圆应该怎么做呢?这个时候,你别忘了还有 step 函数。我们用 step 函数基于 0.2 做阶梯,就能得到一个半径为 0.2 的圆。实现代码和最终效果如下:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
float d = distance(vUv, vec2(0.5));
gl_FragColor.rgb = step(d, 0.2) * vec3(1.0);
gl_FragColor.a = 1.0;
}

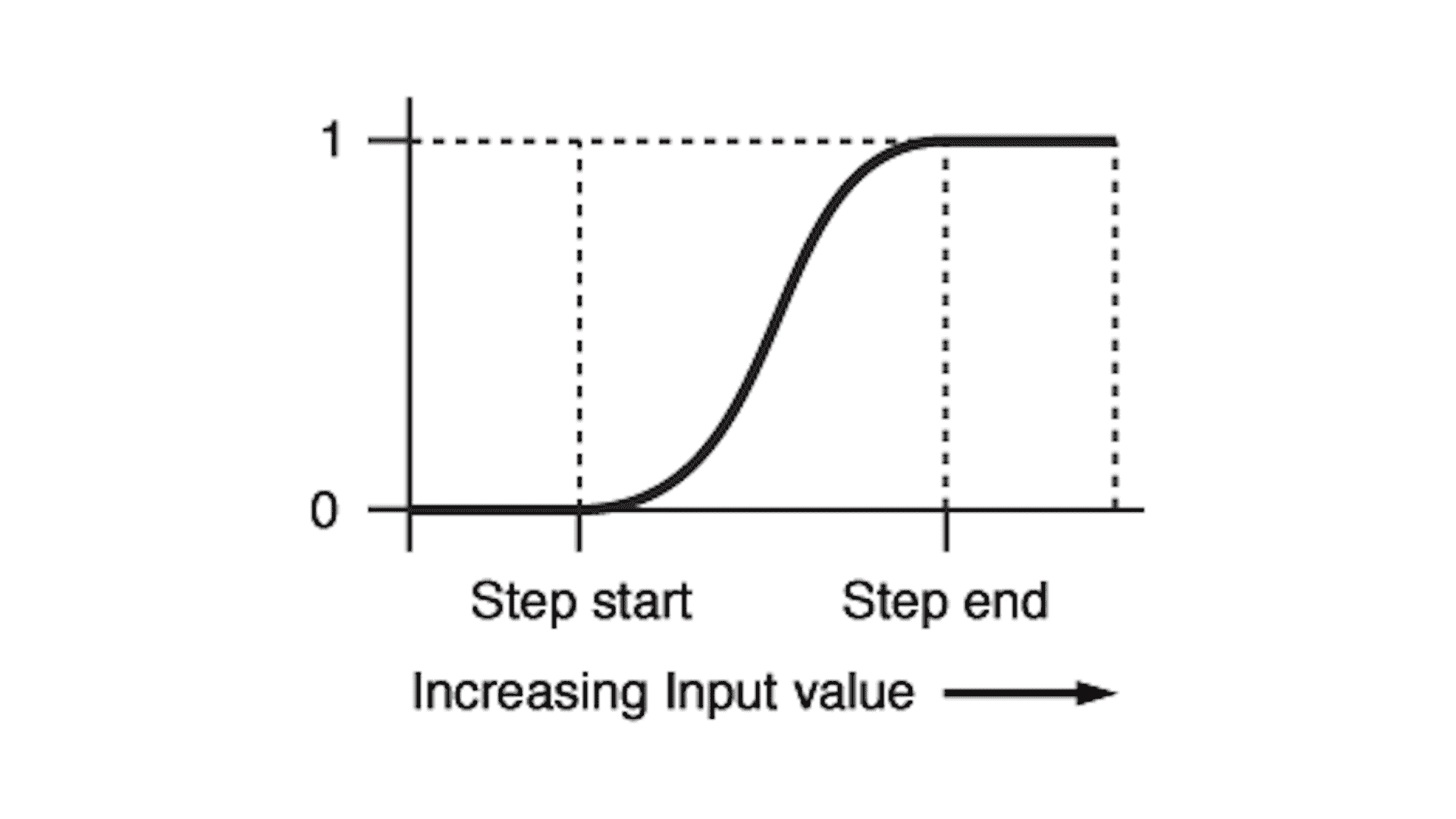
不过,你会发现我们得到的这个圆的边缘很不光滑。这是因为浮点数计算的精度导致的锯齿现象。为了解决这个问题,我们用 smoothstep 代替 step。

为什么 smoothstep 代替 step 就可以得到比较光滑的圆呢?这是因为 smoothstep 和 step 类似,都是阶梯函数。但是,与 step 的值是直接跳跃的不同,smoothstep 在 step-start 和 step-end 之间有一个平滑过渡的区间。因此,用 smoothstep 绘制的圆,边缘就会有一圈颜色过渡,就能从视觉上消除锯齿。
片元着色器绘制的圆,在构建图像的粒子效果中比较常用。比如,我们可以用它来实现图片的渐显渐隐效果。下面是片元着色器中代码,以及我们最终能够实现的效果图。
#ifdef GL_ES
precision highp float;
#endif
uniform sampler2D tMap;
uniform vec2 uResolution;
uniform float uTime;
varying vec2 vUv;
float random (vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))*
43758.5453123);
}
void main() {
vec2 uv = vUv;
uv.y *= uResolution.y / uResolution.x;
vec2 st = uv * 100.0;
float d = distance(fract(st), vec2(0.5));
float p = uTime + random(floor(st));
float shading = 0.5 + 0.5 * sin(p);
d = smoothstep(d, d + 0.01, 1.0 * shading);
vec4 color = texture2D(tMap, vUv);
gl_FragColor.rgb = color.rgb * clamp(0.5, 1.3, d + 1.0 * shading);
gl_FragColor.a = color.a;
}

2. 绘制线
利用片元着色器绘制圆的思路,就是根据点到圆心的距离来设置颜色。实际上,我们也可以用同样的原理来绘制线,只不过需要把点到点的距离换成点到直线(向量)的距离。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
vec3 line = vec3(1, 1, 0);
float d = abs(cross(vec3(vUv,0), normalize(line)).z);
gl_FragColor.rgb = (1.0 - smoothstep(0.0, 0.01, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
比如,我们利用上面的代码,就能在画布上画出一条斜线。

如果你还不能一眼看出上面的代码为什么能画出一条直线,说明你对于图形学的向量计算思维还没有完全适应。不过别着急,随着我们练习的增多,你会逐渐适应的。下面,我来解释一下这段代码。
这里,我们用一个三维向量 line 来定义一条直线。因为我们要绘制的是 2D 图形,所以 z 保持 0 就行,而 x 和 y 用来决定方向。
然后呢,我们求 vUv 和 line 的距离。这里我们直接用向量叉乘的性质就能求得。因为两个二维向量叉积的 z 轴分量的大小,就是这两个向量组成的平行四边形的面积,那当我们把 line 的向量归一化之后,这个值就是 vUv 到直线的距离 d 了。因为这个 d 带符号,所以我们还需要取它的绝对值。
最后,我们用这个 d 结合前面使用过的 smoothstep 来控制像素颜色,就能得到一条直线了。
3. 用鼠标控制直线
画出直线之后,我们改变 line 还可以得到不同的直线。比如,在着色器代码中,我们再添加一个 uniform 变量 uMouse,就可以根据鼠标位置来控制直线方向。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
uniform vec2 uMouse;
void main() {
vec3 line = vec3(uMouse, 0); // 用向量表示所在直线
float d = abs(cross(vec3(vUv,0), normalize(line)).z); // 叉乘表示平行四边形面积,底边为 1,得到距离
gl_FragColor.rgb = (1.0 - smoothstep(0.0, 0.01, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
对应地,我们需要在 JavaScript 中将 uMouse 通过 uniforms 传入,代码如下:
const canvas = document.querySelector(‘canvas’);
const renderer = new GlRenderer(canvas);
const program = renderer.compileSync(fragment, vertex);
renderer.useProgram(program);
renderer.uniforms.uMouse = [-1, -1];
canvas.addEventListener(‘mousemove’, (e) => {
const {x, y, width, height} = e.target.getBoundingClientRect();
renderer.uniforms.uMouse = [
(e.x - x) / width,
1.0 - (e.y - y) / height,
];
});
renderer.setMeshData([{
positions: [
[-1, -1],
[-1, 1],
[1, 1],
[1, -1],
],
attributes: {
uv: [
[0, 0],
[0, 1],
[1, 1],
[1, 0],
],
},
cells: [[0, 1, 2], [2, 0, 3]],
}]);
renderer.render();

在上面的例子中,我们的直线是经过原点的。那如果我们想让直线经过任意的定点该怎么办?我们可以加一个 uniform 变量 uOrigin,来表示直线经过的固定点。代码如下:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
uniform vec2 uMouse;
uniform vec2 uOrigin;
void main() {
vec3 line = vec3(uMouse - uOrigin, 0); // 用向量表示所在直线
float d = abs(cross(vec3(vUv - uOrigin, 0), normalize(line)).z); // 叉乘表示平行四边形面积,底边为 1,得到距离
gl_FragColor.rgb = (1.0 - smoothstep(0.0, 0.01, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
延续这个绘制直线的思路,我们很容易就能知道该如何绘制线段了。绘制线段与绘制直线的方法几乎一样,只不过,我们要将计算点到直线的距离修改为计算点到线段的距离。
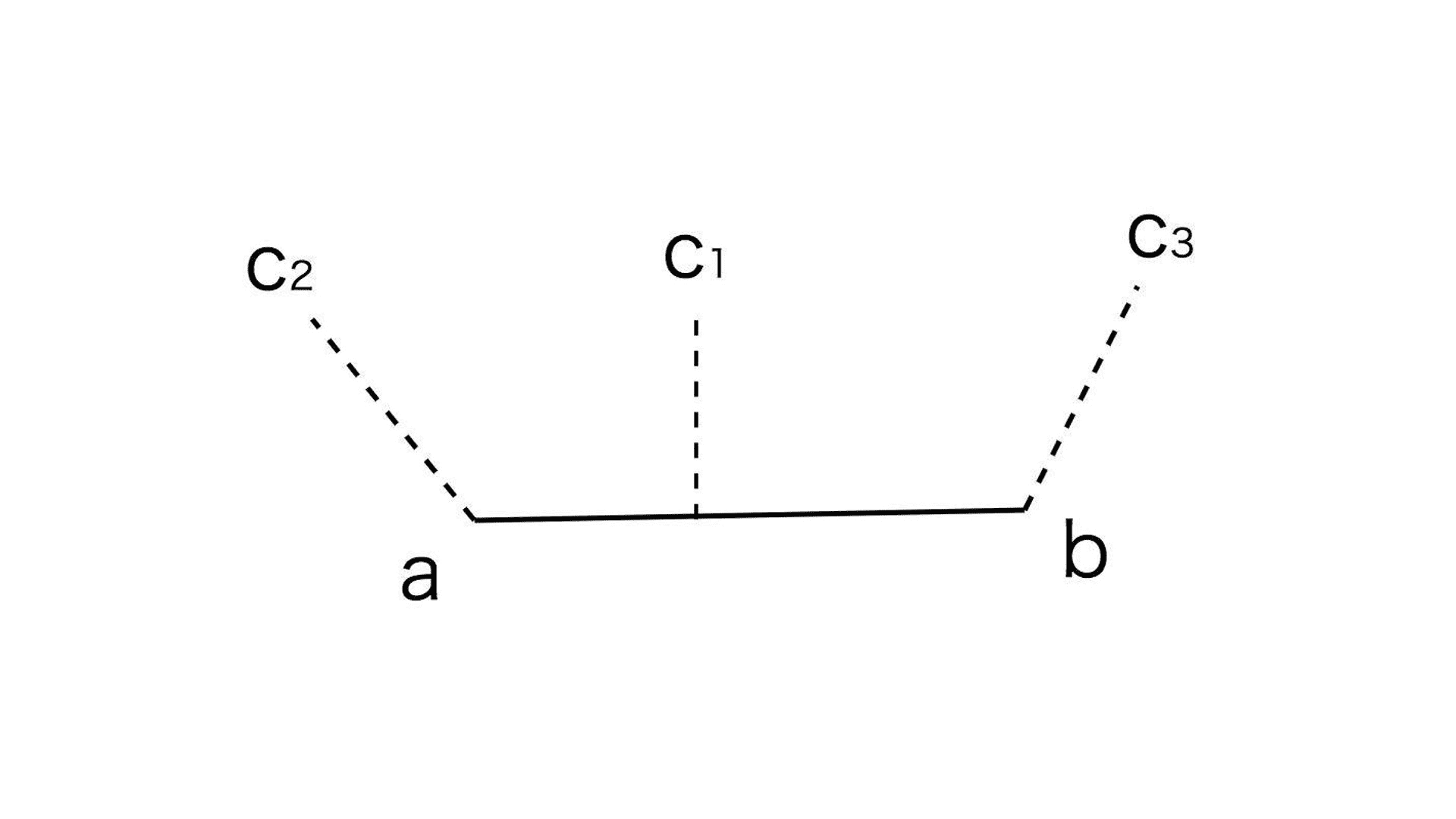
但是因为点和线段之间有两种关系,一种是点在线段上,另一种是在线段之外。所以我们在求点到线段的距离 d 的时候,要分两种情况讨论:当点到线段的投影位于线段两个端点中间的时候,它就等于点到直线的距离;当点到线段的投影在两个端点之外的时候,它就等于这个点到最近一个端点的距离。
这么说还是比较抽象,我画了一个示意图。你会看到,C1到线段 ab 的距离就等于它到线段所在直线的距离,C2到线段 ab 的距离是它到 a 点的距离,C3到线段的距离是它到 b 点的距离。那么如何判断究竟是 C1、C2、C3中的哪一种情况呢?答案是通过 C1到线段 ab 的投影来判断。
所以,我们在原本片元着色器代码的基础上,抽象出一个 seg_distance 函数,用来返回点到线段的距离。修改后的代码如下:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
uniform vec2 uMouse;
uniform vec2 uOrigin;
float seg_distance(in vec2 st, in vec2 a, in vec2 b) {
vec3 ab = vec3(b - a, 0);
vec3 p = vec3(st - a, 0);
float l = length(ab);
float d = abs(cross(p, normalize(ab)).z);
float proj = dot(p, ab) / l;
if(proj >= 0.0 && proj <= l) return d;
return min(distance(st, a), distance(st, b));
}
void main() {
float d = seg_distance(vUv, uOrigin, uMouse);
gl_FragColor.rgb = (1.0 - smoothstep(0.0, 0.01, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
这么修改之后,如果我们将 uOrigin 设为 vec2(0.5, 0.5),就会得到如下效果:

4. 绘制三角形
你可能已经发现了,不管是画圆还是画线,我们使用的原理都是求点到点或者是点到线段距离。实际上,这个原理还可以扩展应用到封闭平面图形的绘制上。那我们就以三角形为例,来说说片元着色器的绘制结合图形的方法。
首先,我们要判断点是否在三角形内部。我们知道,点到三角形三条边的距离有三个,只要这三个距离的符号都相同,我们就能确定点在三角形内。
然后,我们建立三角形的距离模型。我们规定它的内部距离为负,外部距离为正,并且都选点到三条边的最小距离。代码如下:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
float line_distance(in vec2 st, in vec2 a, in vec2 b) {
vec3 ab = vec3(b - a, 0);
vec3 p = vec3(st - a, 0);
float l = length(ab);
return cross(p, normalize(ab)).z;
}
float seg_distance(in vec2 st, in vec2 a, in vec2 b) {
vec3 ab = vec3(b - a, 0);
vec3 p = vec3(st - a, 0);
float l = length(ab);
float d = abs(cross(p, normalize(ab)).z);
float proj = dot(p, ab) / l;
if(proj >= 0.0 && proj <= l) return d;
return min(distance(st, a), distance(st, b));
}
float triangle_distance(in vec2 st, in vec2 a, in vec2 b, in vec2 c) {
float d1 = line_distance(st, a, b);
float d2 = line_distance(st, b, c);
float d3 = line_distance(st, c, a);
if(d1 >= 0.0 && d2 >= 0.0 && d3 >= 0.0 || d1 <= 0.0 && d2 <= 0.0 && d3 <= 0.0) {
return -min(abs(d1), min(abs(d2), abs(d3))); // 内部距离为负
}
return min(seg_distance(st, a, b), min(seg_distance(st, b, c), seg_distance(st, c, a))); // 外部为正
}
void main() {
float d = triangle_distance(vUv, vec2(0.3), vec2(0.5, 0.7), vec2(0.7, 0.3));
gl_FragColor.rgb = (1.0 - smoothstep(0.0, 0.01, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
这样,我们就绘制出了一个白色的三角形。

实际上,三角形的这种画法还可以推广到任意凸多边形。比如,矩形和正多边形就可以使用同样的方式来绘制。
片元着色器绘图方法论:符号距离场渲染
现在,你应该知道这些基本的线段、圆和几何图形该怎么绘制了。那我们能不能从中总结出一套统一的方法论呢?我们发现,前面绘制的图形虽然各不相同,但是它们的绘制步骤都可以总结为以下两步。
第一步:定义距离。这里的距离,是一个人为定义的概念。在画圆的时候,它指的是点到圆心的距离;在画直线和线段的时候,它是指点到直线或某条线段的距离;在画几何图形的时候,它是指点到几何图形边的距离。
第二步:根据距离着色。首先是用 smoothstep 方法,选择某个范围的距离值,比如在画直线的时候,我们设置 smoothstep(0.0, 0.01, d),就表示选取距离为 0.0 到 0.01 的值。然后对这个范围着色,我们就可以将图形的边界绘制出来了。
延续这个思路,我们还可以选择距离在 0.0~0.01 范围以外的点。下面,我们做一个小实验。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
vec3 line = vec3(1, 1, 0);
float d = abs(cross(vec3(vUv,0), normalize(line)).z);
gl_FragColor.rgb = (smoothstep(0.195, 0.2, d) - smoothstep(0.2, 0.205, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
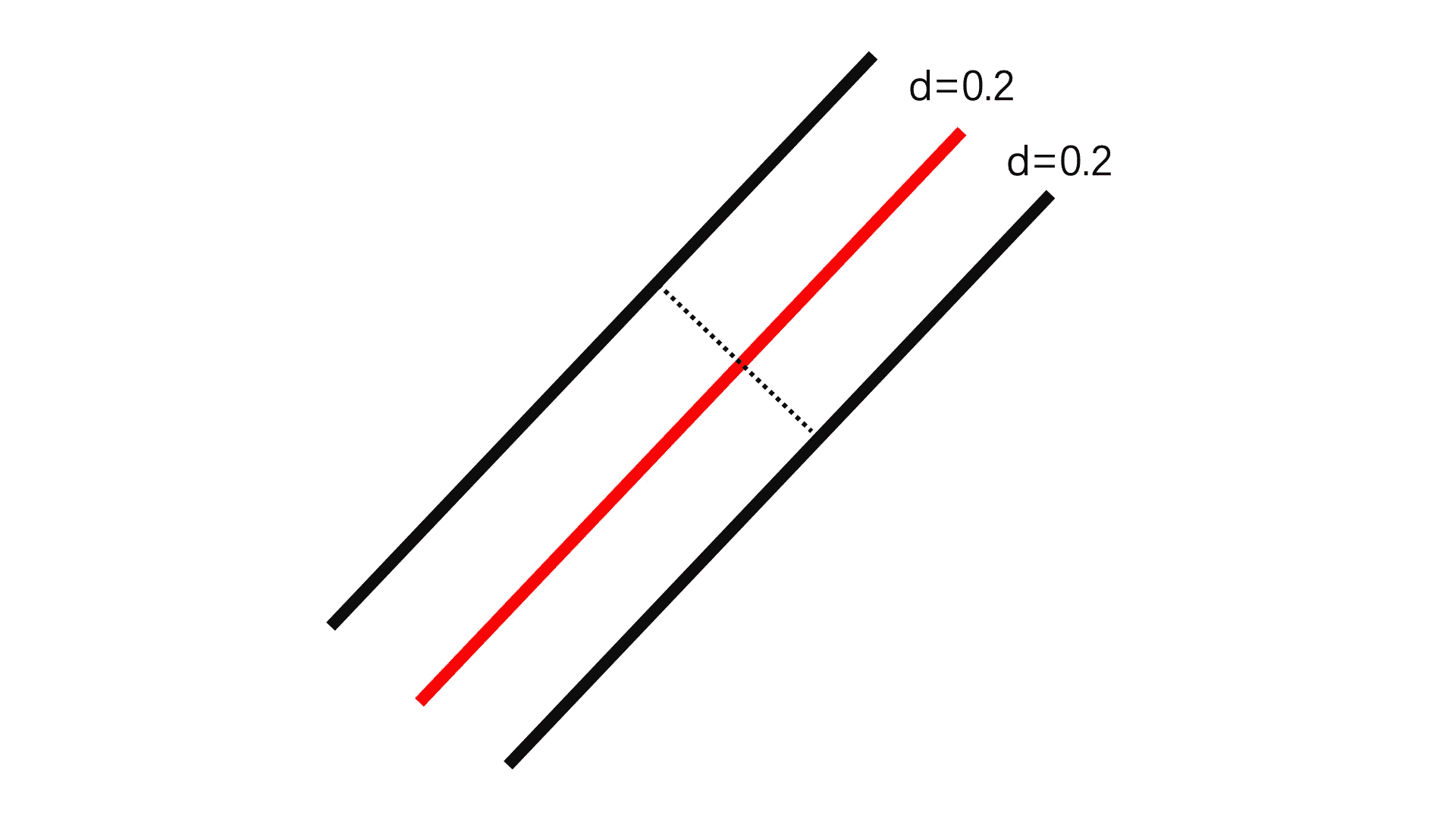
我们用之前绘制直线的代码,将 gl_FragColor.rgb = (1.0 - smoothstep(0.0, 0.01, d)) * vec3(1.0) 修改为 gl_FragColor.rgb = (smoothstep(0.195, 0.2, d) - smoothstep(0.2, 0.205, d)) * vec3(1.0),我们看到输出的结果变成对称的两条直线了。

这是为什么呢?因为我们是对距离原直线 0.2 处的点进行的着色,那实际上距离 0.2 的点有两条线,所以就能绘制出两条直线了。我把它的原理画了一个示意图,你可以看看,其中红线是原直线。
利用这个思路,再加上使用乘法和 fract 函数重复绘制的原理,我们就可以绘制多条平行线了。比如通过下面的代码,我们可以绘制出均匀的平面分割线。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
vec3 line = vec3(1, 1, 0);
float d = abs(cross(vec3(vUv,0), normalize(line)).z);
d = fract(20.0 * d);
gl_FragColor.rgb = (smoothstep(0.45, 0.5, d) - smoothstep(0.5, 0.55, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}

利用同样的办法,我们还可以绘制圆环或者三角环或者其他图形的环。因为原理相同,下面我就直接给你展示代码和效果了。
首先是绘制圆环的代码和效果:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
void main() {
float d = distance(vUv, vec2(0.5));
d = fract(20.0 * d);
gl_FragColor.rgb = (smoothstep(0.45, 0.5, d) - smoothstep(0.5, 0.55, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}

然后是绘制三角环的代码和效果:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
float line_distance(in vec2 st, in vec2 a, in vec2 b) {
vec3 ab = vec3(b - a, 0);
vec3 p = vec3(st - a, 0);
float l = length(ab);
return cross(p, normalize(ab)).z;
}
float seg_distance(in vec2 st, in vec2 a, in vec2 b) {
vec3 ab = vec3(b - a, 0);
vec3 p = vec3(st - a, 0);
float l = length(ab);
float d = abs(cross(p, normalize(ab)).z);
float proj = dot(p, ab) / l;
if(proj >= 0.0 && proj <= l) return d;
return min(distance(st, a), distance(st, b));
}
float triangle_distance(in vec2 st, in vec2 a, in vec2 b, in vec2 c) {
float d1 = line_distance(st, a, b);
float d2 = line_distance(st, b, c);
float d3 = line_distance(st, c, a);
if(d1 >= 0.0 && d2 >= 0.0 && d3 >= 0.0 || d1 <= 0.0 && d2 <= 0.0 && d3 <= 0.0) {
return -min(abs(d1), min(abs(d2), abs(d3))); // 内部距离为负
}
return min(seg_distance(st, a, b), min(seg_distance(st, b, c), seg_distance(st, c, a))); // 外部为正
}
void main() {
float d = triangle_distance(vUv, vec2(0.3), vec2(0.5, 0.7), vec2(0.7, 0.3));
d = fract(20.0 * abs(d));
gl_FragColor.rgb = (smoothstep(0.45, 0.5, d) - smoothstep(0.5, 0.55, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}

实际上,上面这种绘制图形和环的方式,在图形渲染中有一个专有的名称叫做符号距离场渲染(Signed Distance Fields Rendering)。它本质上就是利用空间中的距离分布来着色的。我们把上面的三角环代码换一种渲染方式,你就能看得更清楚一些了。代码如下:
void main() {
float d = triangle_distance(vUv, vec2(0.3), vec2(0.5, 0.7), vec2(0.7, 0.3));
d = fract(20.0 * abs(d));
gl_FragColor.rgb = vec3(d);
// gl_FragColor.rgb = (smoothstep(0.45, 0.5, d) - smoothstep(0.5, 0.55, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
我们在渲染的时候,还可以把 main 函数中原来的 smoothstep 渲染方式注释掉,直接用 vec3(d) 来渲染颜色,就会得到的如下的效果。

你能看到,这里的每一环,两两之间的距离是沿着法线方向从 0 到 1 的,所以颜色从黑色过渡到白色,这就是三角环的距离场分布。相同颜色值的环线就是距离场的等距线,我们用 step 或 smoothstep 的方式将某些等距线的颜色设置为白色,其他位置颜色设置为黑色,就绘制出之前的环线效果来了。
着色器绘制几何图形的用途
讨论到这里,你一定有些疑惑,我们学习这些片元着色器的绘图方式,究竟有什么实际用途呢?实际上它的用途还是挺广泛的,在这里我想先简单举几个实际的应用案例,你可以先感受一下。
不过,在讲具体案例之前,我还想多啰嗦几句。着色器造型是着色器的一种非常基础的使用方法,甚至可以说是图形学中着色器渲染最基础的原理,就好比代数的基础是四则运算一样,它构成了 GPU 视觉渲染的基石,我们在视觉呈现中生成的各种细节特效的方法,万变不离其宗,基本上都和着色器造型有关。
所以呢,我希望你不仅仅要了解它的用途,更要彻底弄明白它的原理和思路,尤其是非常重要的符号距离场渲染技巧,一定要理解并熟练掌握。关于着色器造型的更多、更复杂的应用场景,我们在后续的课程中还会遇到。明白了这一点,我们接着来看三个简单的案例吧。
首先,我们可以用着色器造型实现图像的剪裁。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
uniform sampler2D tMap;
uniform float uTime;
…
void main() {
vec4 color = texture2D(tMap, vUv);
vec2 uv = vUv - vec2(0.5);
vec2 a = vec2(-0.577, 0) - vec2(0.5);
vec2 b = vec2(0.5, 1.866) - vec2(0.5);
vec2 c = vec2(1.577, 0) - vec2(0.5);
float scale = min(1.0, 0.0005 * uTime);
float d = triangle_distance(uv, scale * a, scale * b, scale * c);
gl_FragColor.rgb = (1.0 - smoothstep(0.0, 0.01, d)) * color.rgb;
gl_FragColor.a = 1.0;
}
利用上面的代码,我们对图像进行三角形剪裁,可以实现的效果如下:

其次,我们可以实现对图像的动态修饰,比如类似下面这种进度条。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
uniform sampler2D tMap;
uniform float uTime;
…
void main() {
vec4 color = texture2D(tMap, vUv);
vec2 uv = vUv - vec2(0.5);
vec2 a = vec2(0, 1);
float time = 0.0005 * uTime;
vec2 b = vec2(sin(time), cos(time));
float d = 0.0;
float c0 = cross(vec3(b, 0.0), vec3(a, 0.0)).z;
float c1 = cross(vec3(uv, 0.0), vec3(a, 0.0)).z;
float c2 = cross(vec3(uv, 0.0), vec3(b, 0.0)).z;
if(c0 > 0.0 && c1 > 0.0 && c2 < 0.0) {
d = 1.0;
}
if(c0 < 0.0 && (c1 >= 0.0 || c2 <= 0.0)) {
d = 1.0;
}
gl_FragColor.rgb = color.rgb;
gl_FragColor.r *= mix(0.3, 1.0, d);
gl_FragColor.a = mix(0.9, 1.0, d);
}

第三,我们还可以在一些 3D 场景中修饰几何体,比如像这样给一个球体套一个外壳,这个例子的代码我就不贴出来了,在后续 3D 课程中我们再详细来说。

要点总结
这一节课,我们学习了使用片元着色器进行几何造型的 2 种常用方法。
首先,用片元着色器可以通过控制局部颜色来绘制图案,比如根据像素坐标来控制颜色变化,然后利用重复绘制的技巧,形成有趣的图案花纹。
其次,我们可以定义并计算像素坐标的距离,然后根据距离来填充颜色,这种方法实际上叫做符号距离场渲染,是着色器造型生成图案的基础方法。通过这种方法我们可以绘制圆、直线、线段、三角形以及其他图形。
使用着色器绘制几何图形是 WebGL 常用的方式,它有许多用途,比如可以剪裁图像、显示进度条、实现外壳纹路等等,因此在可视化中有许多使用场景。
小试牛刀
这一节课我们介绍了圆、直线、线段和三角形的基本画法,其他图形也可以用 t 方法来绘制。试着用同样的思路来绘制正方形、正六角星、椭圆吧!
欢迎在留言区和我讨论,分享你的答案和思考,也欢迎你把这节课分享给你的朋友,我们下节课再见!
源码
本节课完整代码.
文章作者
上次更新 2025-01-03