30_应用开发:北京市小客车(汽油车)摇号趋势分析
文章目录
你好,我是吴磊。
如果你也在北京生活,那小汽车摇号这件事大概率也和你息息相关。我身边很多人也一直都和我抱怨说:“小汽车摇号这件事太难了,遥遥无期,完全看不到希望,感觉还没买彩票靠谱呢”。
实不相瞒,我自己也在坚持小汽车摇号,在享受 8 倍概率的情况下,还是没能中签。因此,包括我在内的很多人都想知道,为什么摇号这么费劲?一个人平均需要参与多少次摇号才会中签?中签率的变化趋势真的和官方宣布的一致吗?倍率这玩意儿,真的能提高中签的概率吗?
这些问题,我们都能通过开发一个北京市小汽车摇号趋势分析的应用来解答。我会用两讲的时间带你完成这个应用的开发,在这个过程中,我们可以把前面学过的原理篇、通用调优篇和 Spark SQL 调优篇的大部分知识都上手实践一遍,是不是一听就很期待呢?
话不多说,我们赶紧开始吧!
课前准备
既然是做开发,那我们就需要做一些准备工作。准备工作分为 3 部分,分别是准备数据、准备开发环境和准备运行环境。
准备数据
应用所需的数据,我已经帮你准备好,也上传到了网盘,你可以点击这个地址,输入提取码 ajs6 进行下载。
数据的文件名是“2011-2019 小汽车摇号数据.tar.gz”,解压之后的目录结构如下图所示。根目录下有 apply 和 lucky 两个子目录,apply 的目录内容是 2011-2019 年各个批次参与摇号的申请编号,lucky 目录包含的是各个批次中签的申请编号。方便起见,我们把参与过摇号的人叫“申请者”,把中签的人叫“中签者”。apply 和 lucky 的下一级子目录是各个摇号批次,而摇号批次目录下包含的是 Parquet 格式的数据分片。

数据的文件目录结构
apply 和 lucky 两个子目录,在逻辑上分别对应着事实表和维度表,也可以叫做“申请者表”和“中签者表”。两张表的 Schema 都是(batchNum,carNum),也就是(摇号批次,申请编号)。总之,事实表和维度表在存储方式上都做了分区设计,且分区键都是 batchNum。
准备开发环境
数据下载、解压完成之后,然后我们再来准备开发环境。首先,我们来说说开发语言。要完成“趋势分析应用”的开发,你可以结合个人偏好,使用 Python、Java、Scala 三种语言中的任意一种。由于我本人习惯使用 Scala 做开发,因此整个项目的代码都是用 Scala 实现的。如果你是 Java 或是 Python 开发者,也完全不必担心,结合后续应用逻辑的讲解与 Scala 版本的参考实现,我相信你也很快能完成应用的开发。
“趋势分析应用”非常轻量,Scala 版本的参考实现不超过 200 行代码。因此,只使用 Sublime 甚至是 VI 这样的纯文本编辑器,我们也能很快实现。不过,为了提高开发效率,以及方便后续应用的打包和部署,我还是推荐你使用集成式的 IDE,比如 IntelliJ IDEA、Eclipse、IntelliJ PyCharm 等等。IDE 的选取原则和开发语言一样,只要选择自己最顺手的就行了。
准备运行环境
最后是运行环境,由于咱们的应用比较轻量,而且数据量较小,解压之后的 Parquet 文件总大小还不超 4GB,因此,你甚至可以用手里的笔记本电脑或是台式 PC,就可以把应用从头到尾地跑通。选择“轻装上阵”主要是考虑到,不少同学可能不方便搭建分布式的物理集群,我们要确保这部分同学不会因为硬件的限制而不能参与实战。
不过,毕竟咱们这两讲的初衷和重点是性能调优实践,网络开销优化是其中关键的一环。因此,有条件的同学,我还是鼓励你搭建分布式的物理集群,或是采用云原生的分布式环境。一来这样的分布式环境更接近实际工作中的真实情况,二来调优前后的性能差异会更加地显著,有利于你加深理解不同调优技巧的作用和效果。
我这边选择了 3 台物理节点,它们的资源配置分别如下。其实,为了跑通应用和做性能对比,你并不需要这么强悍的机器配置。我这么做主要是贪图执行效率,因为想要说明不同调优技巧的作用与功效,我只需要拿到调优前后的对比结果就可以了,这样的配置可以减少我的等待时间。
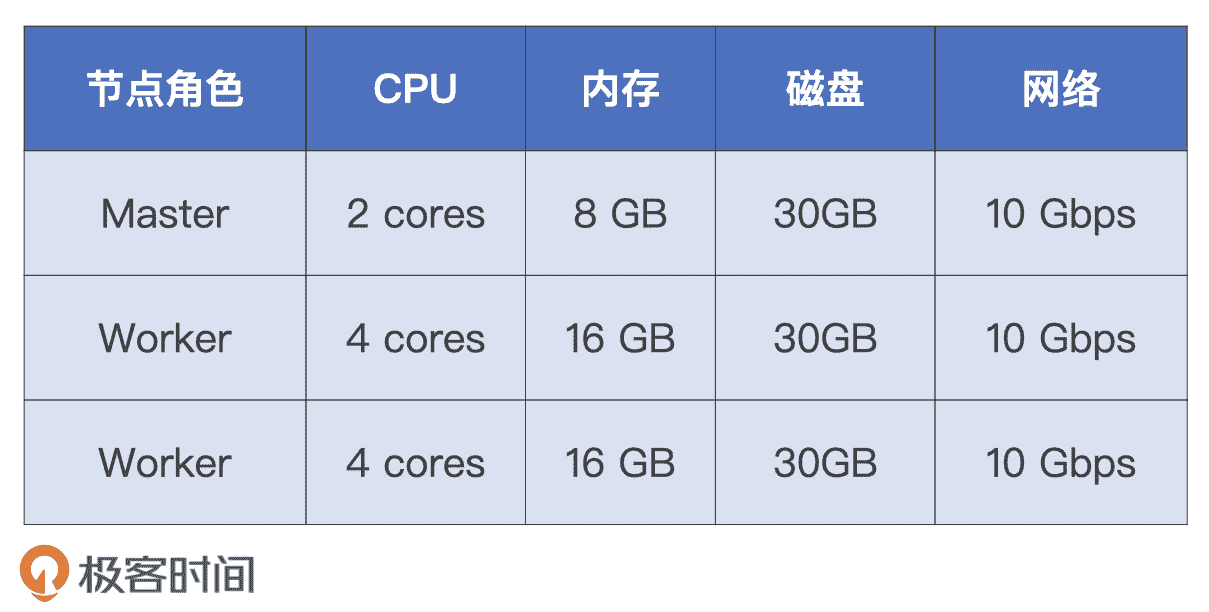
硬件资源配置
应用开发
准备好了数据、开发环境和执行环境之后,我们就步入正题,开始进行“趋势分析应用”的开发。为了解答大家关于小汽车摇号的种种困惑,在这个应用中,我们主要分析如下几个案例:
- 2011 到 2019 年底,总共有多少人参与摇号
- 摇号次数的总分布情况,以及申请者的分布情况和中签者的分布情况分别是什么
- 中签率的变化趋势是什么
- 中签率是否发生过较大变化,怎么对它做局部洞察
- 倍率高的人是否更容易中签
接下来,我们就来一一厘清这些案例的计算逻辑,并进行代码实现。
案例 1:人数统计
首先,我们需要对数据有一个基本的认知。我们先从最简单的统计计数开始,也就是统计一下截至到 2019 年底,参与摇号的总人次和幸运的中签者人数。应该说,这样的需求非常简单,我们只需使用 Parquet API 读取源文件、创建 DataFrame,然后调用 count 就可以了。
val rootPath: String = _
// 申请者数据(因为倍率的原因,每一期,同一个人,可能有多个号码)
val hdfs_path_apply = s"${rootPath}/apply"
val applyNumbersDF = spark.read.parquet(hdfs_path_apply)
applyNumbersDF.count
// 中签者数据
val hdfs_path_lucky = s"${rootPath}/lucky"
val luckyDogsDF = spark.read.parquet(hdfs_path_lucky)
luckyDogsDF.count
把这段代码丢到 spark-shell,或是打包部署到分布式环境去运行,我们很快就能够得到计算结果。截至到 2019 年底,摇号总人次为 381972118,也就是 3.8 亿人次;中签的人数是 1150828,也就是 115 万人。你可能会好奇:“摇号总人次为什么会有这么高的数量级?”
这其实并不奇怪。首先,同一个人可能参与多个批次的摇号,比如我就至少参加了 60 个批次的摇号(苦啊!)。再者,从 2016 年开始,小汽车摇号有了倍率这个概念。倍率的设计初衷,是让申请者的中签概率随着参与批次数量的增加而成比例地增加。也就是说,参与了 60 次摇号的人比仅参与 10 次摇号的人的中签概率更高。不过,官方对于倍率的实现略显简单粗暴。如果你去观察 apply 目录下 2016 年以后的批次文件就会发现,所谓的倍率实际上就是申请编号的副本数量。
正是出于以上两个原因,摇号总人次的体量才会有 3.8 亿人次。如果我们把倍率这个因素去掉,实际的摇号体量会是什么量级呢?
val applyDistinctDF = applyNumbersDF.select(“batchNum”, “carNum”).distinct
applyDistinctDF.count
以(batchNum,carNum)为粒度进行去重计数,我们就能得到实际的摇号体量是 135009819,也就是 1.35 亿人次。这意味着,从 2011 年到 2019 年这 9 年的时间里,有 1.35 亿人次参与了一项“抽奖游戏”,但是仅有 115 万人幸运中奖,摇号之难可见一斑。
案例 2:摇号次数分布
接下来,我们进一步向下追踪(Drill Down),挖掘一下不同人群摇号次数的分布,也就是统计所有申请者累计参与了多少次摇号,所有中签者摇了多少次号才能幸运地摇中签。对于这两个统计计算,我们需要消除倍率的影响。也就是说,同一个申请编号在同一个批次中应该只保留一份副本。因此,我们需要使用去重之后的“申请者表”:applyDistinctDF。
场景 1:参与摇号的申请者
首先,我们先来分析所有申请者的分布情况,当然也包括中签者。根据刚刚介绍的“业务需求”,我们很快就能写出相应的查询语句。
val result02_01 = applyDistinctDF
.groupBy(col(“carNum”))
.agg(count(lit(1)).alias(“x_axis”))
.groupBy(col(“x_axis”))
.agg(count(lit(1)).alias(“y_axis”))
.orderBy(“x_axis”)
result02_01.write.format(“csv”).save("_")
将上述代码付诸执行,我们会得到如下图所示的计算结果。其中,横坐标代表申请者参与过的摇号批次次数,纵坐标是对应的参与人数。从 2011 年到 2013 年,摇号是每月一次的。而从 2014 开始,摇号是每两个月一次的。因此,截至到 2019 年底,总共有 72(12 * 3 + 6 * 6)次摇号。所以,我们看到横坐标的值域是从 1 到 72,1 表示摇过 1 次的人,72 就比较惨了,它表示摇过 72 次的人。
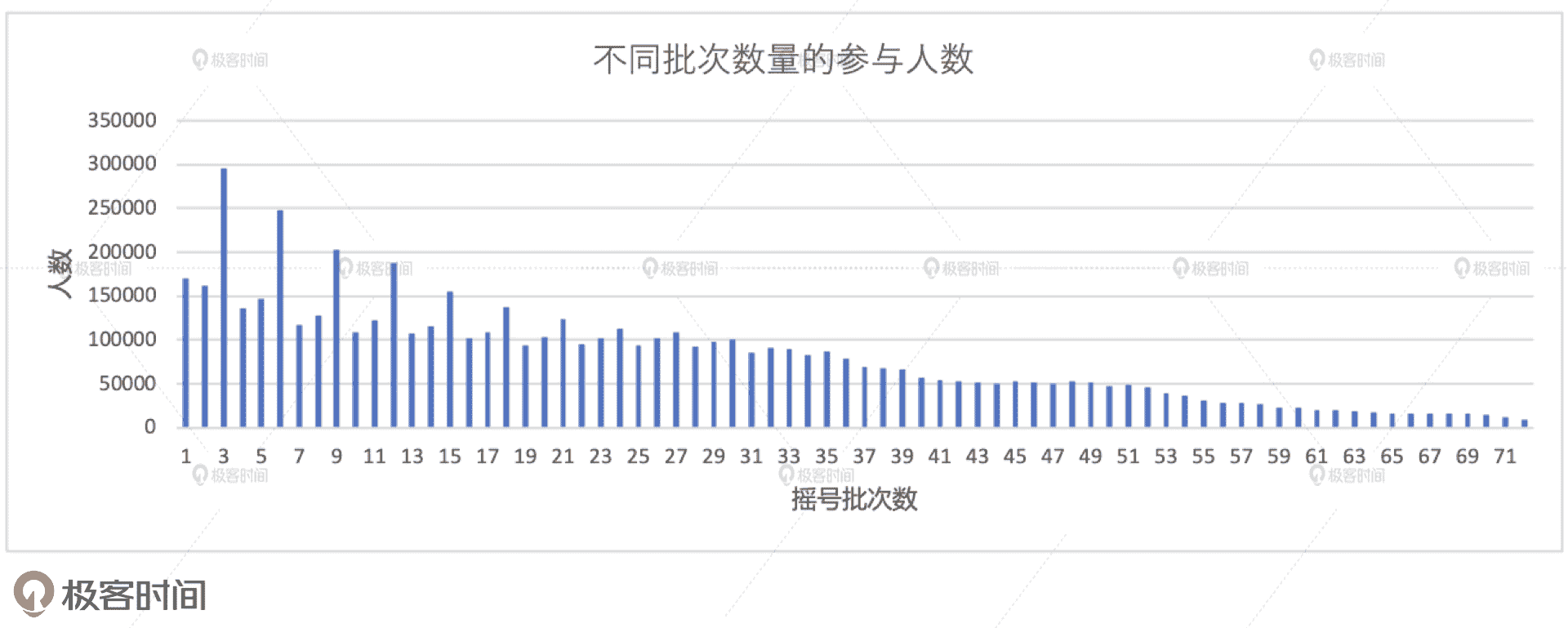
从图中我们不难发现,随着摇号次数的逐级递增,人数分布基本上呈现出了逐级递减的趋势。那这意味着什么呢?这意味着每隔两个月就会有新人从驾校毕业,加入到庞大的摇号大军中来。仔细观察上图的左半部分我们会发现,摇号次数凡是遇到 3 的倍数,对应的人数往往比其“左邻右舍”多出甚至两倍,这是为什么呢?
我们刚刚说过,从 2014 年开始,摇号是每两个月进行一次。因此,摇号次数相差 3 则意味着两次摇号之间的时间差是半年左右。比如说,摇了 3 次的人就比摇了 6 次的人晚半年加入摇号大军。那么,半年意味着什么呢?我们不妨脑洞一下,尽管每个月都有从驾校毕业的学员,但是,寒暑假往往是大批量“生产”学员的高峰时期,而寒暑假恰好相差半年左右。你觉得我这个推测合理吗?
场景 2:幸运的中签者
接下来,我们再来看看,那些中签的幸运儿们到底有多幸运?要想得到中签者的摇号次数,我们需要把 applyDistinctDF 和 luckyDogsDF 两张表做内关联,然后再做分组、聚合,代码实现如下表所示。
val result02_02 = applyDistinctDF
.join(luckyDogsDF.select(“carNum”), Seq(“carNum”), “inner”)
.groupBy(col(“carNum”)).agg(count(lit(1)).alias(“x_axis”))
.groupBy(col(“x_axis”)).agg(count(lit(1)).alias(“y_axis”))
.orderBy(“x_axis”)
result02_02.write.format(“csv”).save("_")
将上述代码付诸执行,我们会得到如下图所示的计算结果,其中横纵坐标的含义与场景 1 一样,分别是摇号批次数和对应的人数分布。我们发现,随着摇号次数的逐级递增,人数的分布完全是单调递减的。也就是说,摇号的次数越多,中签者的数量越少。我能想到的一个原因是,摇号的次数越高,对应的参与人数就越少,这一点在场景 1 已经得到了验证。这个其实也不难理解,能一直坚持摇 60 次以上的玩家,真的都是骨灰级玩家。那么,参与的人基数小,中签者的数量自然就更少。
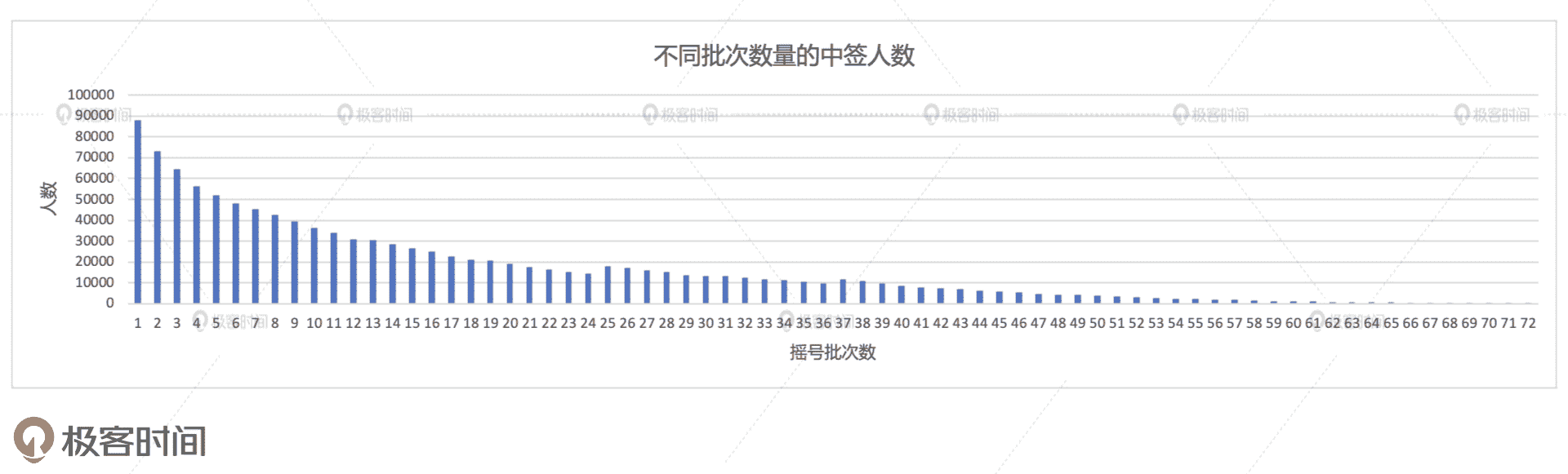
不过,如果假设申请者两个月摇一次号,那么我们就会得出一个非常扎心的结论:摇号中签的人往往不需要等待太长的时间,绝大多数都是在 2-3 年内摇中了购车资格,因为前半部分的总数占到了绝大多数。而等待 3 年以上才摇上号的人,反而成了幸运儿群体中的“少数派”。这不禁让我想起了当年大家开玩笑的那句话:“你要是人品够用,早就该摇上了。超过 3 年还没摇上,就说明你人品余额不足,摇号这件事以后也就不用指望了”。
案例 3:中签率的变化趋势
从摇号次数的分布来看,申请者和中签者的变化趋势是一致的,那这是否意味着二者相除之后的比例是稳定的呢?二者的商实际上就是中签率。接下来,我们就去探究一下中签率的变化趋势。要计算中签率,我们需要分别统计每一个摇号批次中的申请者和中签者人数,然后再把它们做关联、聚合,代码实现如下所示。
// 统计每批次申请者的人数
val apply_denominator = applyDistinctDF
.groupBy(col(“batchNum”))
.agg(count(lit(1)).alias(“denominator”))
// 统计每批次中签者的人数
val lucky_molecule = luckyDogsDF
.groupBy(col(“batchNum”))
.agg(count(lit(1)).alias(“molecule”))
val result03 = apply_denominator
.join(lucky_molecule, Seq(“batchNum”), “inner”)
.withColumn(“ratio”, round(col(“molecule”)/col(“denominator”), 5))
.orderBy(“batchNum”)
result03.write.format(“csv”).save("_")
我们得到的中签率示意图如下所示。其中,横坐标为各个摇号批次,从 201101 到 201906,也就是从 2011 年的第一批到 2019 年的第 72 批,纵坐标就是中签率。从中我们可以很直观地看到,随着摇号批次的推进,中签率呈锐减的趋势。201101 批次的中签率在 9.4% 左右,不到 10%。而 201906 批次的中签率为 1.9‰,也就是千分之一点九。这么看来,1000 个人里面能摇上号的还凑不够两个人,这也难怪摇号如此之难了。
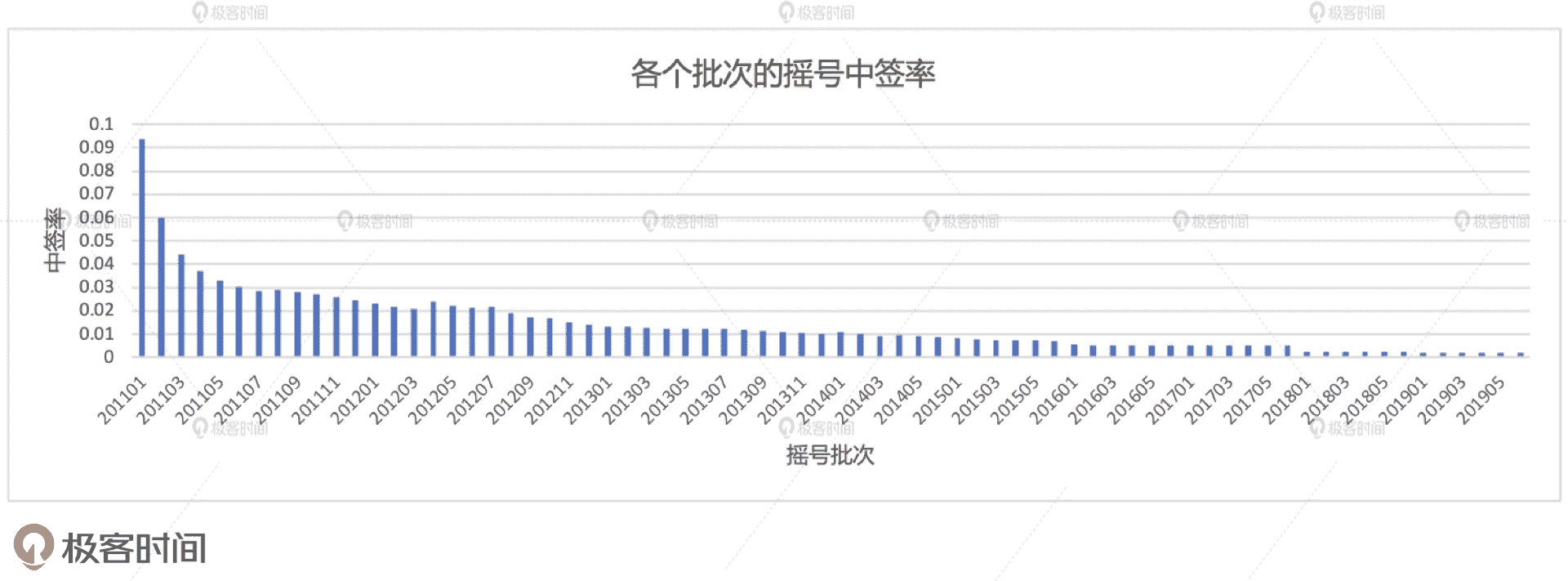
案例 4:中签率局部洞察
第 4 个案例与案例 3 的区别在于,我们只关注 2018 年的中签率变化趋势。这样做的原因有二:一来,通过计算和对比,我发现 2018 年的中签率相比 2017 年几乎经历了“断崖式”的下跌,因此我想给 2018 年一个特写;二来,只关注 2018 年的数据,可以让我们有机会对比启用 AQE Join 策略调整前后的性能差异。
基于案例 3 的代码实现,要关注 2018 年,我们只需要在 batchNum 之上添加个过滤条件就好了。
// 筛选出 2018 年的中签数据,并按照批次统计中签人数
val lucky_molecule_2018 = luckyDogsDF
.filter(col(“batchNum”).like(“2018%”))
.groupBy(col(“batchNum”))
.agg(count(lit(1)).alias(“molecule”)) 与
// 通过与筛选出的中签数据按照批次做关联,计算每期的中签率
val result04 = apply_denominator
.join(lucky_molecule_2018, Seq(“batchNum”), “inner”)
.withColumn(“ratio”, round(col(“molecule”)/col(“denominator”), 5))
.orderBy(“batchNum”)
result04.write.format(“csv”).save("_")
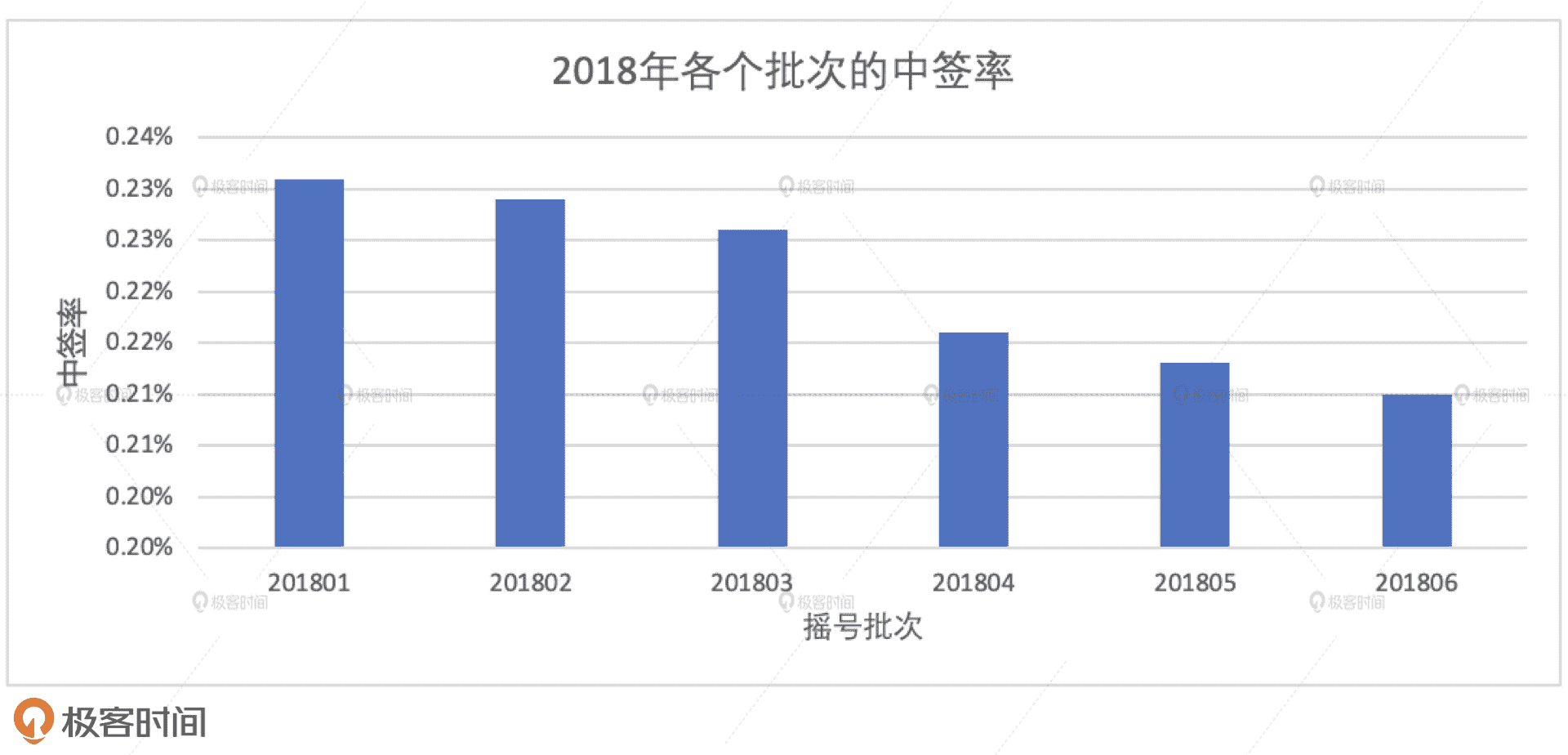
结合案例 3 与案例 4 的执行结果,我们至少有两点发现。第一点,2018 年内各批次中签率下降较为平缓,从 201801 批次的 2.3‰下降至 201806 批次的 2.1‰,整体下降幅度不超过 10%。第二点,2017 年最后一个批次,也就是 201706 批次的中签率在 4.9‰左右,而 201801 批次的中签率为 2.3‰,在短短两个月之内,中签率惨遭“腰斩”,并在接下来的两年里,一路阴跌,最终在 201906 批次破掉 2‰。
案例 5:倍率分析
那么,在中签率如此之低的情况下,倍率这玩意还有意义吗?接下来,我们先去探索倍率的分布情况,然后再去观察,不同倍率的人群,他们的中签比例是怎样分布的。
场景 1:不同倍率下的中签人数
我们先来统计一下,那些有幸中签的人分别是在多大的倍率下中签的。从 2016 年开始,才有倍率这个概念,因此,对于倍率的统计,我们只需要关注 2016 年以后的摇号数据即可。对于同一个中签者,他在不同批次的倍率可能是不同的,我们只需要拿到其中最大的倍率参与统计就可以了。原因很简单,最大的倍率就是她 / 他中签之前的倍率。
另外,倍率的计算需要依赖原始的多副本摇号数据,所以这里我们不能再使用去重的摇号数据,而应该用包含重复申请编号的 applyNumbersDF 表。基于这样的逻辑,我们的代码实现如下。
val result05_01 = applyNumbersDF
.join(luckyDogsDF.filter(col(“batchNum”) >= “201601”)
.select(“carNum”), Seq(“carNum”), “inner”)
.groupBy(col(“batchNum”),col(“carNum”))
.agg(count(lit(1)).alias(“multiplier”))
.groupBy(“carNum”)
.agg(max(“multiplier”).alias(“multiplier”))
.groupBy(“multiplier”)
.agg(count(lit(1)).alias(“cnt”))
.orderBy(“multiplier”)
result05_01.write.format(“csv”).save("_")
中签者的倍率分布如下图所示。其中,横坐标为中签者的倍率,更准确地说,是中签者在参与的摇号批次中最大的副本数量,纵坐标是人数分布。通过观察执行结果我们不难发现,中签者的倍率呈现明显的正态分布。因此,从这张图我们可以得到初步结论:要想摇中车牌号,你并不需要很高的倍率。换句话说,对于中签这件事来说,倍率的作用和贡献并不是线性递增的。
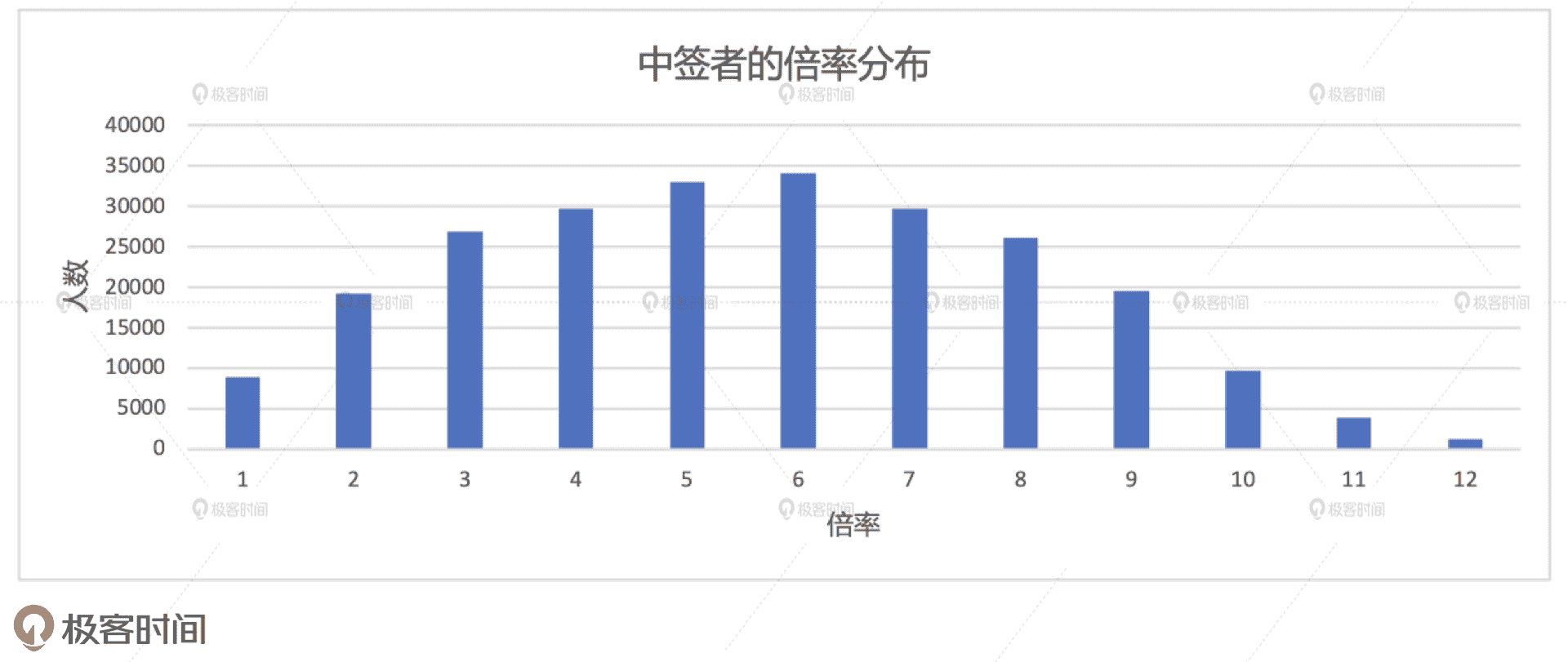
不过,和案例 2 类似,这里同样存在一个基数的问题。也就是说,倍率高的人本来就少,其中的中签者数量自然也少。因此,我们还要结合申请者的倍率分布,去计算不同倍率下的中签比例,才能更加完备地对倍率的作用下结论。
场景 2:不同倍率下的中签比例
对倍率分布有了初步认知之后,我们再来计算不同倍率人群的中签比例,去探究倍率本身对于中签的贡献究竟有多大。有了场景 1 中签者的倍率分布,我们只需要去计算申请者的倍率分布,然后把两份数据做关联、聚合,就可以得到我们想要的结果。
// Step01: 过滤出 2016-2019 申请者数据,统计出每个申请者在每一期内的倍率,并在所有批次中选取最大的倍率作为申请者的最终倍率,最终算出各个倍率下的申请人数
val apply_multiplier_2016_2019 = applyNumbersDF
.filter(col(“batchNum”) >= “201601”)
.groupBy(col(“batchNum”), col(“carNum”))
.agg(count(lit(1)).alias(“multiplier”))
.groupBy(“carNum”)
.agg(max(“multiplier”).alias(“multiplier”))
.groupBy(“multiplier”)
.agg(count(lit(1)).alias(“apply_cnt”))
// Step02: 将各个倍率下的申请人数与各个倍率下的中签人数左关联,并求出各个倍率下的中签率
val result05_02 = apply_multiplier_2016_2019
.join(result05_01.withColumnRenamed(“cnt”, “lucy_cnt”), Seq(“multiplier”), “left”)
.na.fill(0)
.withColumn(“ratio”, round(col(“lucy_cnt”)/col(“apply_cnt”), 5))
.orderBy(“multiplier”)
result05_02.write.format(“csv”).save("_")
不同倍率下的中签比例如下图所示。其中横坐标为倍率,纵坐标有两个。蓝色柱状图体代表中签人数,它的分布与场景 1 的分布是一致的;绿色柱状条表示的是中签比例,它表示在同一个倍率下,中签人数与申请人数的比值。
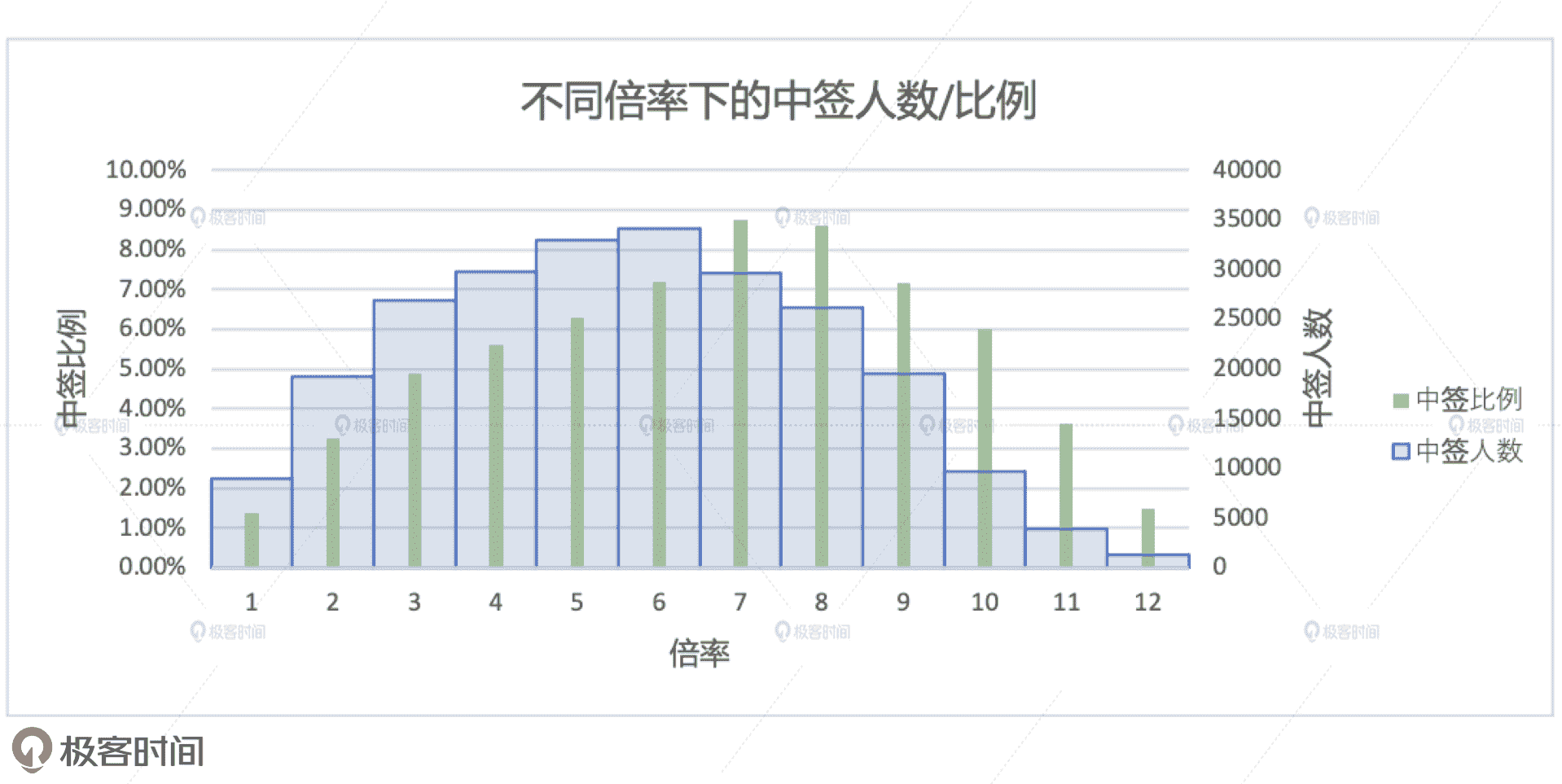
与中签人数一样,中签比例在不同的倍率下,也呈现出了正态分布。有了这份数据做补充,我们可以夯实场景 1 中得出的结论。也就是,倍率对中签的贡献极其有限。这个结论很好地解释了,为什么摇号很久,倍率很高的人也难以中签。
到此为止,通过以上几个案例的分析,我们就对摇号次数分布、中签率变化趋势、倍率分布与中签比例有了答案。
小结
今天这一讲,我们重点开发了一个趋势分析应用,来解答北京市小汽车摇号的各个问题。这个应用主要实现了 5 个案例,分别是摇号次数分布、中签率变化趋势、中签率的大变动、倍率分布与中签比例。为了方便理解,我把它们要解决的问题、答案、主要的实现思路都总结在了下面的脑图中,你可以看一看。

至于这 5 个案例的代码实现和执行结果,我把它们都上传到了公用的 GitHub 仓库,你可以从这个地址获取完整内容。
当然,目前的代码肯定存在很多可以优化的地方,至于怎么优化,我先卖个关子,下一讲再详细来说。
每日一练
- 如果让你来实现小汽车摇号的倍率机制,你觉得怎么实现才更严谨呢?
- 基于这份 2011-2019 的小汽车摇号数据,你还能想到哪些有意思的洞察、视角和案例,值得我们进一步去探索呢?
- 你认为,倍率对于中签的贡献和作用微乎其微的原因是什么呢?
期待在留言区看到你的思考和答案,我们下一讲见!
文章作者
上次更新 2025-01-03