特别加餐|倒排检索加速(一):工业界如何利用跳表、哈希表、位图进行加速?
文章目录
你好,我是陈东。欢迎来到检索专栏的第一次加餐时间。
很多同学在留言区提问,说基础篇讲了这么多检索的基础数据结构和算法,那它们在工业界的实际系统中是怎么应用的呢?真正的检索系统和算法又是什么样的呢?
为了帮助你把这些基础的知识,更好地和实际应用结合。我特别准备了两篇加餐,来和你一起聊一聊,这些看似简单的基础技术是怎样在工业界的实际系统中发挥重要作用的。
在许多大型系统中,倒排索引是最常用的检索技术,搜索引擎、广告引擎、推荐引擎等都是基于倒排索引技术实现的。而在倒排索引的检索过程中,两个 posting list 求交集是一个最重要、最耗时的操作。
所以,今天我们就先来看一看,倒排索引在求交集的过程中,是如何借助跳表、哈希表和位图,这些基础数据结构进行加速的。
跳表法加速倒排索引
在第 5 讲中我们讲过,倒排索引中的 posting list 一般是用链表来实现的。当两个 posting list A 和 B 需要合并求交集时,如果我们用归并法来合并的话,时间代价是 O(m+n)。其中,m 为 posting list A 的长度,n 为 posting list B 的长度。
那对于这个归并过程,工业界是如何优化的呢?接下来,我们就通过一个例子来看一下。
假设 posting list A 中的元素为 <1,2,3,4,5,6,7,8……,1000>,这 1000 个元素是按照从 1 到 1000 的顺序递增的。而 posting list B 中的元素,只有 <1,500,1000>3 个。那按照我们之前讲过的归并方法,它们的合并过程就是,在找到相同元素 1 以后,还需要再遍历 498 次链表,才能找到第二个相同元素 500。
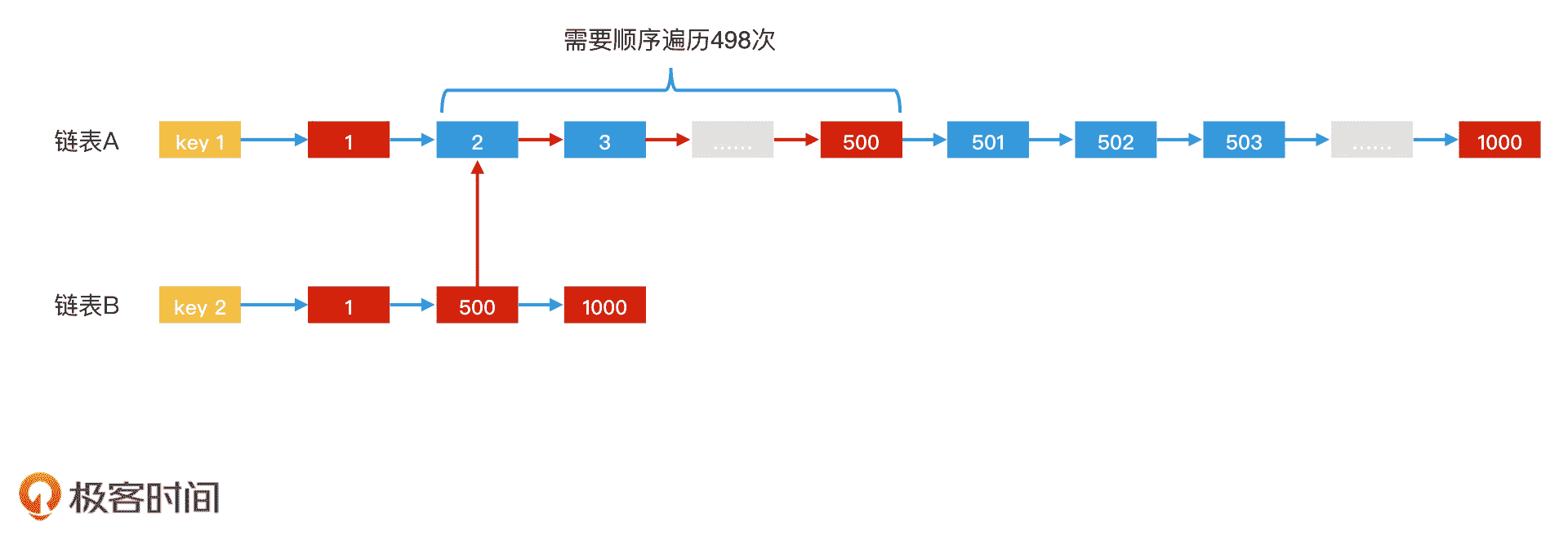
链表遍历,时间代价高
很显然,为了找到一个元素,遍历这么多次是很不划算的。那对于链表遍历,我们可以怎么优化呢?实际上,在许多工业界的实践中,比如搜索引擎,还有 Lucene 和 Elasticsearch 等应用中,都是使用跳表来实现 posting list 的。
在上面这个例子中,我们可以将链表改为跳表。这样,在 posting list A 中,我们从第 2 个元素遍历到第 500 个元素,只需要 log(498) 次的量级,会比链表快得多。

跳表查找,检索加速
这个时候你可能就会问了,我们只能用 B 中的每一个元素去 A 中二分查找吗?那在解答这个问题之前,我们先来看下图这个例子。
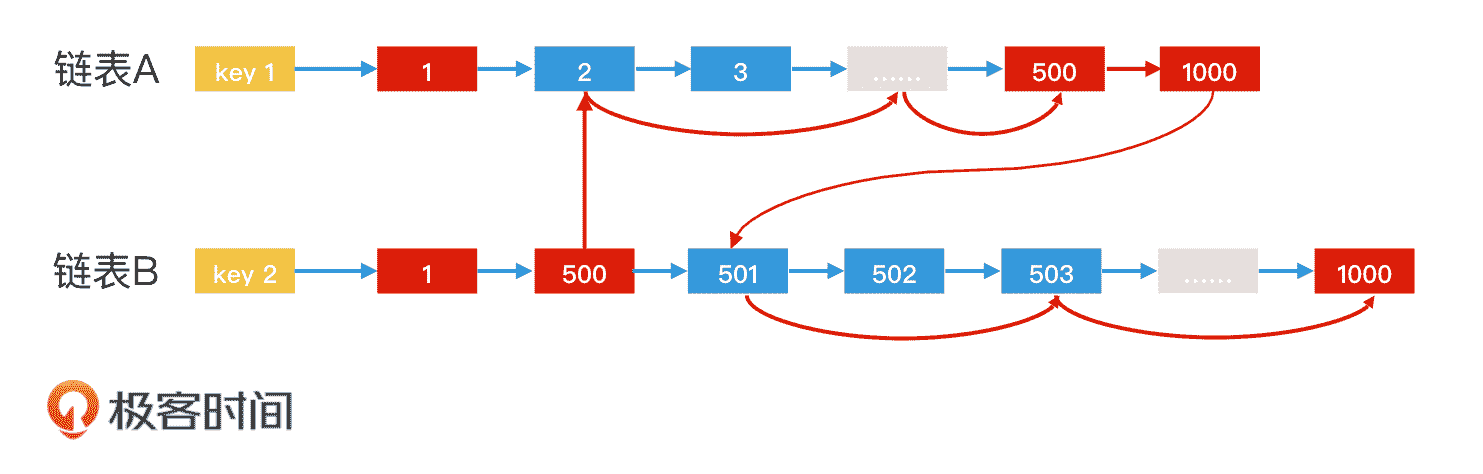
相互二分查找
你会发现,在寻找 500 这个公共元素的过程中,我们是拿着链表 B 中的 500 作为 key,在链表 A 中进行跳表二分查找的。但是,在查找 1000 这个公共元素的过程中,我们是拿着链表 A 中的元素 1000,在链表 B 中进行跳表二分查找的。
我们把这种方法定义为相互二分查找。那啥叫相互二分查找呢?
你可以这么理解:如果 A 中的当前元素小于 B 中的当前元素,我们就以 B 中的当前元素为 key,在 A 中快速往前跳;如果 B 中的当前元素小于 A 中的当前元素,我们就以 A 中的当前元素为 key,在 B 中快速往前跳。这样一来,整体的检索效率就提升了。
在实际的系统中,如果 posting list 可以都存储在内存中,并且变化不太频繁的话,那我们还可以利用可变长数组来代替链表。
可变长数组的数组的长度可以随着数据的增加而增加。一种简单的可变长数组实现方案就是当数组被写满时,我们直接重新申请一个 2 倍于原数组的新数组,将原数组数据直接导入新数组中。这样,我们就可以应对数据动态增长的场景。
那对于两个 posting list 求交集,我们同样可以先使用可变长数组,再利用相互二分查找进行归并。而且,由于数组的数据在内存的物理空间中是紧凑的,因此 CPU 还可以利用内存的局部性原理来提高检索效率。
哈希表法加速倒排索引
说到高效查询,哈希表 O(1) 级别的查找能力令人印象深刻。那我们有没有能利用哈希表来加速的方法呢?别说,还真有。
哈希表加速的思路其实很简单,就是当两个集合要求交集时,如果一个集合特别大,另一个集合相对比较小,那我们就可以用哈希表来存储大集合。这样,我们就可以拿着小集合中的每一个元素去哈希表中对比:如果查找为存在,那查找的元素就是公共元素;否则,就放弃。
我们还是以前面说的 posting list A 和 B 为例,来进一步解释一下这个过程。由于 Posting list A 有 1000 个元素,而 B 中只有 3 个元素,因此,我们可以将 posting list A 中的元素提前存入哈希表。这样,我们利用 B 中的 3 个元素来查询的时候,每次查询代价都是 O(1)。如果 B 有 m 个元素,那查询代价就是 O(m)。

将 posting list A 中的元素提前存入哈希表
但是,使用哈希表法加速倒排索引有一个前提,就是我们要在查询发生之前,就把 posting list 转为哈希表。这就需要我们提前分析好,哪些 posting list 经常会被拿来求交集,针对这一批 posting list,我们将它们提前存入哈希表。这样,我们就能实现检索加速了。
这里还有一点需要你注意,原始的 posting list 我们也要保留。这是为什么呢?
我们假设有这样一种情况:当我们要给两个 posting list 求交集时,发现这两个 posting list 都已经转为哈希表了。这个时候,由于哈希表没有遍历能力,反而会导致我们无法合并这两个 posting list。因此,在哈希表法的最终改造中,一个 key 后面会有两个指针,一个指向 posting list,另一个指向哈希表(如果哈希表存在)。
除此之外,哈希表法还需要在有很多短 posting list 存在的前提下,才能更好地发挥作用。这是因为哈希表法的查询代价是 O(m),如果 m 的值很大,那它的性能就不一定会比跳表法更优了。
位图法加速倒排索引
我们知道,位图其实也可以看作是一种特殊的哈希,所以除了哈希表,我们还可以使用位图法来改造链表。如果我们使用位图法,就需要将所有的 posting list 全部改造为位图,这样才能使用位图的位运算来进行检索加速。那具体应该怎么做呢?我们一起来看一下。
首先,我们需要为每个 key 生成同样长度的位图,表示所有的对象空间。然后,如果一个元素出现在该 posting list 中,我们就将位图中该元素对应的位置置为 1。这样就完成了 posting list 的位图改造。
接下来,我们来看一下位图法的查询过程。
如果要查找 posting list A 和 B 的公共元素,我们可以将 A、B 两个位图中对应的位置直接做 and 位运算(复习一下 and 位运算:0 and 0 = 0;0 and 1 = 0;1 and 1 = 1)。由于位图的长度是固定的,因此两个位图的合并运算时间代价也是固定的。并且由于 CPU 执行位运算的效率非常快,因此,在位图总长度不是特别长的情况下,位图法的检索效率还是非常高的。

位运算
和哈希表法一样,位图法也有自己的局限性。我总结了以下 3 点,你可以感受一下。
- 位图法仅适用于只存储 ID 的简单的 posting list。如果 posting list 中需要存储复杂的对象,就不适合用位图来表示 posting list 了。
- 位图法仅适用于 posting list 中元素稠密的场景。对于 posting list 中元素稀疏的场景,使用位图的运算和存储开销反而会比使用链表更大。
- 位图法会占用大量的空间。尽管位图仅用 1 个 bit 就能表示元素是否存在,但每个 posting list 都需要表示完整的对象空间。如果 ID 范围是用 int32 类型的数组表示的,那一个位图的大小就约为 512M 字节。如果我们有 1 万个 key,每个 key 都存一个这样的位图,那就需要 5120G 的空间了。这是非常可怕的空间开销啊!
在很多成熟的工业界系统中,为了解决位图的空间消耗问题,我们经常会使用一种压缩位图的技术 Roaring Bitmap 来代替位图。在数据库、全文检索 Lucene、数据分析 Druid 等系统中,你都能看到 Roaring Bitmap 的身影。
升级版位图:Roaring Bitmap
下面我们来学习一下 Roaring Bitmap 的设计思想。
首先,Roaring Bitmap 将一个 32 位的整数分为两部分,一部分是高 16 位,另一部分是低 16 位。对于高 16 位,Roaring Bitmap 将它存储到一个有序数组中,这个有序数组中的每一个值都是一个“桶”;而对于低 16 位,Roaring Bitmap 则将它存储在一个 2^16 的位图中,将相应位置置为 1。这样,每个桶都会对应一个 2^16 的位图。
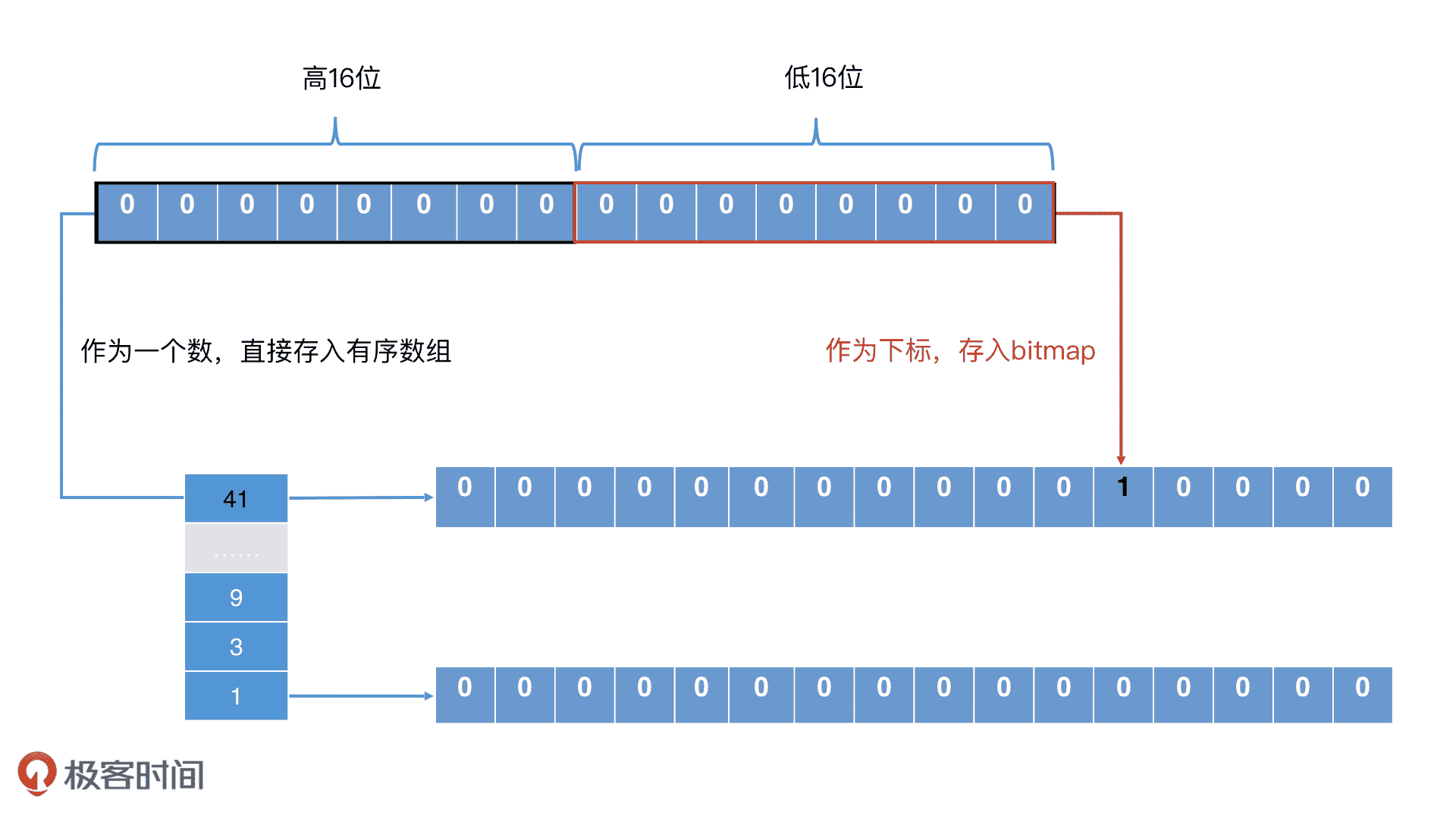
Roaring Bitmap 存储过程
接下来,如果我们要确认一个元素是否在 Roaring Bitmap 中存在,通过两次查找就能确认了。第一步是以高 16 位在有序数组中二分查找,看对应的桶是否存在。如果存在,第二步就是将桶中的位图取出,拿着低 16 位在位图中查找,判断相应位置是否为 1。第一步查找由于是数组二分查找,因此时间代价是 O(log n);第二步是位图查找,因此时间代价是 O(1)。
所以你看,这种将有序数组和位图用倒排索引结合起来的设计思路,是能够保证高效检索的。那它到底是怎么节省存储空间的呢?
我们来看一个极端的例子。
如果一个 posting list 中,所有元素的高 16 位都是相同的,那在有序数组部分,我们只需要一个 2 个字节的桶(注:每个桶都是一个 short 型的整数,因此只有 2 个字节。如果数组提前分配好了 2^16 个桶,那就需要 128K 字节的空间,因此使用可变长数组更节省空间)。在低 16 位部分,因为位图长度是固定的,都是 2^16 个 bit,那所占空间就是 8K 个字节。
同样都是 32 位的整数,这样的空间消耗相比于我们在位图法中计算的 512M 字节来说,大大地节省了空间!
你会发现,相比于位图法,这种设计方案就是通过,将不存在的桶的位图空间全部省去这样的方式,来节省存储空间的。而代价就是将高 16 位的查找,从位图的 O(1) 的查找转为有序数组的 log(n) 查找。
那每个桶对应的位图空间,我们是否还能优化呢?
前面我们说过,当位图中的元素太稀疏时,其实我们还不如使用链表。这个时候,链表的计算更快速,存储空间也更节省。Roaring Bitmap 就基于这个思路,对低 16 位的位图部分进行了优化:如果一个桶中存储的数据少于 4096 个,我们就不使用位图,而是直接使用 short 型的有序数组存储数据。同时,我们使用可变长数组机制,让数组的初始化长度是 4,随着元素的增加再逐步调整数组长度,上限是 4096。这样一来,存储空间就会低于 8K,也就小于使用位图所占用的存储空间了。
总结来说,一个桶对应的存储容器有两种,分别是数组容器和位图容器(其实还有一种压缩的 runContainer,它是对连续元素通过只记录初始元素和后续个数。由于它不是基础类型,需要手动调用 runOptimize() 函数才会启用,这里就不展开说了)。那在实际应用的过程中,数组容器和位图容器是如何转换的呢?这里有三种情况。
第一种,在一个桶中刚插入数据时,因为数据量少,所以我们就默认使用数组容器;
第二种,随着数据插入,桶中的数据不断增多,当数组容器中的元素个数大于 4096 个时,就从数组容器转为位图容器;
第三种,随着数据的删除,如果位图容器中的元素个数小于 4096 个,就退化回数组容器。
这个过程是不是很熟悉?没错,这很像第 3节中的 Hashmap 的处理方法。
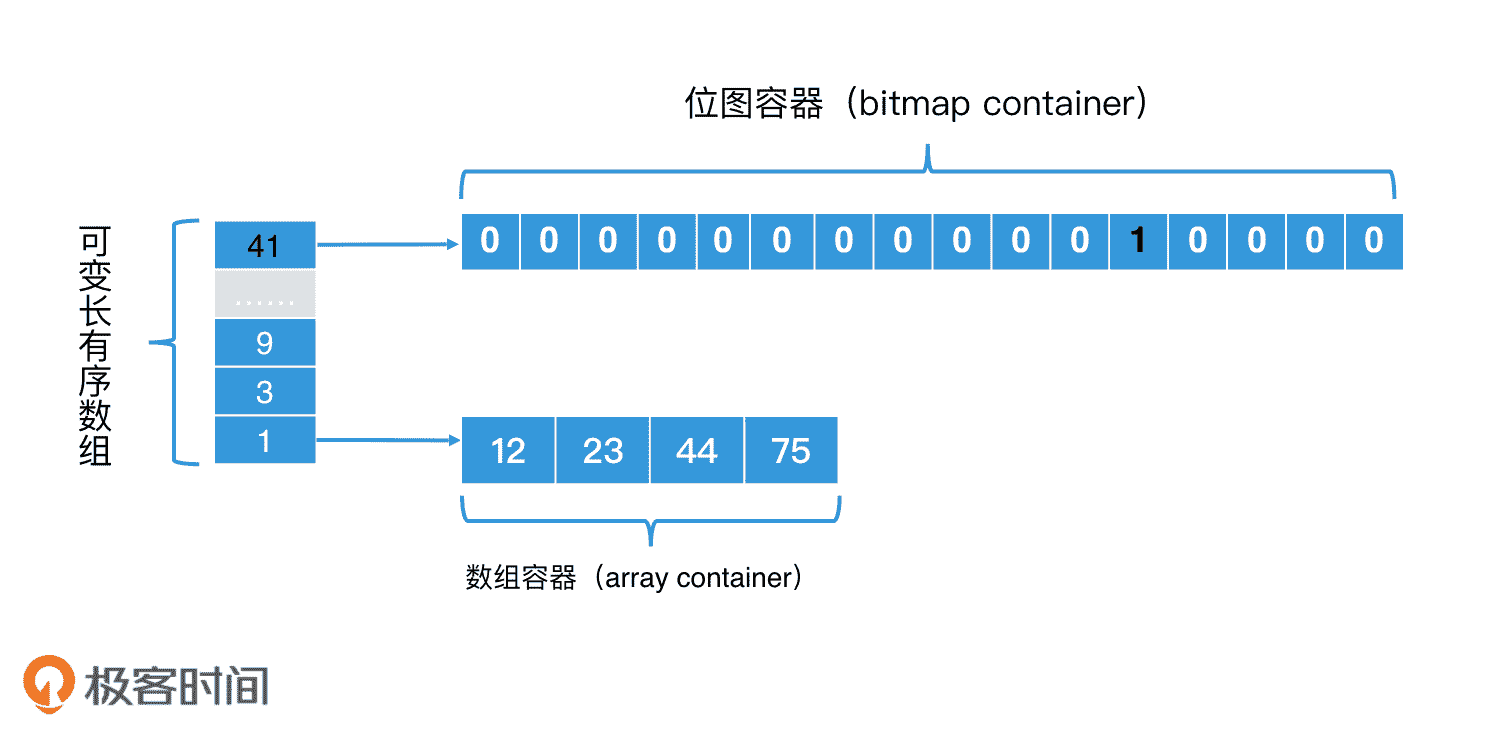
使用数组容器和位图容器并可以相互转换
好了,前面我们说了这么多 Roaring Bitmap 的压缩位图空间的设计思路。下面,我们回到两个集合 A 和 B 快速求交集的例子中,一起来看一看 Roaring Bitmap 是怎么做的。假设,这里有 Roaring Bitmap 表示的两个集合 A 和 B,那我们求它们交集的过程可以分为 2 步。
第 1 步,比较高 16 位的所有桶,也就是对这两个有序数组求交集,所有相同的桶会被留下来。
第 2 步,对相同的桶里面的元素求交集。这个时候会出现 3 种情况,分别是位图和位图求交集、数组和数组求交集、位图和数组求交集。
其中,位图和位图求交集,我们可以直接使用位运算;数组和数组求交集,我们可以使用相互二分查找(类似跳表法);位图和数组求交集,我们可以通过遍历数组,在位图中查找数组中的每个元素是否存在(类似哈希表法)。这些方法我们前面都讲过了,那知道了方法,具体怎么操作就是很容易的事情了,你可以再自己尝试一下。
重点回顾
好了,今天的内容讲完了。我们来总结一下,你要掌握的重点内容。
在工业界,我们会利用跳表法、哈希表法和位图法,对倒排索引进行检索加速。
其中,跳表法是将实现倒排索引中的 posting list 的链表改为了跳表,并且使用相互二分查找来提升检索效率;哈希表法就是在有很多短 posting list 存在的前提下,将大的 posting list 转为哈希表,减少查询的时间代价;位图法是在位图总长度不是特别长的情况下,将所有的 posting list 都转为位图,它们进行合并运算的时间代价由位图的长度决定。
并且我们还介绍了位图的升级版本,Roaring Bitmap。很有趣的是,你会发现 Roaring Bitmap 求交集过程的设计实现,本身就是跳表法、哈希表法和位图法的一个综合应用案例。
最后呢,我还想再多说两句。实际上,我写这篇文章就是想告诉你,基础的数据结构和算法组合在一起,就能提供更强大的检索能力,而且这也是大量的工程系统中广泛使用的设计方案。因此,深入理解每一种基础数据结构和算法的特点和适用场景,并且能将它们灵活应用,这能帮助你更好地学习和理解复杂的数据结构和算法,以及更好地学会如何设计复杂的高性能检索系统。
课堂讨论
最后,我们还是来看一道讨论题。
在 Roaring Bitmap 的求交集过程中,有位图和位图求交集、数组和数组求交集、位图和数组求交集这 3 种场景。那它们求交集以后的结果,我们是应该用位图来存储,还是用数组来存储呢?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这篇文章分享给你的朋友。
文章作者 anonymous
上次更新 2024-01-23