特别加餐|倒排检索加速(二):如何对联合查询进行加速?
文章目录
你好,我是陈东。欢迎来到检索专栏的第二次加餐时间。
在上一篇加餐中,我们讲了工业界中,倒排索引是怎么利用基础的数据结构来加速“求交集”过程的。现在,相信你已经对跳表、哈希表和位图的实际使用,有了更深刻的理解和认识了。然而,在日常的检索中,我们往往会面临更复杂的联合查询需求。这个时候,又该如何加速呢?
我们先来看一个例子:在一个系统的倒排索引中,有 4 个不同的 key,分别记录着“北京”“上海”“安卓”“学生”,这些标签分别对应着 4 种人群列表。如果想分析用户的特点,我们需要根据不同的标签来选择不同的人群。这个时候,我们可能会有以下的联合查询方式:
- 在“北京”或在“上海”,并且使用“安卓”的用户集合。抽象成联合查询表达式就是,(“北京”∪“上海”)∩“安卓”;
- 在“北京”使用“安卓”,并且是“学生”的用户集合。抽象成联合查询表达式就是,“北京”∩“安卓”∩“学生”。
这只是 2 个比较有代表性的联合查询方式,实际上,联合查询的组合表达可以更长、更复杂。对于联合查询,在工业界中有许多加速检索的研究和方法,比如,调整次序法、快速多路归并法、预先组合法和缓存法。今天,我们就来聊一聊这四种加速方法。
方法一:调整次序法
首先,我们来看调整次序法。那什么是调整次序法呢?接下来,我们就以三个集合的联合查询为例,来一起分析一下。这里我再多说一句,虽然这次讲的是三个集合,但是对于多个集合,我们也是采用同样的处理方法。
假设,这里有 A、B、C 三个集合,集合中的元素个数分别为 2、20、40,而且 A 包含在 B 内,B 包含在 C 内。这里我先补充一点,如果两个集合分别有 m 个元素和 n 个元素,那使用普通的遍历归并合并它们的时间代价为 O(m+n)。接着,如果我们要对 A、B、C 求交集,这个时候,会有几种不同的求交集次序,比如,A∩(B∩C)、(A∩B)∩C 等。那我们该如何选择求交集的次序呢?下面,我们就以这两种求交集次序为例来分析一下,不同的求交集次序对检索效率的影响。
当求交集次序是 A∩(B∩C)时,我们要先对 B 和 C 求交集,时间代价就是 20+40 = 60,得到的结果集是 B,然后 B 再和 A 求交集,时间代价是 2 + 20 = 22。因此,最终一共的时间代价就是 60 + 22 = 82。
那当求交集次序是(A∩B)∩C 时,我们要先对 A 和 B 求交集,时间代价是 2 + 20 = 22,得到的结果集是 A,然后 A 再和 C 求交集,时间代价是 2 + 40 = 42。因此,最终的时间代价就是 22 + 42 = 64。这比之前的代价要小得多。
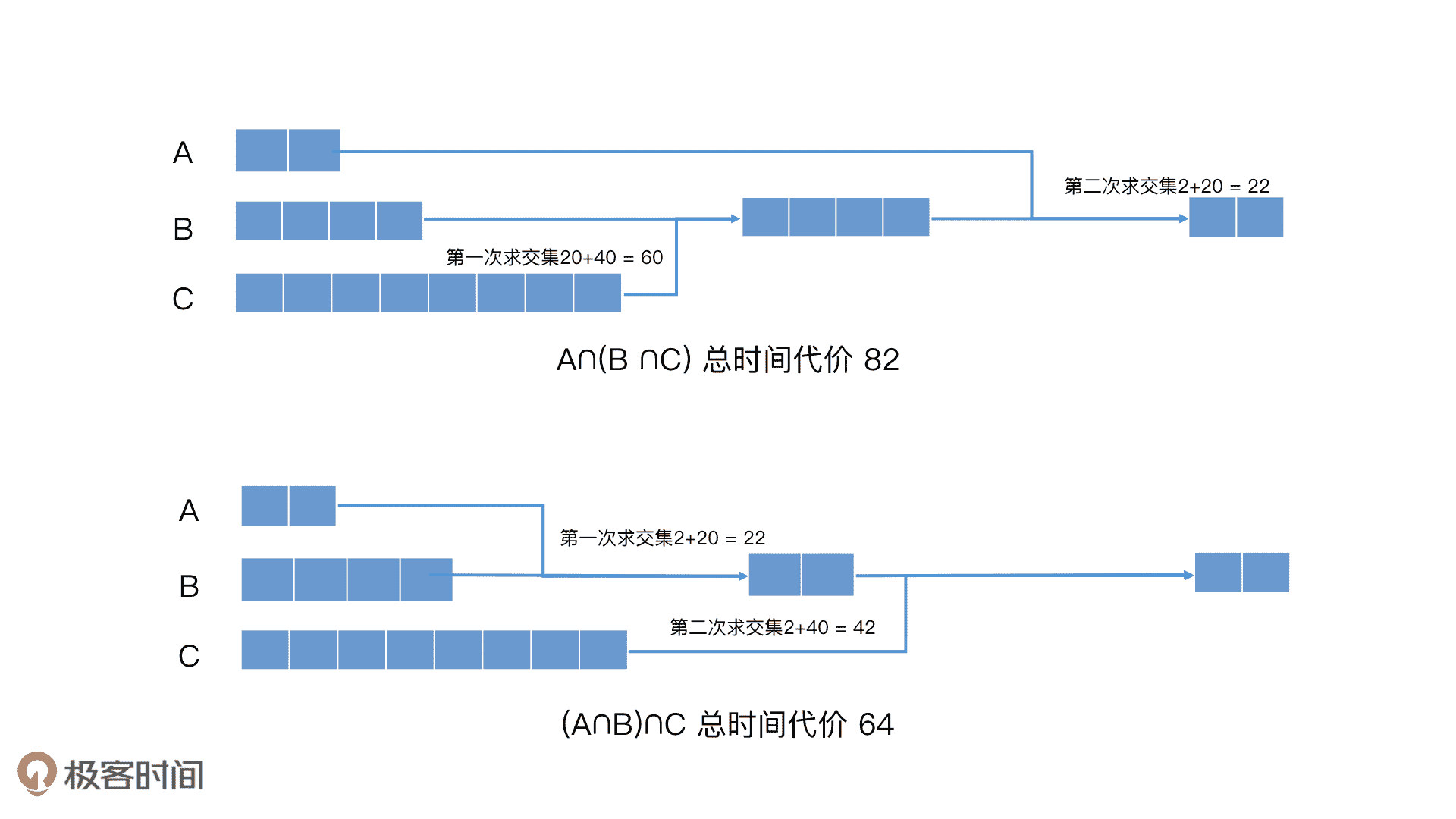
求 A∩(B∩C)和(A∩B)∩C 的过程
除了对 A、B、C 这三个集合同时取交集以外,还有一种常见的联合查询方式,就是对其中两个集合取并集之后,再和第三个集合取交集,比如 A ∩(B∪C),你可以看我开头举的第一个例子。在这种情况下,如果我们不做任何优化,查询代价是怎么样的呢?让我们一起来看一下。
首先是执行 B∪C 的操作,时间代价是 20 + 40 = 60,结果是 C。然后再和 A 求交集,时间代价是 2+40 = 42。一共是 102。
这样的时间代价非常大,那针对这个查询过程我们还可以怎么优化呢?这种情况下,我们可以尝试使用数学公式,对先求并集再求交集的次序进行改造,我们先来复习一个集合分配律公式:
A∩(B∪C)=(A∩B)∪(A∩C)
然后,我们就可以把先求并集再求交集的操作,转为先求交集再求并集的操作了。那这个时候,查询的时间代价是多少呢?我们一起来看一下。
首先,我们要执行 A∩B 操作,时间代价是 2+20 = 22,结果是 A。然后,我们执行 A∩C 操作,时间代价是 2+40=42,结果也是 A。最后,我们对两个 A 求并集,时间代价是 2+2=4。因此,最终总的时间代价是 22 + 42 + 4 = 68。这比没有优化前的 102 要低得多。

求 A∩(B∪C)和(A∩B)∪(A∩C)的过程
这里有一点需要特别注意,如果求并集的元素很多,比如说(B∪C∪D∪E∪F),那我们用分配律改写的时候,A 就需要分别和 B 到 F 求 5 次交集,再将 5 个结果求并集。这样一来,操作的次数会多很多,性能就有可能下降。因此,我们需要先检查 B 到 F 每个集合的大小,比如说,如果集合中元素个数都明显大于 A,我们预测它们分别和 A 求交集能有提速的效果,那我们就可以使用集合分配律公式来加速检索。
不知道你有没有注意到,在一开始讲这两个例子的时候,我们假设了 A、B、C有相互包含的关系,这是为了方便你更好地理解调整操作次序带来的效率差异。那在真实情况中,集合中的关系不会这么理想,但是我们分析得到的结论,依然是有效的。
方法二:快速多路归并法
**但是,**调整次序法有一个前提,就是集合的大小要有一定的差异,这样的调整效果才会更明显。那如果我们要对多个 posting list 求交集,但是它们的长度差异并不大,这又该如何优化呢?这个时候,我们可以使用跳表法来优化。
在对多个 posting list 求交集的过程中,我们可以**利用跳表的性质,快速跳过多个元素,加快多路归并的效率。**这种方法,我叫它"快速多路归并法"。在一些搜索引擎和广告引擎中,包括在 Elastic Search 这类框架里,就都使用了这样的技术。那具体是怎么做的呢?我们一起来看一下。
其实,快速多路归并法的思路和实现都非常简单,就是将 n 个链表的当前元素看作一个有序循环数组list[n]。并且,对有序循环数组从小到大依次处理,当有序循环数组中的最小值等于最大值,也就是所有元素都相等时,就说明我们找到了公共元素。
这么说可能比较抽象,下面,我们就以 4 个链表 A、B、C、D 求交集为例,来讲一讲具体的实现步骤。
第 1 步,将 4 个链表的当前第一个元素取出,让它们按照由小到大的顺序进行排序。然后,将链表也按照由小到大有序排列;
第 2 步,用一个变量 max 记录当前 4 个链表头中最大的一个元素的值;
第 3 步,从第一个链表开始,判断当前位置的值是否和 max 相等。如果等于 max,则说明此时所有链表的当前元素都相等,该元素为公共元素,那我们就将该元素取出,然后回到第一步;如果当前位置的值小于 max,则用跳表法快速调整到该链表中第一个大于等于 max 的元素位置;如果新位置元素的值大于 max,则更新 max 的值。
第 4 步,对下一个链表重复第 3 步,就这样依次处理每个链表(处理完第四个链表后循环回到第一个链表,用循环数组实现),直到链表全部遍历完。
为了帮助你加深理解,我在下面的过程图中加了一个具体的例子,你可以对照前面的文字描述一起消化吸收。
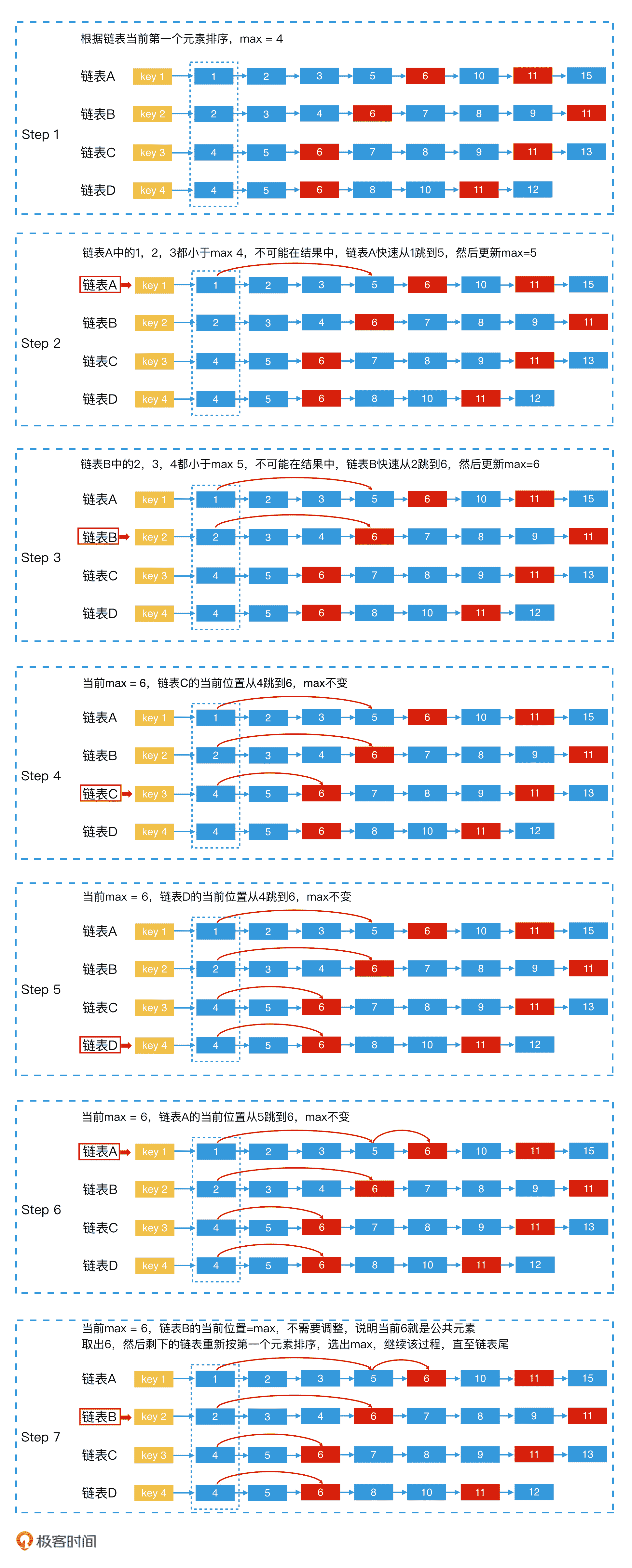
上图的例子中,我们通过以上 4 个步骤,找到了公共元素 6。接下来,你可以试着继续用这个方法,去找下一个公共元素 11。这里,我就不再继续举例了。
方法三:预先组合法
接下来,我们来说一说第三种方法,预先组合法。其实预先组合法的核心原理,和我们熟悉的一个系统实现理念一样,就是能提前计算好的,就不要临时计算。换一句话说,对于常见的联合查询,我们可以提前将结果算好,并将该联合查询定义一个 key。那具体该怎么操作呢?
假设,key1、key2 和 key3 分别的查询结果是 A、B、C 三个集合。如果我们经常会计算 A∩B∩C,那我们就可以将 key1+key2+key3 这个查询定义为一个新的组合 key,然后对应的 posting list 就是提前计算好的结果。之后,当我们要计算 A∩B∩C 时,直接去查询这个组合 key,取出对应的 posting list 就可以了。
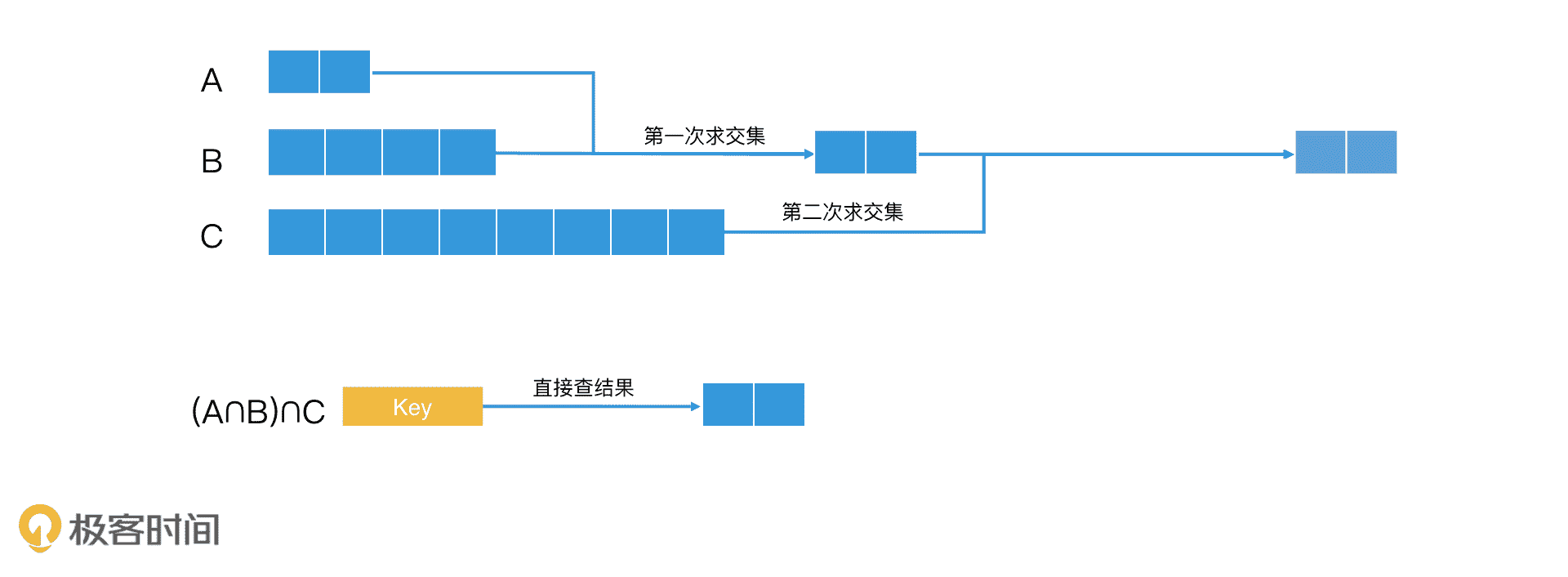
直接提前组合计算
方法四:缓存法加速联合查询
预先组合的方法非常实用,但是在搜索引擎以及一些具有热搜功能的平台中,经常会出现一些最新的查询组合。这些查询组合请求量也很大,但是由于之前没有出现过,因此我们无法使用预先组合的方案来优化。这个时候,我们会使用缓存技术来优化。
那什么是缓存技术呢?缓存技术就是指将之前的联合查询结果保存下来。这样再出现同样的查询时,我们就不需要重复计算了,而是直接取出之前缓存的结果即可。这里,我们可以借助预先组合法的优化思路,为每一个联合查询定义一个新的 key,将结果作为这个 key 的 posting list 保存下来。
但是,我们还要考虑一个问题:内存空间是有限的,不可能无限缓存所有出现过的查询组合。因此,对于缓存,我们需要进行内容替换管理。一种常用的缓存管理技术是 LRU(Least Recently Used),也叫作最近最少使用替换机制。所谓最近最少使用替换机制,就是如果一个对象长期未被访问,那当缓存满时,它将会被替换。
对于最近最少使用替换机制,一个合适的实现方案是使用双向链表:当一个元素被访问时,将它提到链表头。这个简单的机制能起到的效果是:如果一个元素经常被访问,它就会经常被往前提;如果一个元素长时间未被访问,它渐渐就会被排到链表尾。这样一来,当缓存满时,我们直接删除链表尾的元素即可。
不过,我们希望能快速查询缓存,那链表的访问速度就不满足我们的需求了。因此,我们可以使用 O(1) 查询代价的哈希表来优化。我们向链表中插入元素时,同时向哈希表中插入该元素的 key,然后这个 key 对应的 value 则是链表中这个节点的地址。这样,我们在查询这个 key 的时候,就可以通过查询哈希表,快速找到链表中的对应节点了。因此,使用“双向链表 + 哈希表”是一种常见的实现 LRU 机制的方案。

使用双向链表 + 哈希表实现 LRU 机制
通过使用 LRU 缓存机制,我们就可以将临时的查询组合缓存起来,快速查询出结果,而不需要重复计算了。一旦这个查询组合不是热点了,那它就会被 LRU 机制替换出缓存区,让位给新的热点查询组合。
缓存法在许多高并发的查询场景中,会起到相当大的作用。比如说在搜索引擎中,对于一些特定时段的热门查询,缓存命中率能达到 60% 以上甚至更高,会大大加速系统的检索效率。
重点回顾
好了,今天的内容就讲到这里。今天我们学习了联合查询的 4 种优化方法,我们一起来回顾一下。
第 1 种方法是调整次序法,它是通过从小到大求交集,以及使用集合分配律改写查询,使得检索效率得到提升。
第 2 种方法是快速多路归并法,它是利用跳表快速跳过多个元素的能力,结合优化的多路归并方案,提升多个 posting list 归并性能的。
第 3 种方法是预先组合法,也就是将热门的查询组合提前处理好,作为一个单独的 key,保存提前计算好的 posting list。
第 4 种则是使用缓存法,将临时的热点查询组合进行结果缓存处理,避免重复查询每次都要重复计算。
你会看到,这 4 种方法分别从数学、算法、线下工程和线上工程,这四种不同的方向对联合查询进行了优化。同时使用它们,能让我们从多个维度对联合查询进行加速。
通过上一篇加餐,我相信你也体会到了,如果我们能合理组合和灵活应用简单的数据结构和算法,就能构建出复杂的架构,让它们在工业界的大规模系统中发挥重要的作用。那通过这一篇加餐,你还可以体会到,基础知识的全面性能帮助你从不同的维度去思考,教你用更多的手段去优化系统。
因此,在学习的金字塔中,扎实和稳健的基础知识永远是最重要。多花点时间,打好基础,我相信你一定会有巨大的收获!
课堂讨论
最后,我们还是来看一道讨论题。
对于今天介绍的四种方案,你觉得哪一种给你的印象最深刻?你会尝试在怎么样的场景中使用它?为什么?
欢迎在留言区畅所欲言,说出你的思考过程和答案。如果有收获,也欢迎把这篇文章分享给你的朋友。
文章作者 anonymous
上次更新 2024-01-23