04|状态检索:如何快速判断一个用户是否存在?
文章目录
你好,我是陈东。
在实际工作中,我们经常需要判断一个对象是否存在。比如说,在注册新用户时,我们需要先快速判断这个用户 ID 是否被注册过;再比如说,在爬虫系统抓取网页之前,我们要判断一个 URL 是否已经被抓取过,从而避免无谓的、重复的抓取工作。
那么,对于这一类是否存在的状态检索需求,如果直接使用我们之前学习过的检索技术,有序数组、二叉检索树以及哈希表来实现的话,它们的检索性能如何呢?是否还有优化的方案呢?今天,我们就一起来讨论一下这些问题。
如何使用数组的随机访问特性提高查询效率?
以注册新用户时查询用户 ID 是否存在为例,我们可以直接使用有序数组、二叉检索树或者哈希表来存储所有的用户 ID。
我们知道,无论是有序数组还是二叉检索树,它们都是使用二分查找的思想从中间元素开始查起的。所以,在查询用户 ID 是否存在时,它们的平均检索时间代价都是 O(log n),而哈希表的平均检索时间代价是 O(1)。因此,如果我们希望能快速查询出元素是否存在,那哈希表无疑是最合适的选择。不过,如果从工程实现的角度来看的话,哈希表的查询过程还是可以优化的。
比如说,如果我们要查询的对象 ID 本身是正整数类型,而且 ID 范围有上限的话。我们就可以申请一个足够大的数组,让数组的长度超过 ID 的上限。然后,把数组中所有位置的值都初始化为 0。对于存在的用户,我们直接将用户 ID 的值作为数组下标,将该位置的值从 0 设为 1 就可以了。
这种情况下,当我们查询一个用户 ID 是否存在时,会直接以该 ID 为数组下标去访问数组,如果该位置为 1,说明该 ID 存在;如果为 0,就说明该 ID 不存在。和哈希表的查找流程相比,这个流程就节省了计算哈希值得到数组下标的环节,并且直接利用数组随机访问的特性,在 O(1) 的时间内就能判断出元素是否存在,查询效率是最高的。
但是,直接使用 ID 作为数组下标会有一个问题:如果 ID 的范围比较广,比如说在 10 万之内,那我们就需要保证数组的长度大于 10 万。所以,这种方案的占用空间会很大。
而且,如果这个数组是一个 int 32 类型的整型数组,那么每个元素就会占据 4 个字节,用 4 个字节来存储 0 和 1 会是一个巨大的空间浪费。那我们该如何优化呢?你可以先想一想,然后我们一起来讨论。
如何使用位图来减少存储空间?
最直观的一个想法就是,使用最少字节的类型来定义数组。比如说,使用 1 个字节的 char 类型数组,或者使用 bool 类型的数组(在许多系统中,一个 bool 类型的元素也是 1 个字节)。它们和 4 个字节的 int 32 数组相比,空间使用效率提升了 4 倍,这已经算是不错的改善了。
但是,使用 char 类型的数组,依然是一个非常“浪费空间”的方案。因为表示 0 或者 1,理论上只需要一个 bit。所以,如果我们能以 bit 为单位来构建这个数组,那使用空间就是 int 32 数组的 1/32,从而大幅减少了存储使用的内存空间。这种以 bit 为单位构建数组的方案,就叫作 Bitmap,翻译为位图。
位图的优势非常明显,但许多系统中并没有以 bit 为单位的数据类型。因此,我们往往需要对其他类型的数组进行一些转换设计,使其能对相应的 bit 位的位置进行访问,从而实现位图。
我们以 char 类型的数组为例子。假设我们申请了一个 1000 个元素的 char 类型数组,每个 char 元素有 8 个 bit,如果一个 bit 表示一个用户,那么 1000 个元素的 char 类型数组就能表示 8*1000 = 8000 个用户。如果一个用户的 ID 是 11,那么位图中的第 11 个 bit 就表示这个用户是否存在的信息。
这种情况下,我们怎么才能快速访问到第 11 个 bit 呢?
首先,数组是以 char 类型的元素为一个单位的,因此,我们的第一步,就是要找到第 11 个 bit 在数组的第几个元素里。具体的计算过程:一个元素占 8 个 bit,我们用 11 除以 8,得到的结果是 1,余数是 3。这就代表着,第 11 个 bit 存在于第 2 个元素里,并且在第 2 个元素里的位置是第 3 个。
对于第 2 个元素的访问,我们直接使用数组下标 [1] 就可以在 O(1) 的时间内访问到。对于第 2 个元素中的第 3 个 bit 的访问,我们可以通过位运算,先构造一个二进制为 00100000 的字节(字节的第 3 位为 1),然后和第 2 个元素做 and 运算,就能得知该元素的第 3 位是 1 还是 0。这也是一个时间代价为 O(1) 的操作。这样一来,通过两次 O(1) 时间代价的查找,我们就可以知道第 11 个 bit 的值是 0 还是 1 了。

用户 ID 为 11 的位图定位
尽管位图相对于原始数组来说,在元素存储上已经有了很大的优化,但如果我们还想进一步优化存储空间,是否还有其他的优化方案呢?我们知道,一个数组所占的空间其实就是“数组元素个数 * 每个元素大小”。我们已经将每个元素大小压缩到了最小单位 1 个 bit,如果还要进行优化,那么自然会想到优化“数组元素个数”。
没错,限制数组的长度是一个可行的方案。不过前面我们也说了,数组长度必须大于 ID 的上限。因此,如果我们希望将数组长度压缩到一个足够小的值之内,我们就需要使用哈希函数将大于数组长度的用户 ID,转换为一个小于数组长度的数值作为下标。除此以外,使用哈希函数也带来了另一个优点,那就是我们不需要把用户 ID 限制为正整数了,它也可以是字符串。这样一来,压缩数组长度,并使用哈希函数,就是一个更加通用的解决方案。
但是我们也知道,数组压缩得越小,发生哈希冲突的可能性就会越大,如果两个元素 A 和 B 的哈希值冲突了,映射到了同一个位置。那么,如果我们查询 A 时,该位置的结果为 1,其实并不能说明元素 A 一定存在。因此,如何在数组压缩的情况下缓解哈希冲突,保证一定的查询正确率,是我们面临的主要问题。
在第 3 讲中,我们讲了哈希表解决哈希冲突的两种常用方法:开放寻址法和链表法。开放寻址法中有一个优化方案叫“双散列”,它的原理是使用多个哈希函数来解决冲突问题。我们能否借鉴这个思想,在位图的场景下使用多个哈希函数来降低冲突概率呢?没错,这其实就是布隆过滤器(Bloom Filter)的设计思想。
布隆过滤器最大的特点,就是对一个对象使用多个哈希函数。如果我们使用了 k 个哈希函数,就会得到 k 个哈希值,也就是 k 个下标,我们会把数组中对应下标位置的值都置为 1。布隆过滤器和位图最大的区别就在于,我们不再使用一位来表示一个对象,而是使用 k 位来表示一个对象。这样两个对象的 k 位都相同的概率就会大大降低,从而能够解决哈希冲突的问题了。
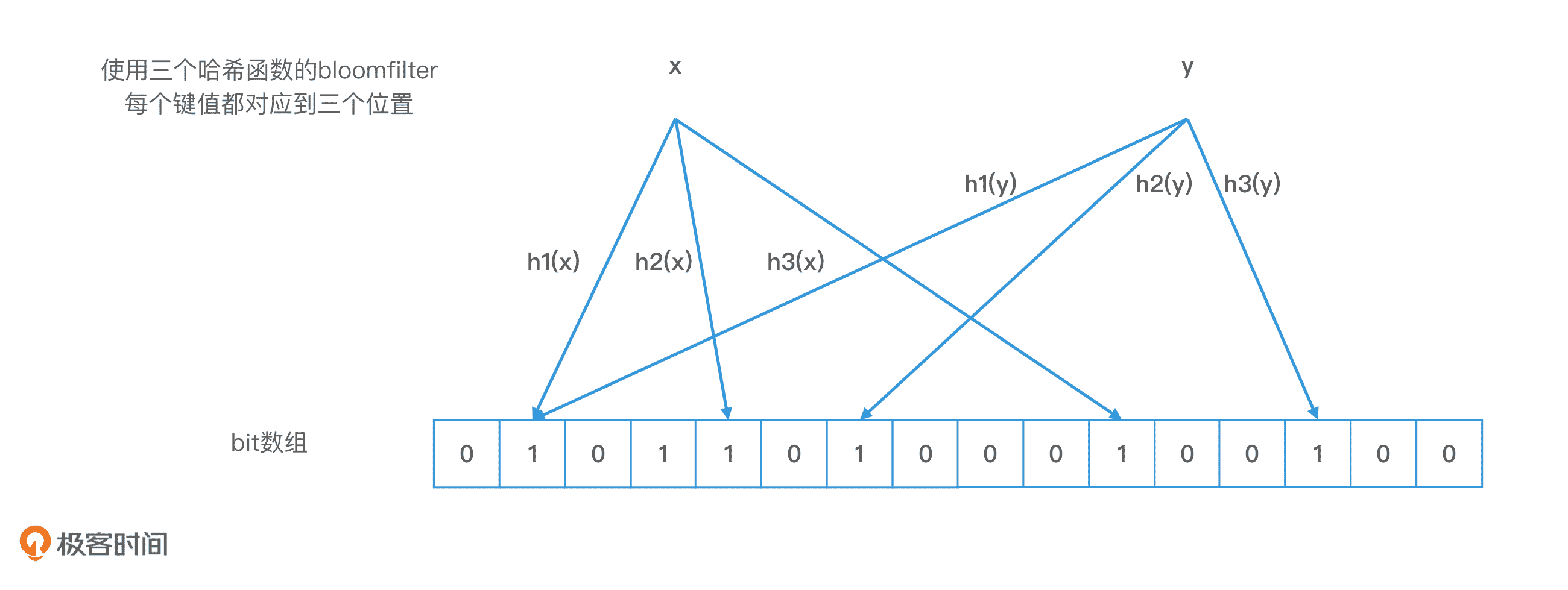
Bloom filter 示例
但是,布隆过滤器的查询有一个特点,就是即使任何两个元素的哈希值不冲突,而且我们查询对象的 k 个位置的值都是 1,查询结果为存在,这个结果也可能是错误的。这就叫作布隆过滤器的错误率。
我在下图给出了一个例子。我们可以看到,布隆过滤器中存储了 x 和 y 两个对象,它们对应的 bit 位被置为 1。当我们查询一个不存在的对象 z 时,如果 z 的 k 个哈希值的对应位置的值正好都是 1,z 就会被错误地认定为存在。而且,这个时候,z 和 x,以及 z 和 y,两两之间也并没有发生哈希冲突。

Bloom filter 错误率示例
那遇到“可能存在”这样的情况,我们该怎么办呢?不要忘了我们的使用场景:我们希望用更小的代价快速判断 ID 是否已经被注册了。在这个使用场景中,就算我们无法确认 ID 是否已经被注册了,让用户再换一个 ID 注册,这也不会损害新用户的体验。在系统不要求结果 100% 准确的情况下,我们可以直接当作这个用户 ID 已经被注册了就可以了。这样,我们使用布隆过滤器就可以快速完成“是否存在”的检索。
除此之外,对于布隆过滤器而言,如果哈希函数的个数不合理,比如哈希函数特别多,布隆过滤器的错误率就会变大。因此,除了使用多个哈希函数避免哈希冲突以外,我们还要控制布隆过滤器中哈希函数的个数。有这样一个计算最优哈希函数个数的数学公式:哈希函数个数 k = (m/n) * ln(2)。其中 m 为 bit 数组长度,n 为要存入的对象的个数。实际上,如果哈希函数个数为 1,且数组长度足够,布隆过滤器就可以退化成一个位图。所以,我们可以认为“位图是只有一个特殊的哈希函数,且没有被压缩长度的布隆过滤器”。
重点回顾
好了,状态检索的内容我们就讲到这里。我们一起来总结一下,这一讲你要掌握的重点内容。
今天,我们主要解决了快速判断一个对象是否存在的问题。相比于有序数组、二叉检索树和哈希表这三种方案,位图和布隆过滤器其实更适合解决这类状态检索的问题。这是因为,在不要求 100% 判断正确的情况下,使用位图和布隆过滤器可以达到 O(1) 时间代价的检索效率,同时空间使用率也非常高效。
虽然位图和布隆过滤器的原理和实现都非常简单,但是在许多复杂的大型系统中都可以见到它们的身影。
比如,存储系统中的数据是存储在磁盘中的,而磁盘中的检索效率非常低,因此,我们往往会先使用内存中的布隆过滤器来快速判断数据是否存在,不存在就直接返回,只有可能存在才会去磁盘检索,这样就避免了为无效数据读取磁盘的额外开销。
再比如,在搜索引擎中,我们也需要使用布隆过滤器快速判断网站是否已经被抓取过,如果一定不存在,我们就直接去抓取;如果可能存在,那我们可以根据需要,直接放弃抓取或者再次确认是否需要抓取。你会发现,这种快速预判断的思想,也是提高应用整体检索性能的一种常见设计思路。
课堂讨论
这节课的内容,你可以结合这道讨论题进一步加深理解:
如果位图中一个元素被删除了,我们可以将对应 bit 位置为 0。但如果布隆过滤器中一个元素被删除了,我们直接将对应的 k 个 bit 位置为 0,会产生什么样的问题呢?为什么?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这篇文章分享给你的朋友。
文章作者 anonymous
上次更新 2024-01-23