07|NoSQL检索:为什么日志系统主要用LSM树而非B+树?
文章目录
你好,我是陈东。
B+ 树作为检索引擎中的核心技术得到了广泛的使用,尤其是在关系型数据库中。
但是,在关系型数据库之外,还有许多常见的大数据应用场景,比如,日志系统、监控系统。这些应用场景有一个共同的特点,那就是数据会持续地大量生成,而且相比于检索操作,它们的写入操作会非常频繁。另外,即使是检索操作,往往也不是全范围的随机检索,更多的是针对近期数据的检索。
那对于这些应用场景来说,使用关系型数据库中的 B+ 树是否合适呢?
我们知道,B+ 树的数据都存储在叶子节点中,而叶子节点一般都存储在磁盘中。因此,每次插入的新数据都需要随机写入磁盘,而随机写入的性能非常慢。如果是一个日志系统,每秒钟要写入上千条甚至上万条数据,这样的磁盘操作代价会使得系统性能急剧下降,甚至无法使用。
那么,针对这种频繁写入的场景,是否有更合适的存储结构和检索技术呢?今天,我们就来聊一聊另一种常见的设计思路和检索技术:LSM 树(Log Structured Merge Trees)。LSM 树也是近年来许多火热的 NoSQL 数据库中使用的检索技术。
如何利用批量写入代替多次随机写入?
刚才我们提到 B+ 树随机写入慢的问题,对于这个问题,我们现在来思考一下优化想法。操作系统对磁盘的读写是以块为单位的,我们能否以块为单位写入,而不是每次插入一个数据都要随机写入磁盘呢?这样是不是就可以大幅度减少写入操作了呢?
LSM 树就是根据这个思路设计了这样一个机制:当数据写入时,延迟写磁盘,将数据先存放在内存中的树里,进行常规的存储和查询。当内存中的树持续变大达到阈值时,再批量地以块为单位写入磁盘的树中。因此,LSM 树至少需要由两棵树组成,一棵是存储在内存中较小的 C0 树,另一棵是存储在磁盘中较大的 C1 树。简单起见,接下来我们就假设只有 C0 树和 C1 树。

LSM 树由至少 2 部分组成:内存的 C0 树和磁盘的 C1 树
C1 树存储在磁盘中,因此我们可以直接使用 B+ 树来生成。那对于全部存储在内存中的 C0 树,我们该如何生成呢?在上一讲的重点回顾中我们分析过,在数据都能加载在内存中的时候,B+ 树并不是最合适的选择,它的效率并不会更高。因此,C0 树我们可以选择其他的数据结构来实现,比如平衡二叉树甚至跳表等。但是为了让你更简单、清晰地理解 LSM 树的核心理念,我们可以假设 C0 树也是一棵 B+ 树。
那现在 C0 树和 C1 树就都是 B+ 树生成的了,但是相比于普通 B+ 树生成的 C0 树,C1 树有一个特点:所有的叶子节点都是满的。为什么会这样呢?原因就是,C1 树不需要支持随机写入了,我们完全可以等内存中的数据写满一个叶子节点之后,再批量写入磁盘。因此,每个叶子节点都是满的,不需要预留空位来支持新数据的随机写入。
如何保证批量写之前系统崩溃可以恢复?
B+ 树随机写入慢的问题,我们已经知道解决的方案了。现在第二个问题来了:如果机器断电或系统崩溃了,那内存中还未写入磁盘的数据岂不就永远丢失了?这种情况我们该如何解决呢?
为了保证内存中的数据在系统崩溃后能恢复,工业界会使用 WAL 技术(Write Ahead Log,预写日志技术)将数据第一时间高效写入磁盘进行备份。WAL 技术保存和恢复数据的具体步骤,我这里总结了一下。
- 内存中的程序在处理数据时,会先将对数据的修改作为一条记录,顺序写入磁盘的 log 文件作为备份。由于磁盘文件的顺序追加写入效率很高,因此许多应用场景都可以接受这种备份处理。
- 在数据写入 log 文件后,备份就成功了。接下来,该数据就可以长期驻留在内存中了。
- 系统会周期性地检查内存中的数据是否都被处理完了(比如,被删除或者写入磁盘),并且生成对应的检查点(Check Point)记录在磁盘中。然后,我们就可以随时删除被处理完的数据了。这样一来,log 文件就不会无限增长了。
- 系统崩溃重启,我们只需要从磁盘中读取检查点,就能知道最后一次成功处理的数据在 log 文件中的位置。接下来,我们就可以把这个位置之后未被处理的数据,从 log 文件中读出,然后重新加载到内存中。
通过这种预先将数据写入 log 文件备份,并在处理完成后生成检查点的机制,我们就可以安心地使用内存来存储和检索数据了。
如何将内存数据与磁盘数据合并?
解决了内存中数据备份的问题,我们就可以接着写入数据了。内存中 C0 树的大小是有上限的,那当 C0 树被写满之后,我们要怎么把它转换到磁盘中的 C1 树上呢?这就涉及滚动合并(Rolling Merge)的过程了。
我们可以参考两个有序链表归并排序的过程,将 C0 树和 C1 树的所有叶子节点中存储的数据,看作是两个有序链表,那滚动合并问题就变成了我们熟悉的两个有序链表的归并问题。不过由于涉及磁盘操作,那为了提高写入效率和检索效率,我们还需要针对磁盘的特性,在一些归并细节上进行优化。
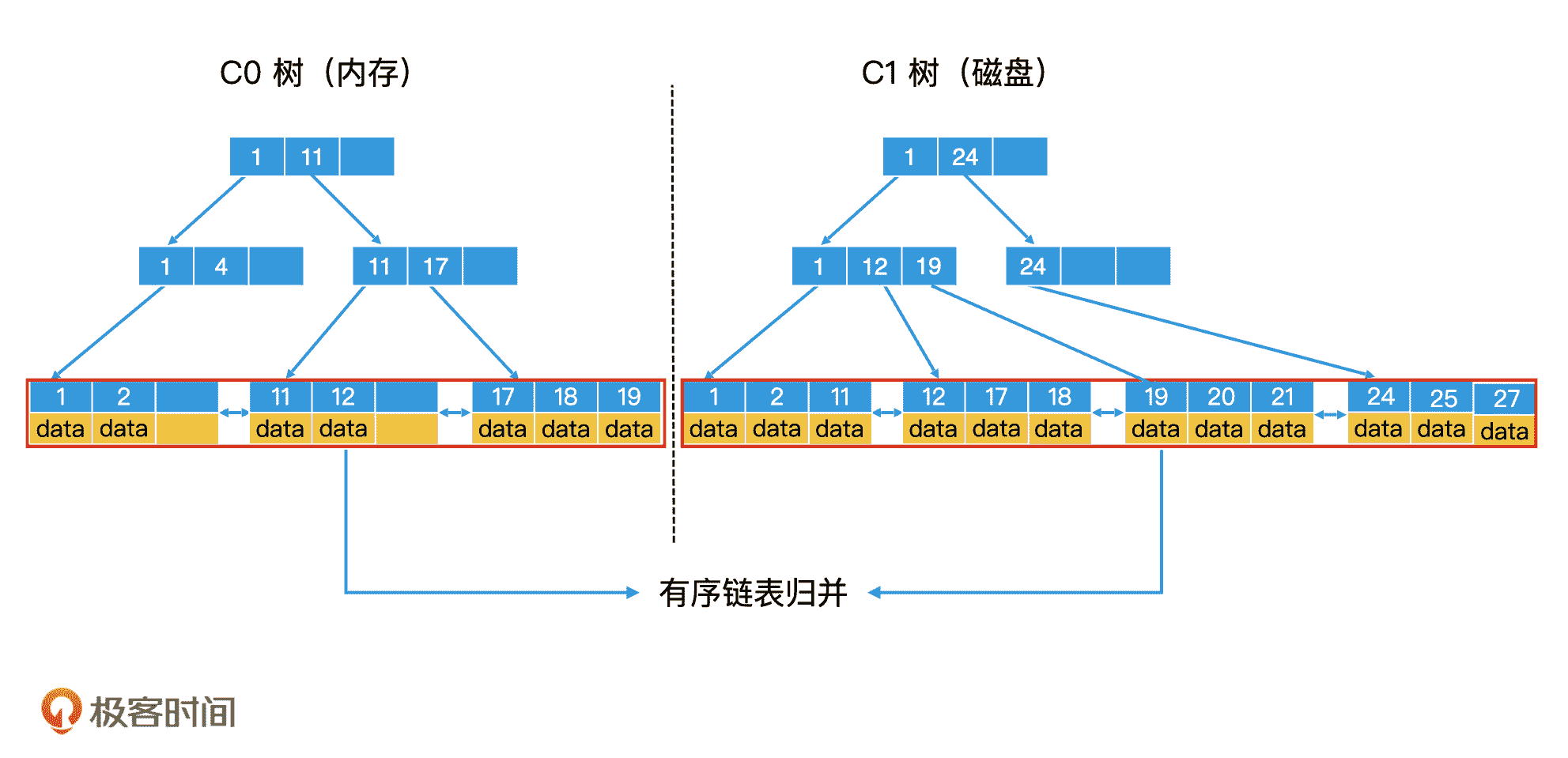
C0 树和 C1 树滚动合并可以视为有序链表归并
由于磁盘具有顺序读写效率高的特性,因此,为了提高 C1 树中节点的读写性能,除了根节点以外的节点都要尽可能地存放到连续的块中,让它们能作为一个整体单位来读写。这种包含多个节点的块就叫作多页块(Multi-Pages Block)。
下面,我们来讲一下滚动归并的过程。在进行滚动归并的时候,系统会遵循以下几个步骤。
第一步,以多页块为单位,将 C1 树的当前叶子节点从前往后读入内存。读入内存的多页块,叫作清空块(Emptying Block),意思是处理完以后会被清空。
第二步,将 C0 树的叶子节点和清空块中的数据进行归并排序,把归并的结果写入内存的一个新块中,叫作填充块(Filling Block)。
第三步,如果填充块写满了,我们就要将填充块作为新的叶节点集合顺序写入磁盘。这个时候,如果 C0 树的叶子节点和清空块都没有遍历完,我们就继续遍历归并,将数据写入新的填充块。如果清空块遍历完了,我们就去 C1 树中顺序读取新的多页块,加载到清空块中。
第四步,重复第三步,直到遍历完 C0 树和 C1 树的所有叶子节点,并将所有的归并结果写入到磁盘。这个时候,我们就可以同时删除 C0 树和 C1 树中被处理过的叶子节点。这样就完成了滚动归并的过程。

使用清空块和填充块进行滚动归并
在 C0 树到 C1 树的滚动归并过程中,你会看到,几乎所有的读写操作都是以多页块为单位,将多个叶子节点进行顺序读写的。而且,因为磁盘的顺序读写性能和内存是一个数量级的,这使得 LSM 树的性能得到了大幅的提升。
LSM 树是如何检索的?
现在你已经知道 LSM 树的组织过程了,我们可以来看,LSM 树是如何完成检索的。
因为同时存在 C0 和 C1 树,所以要查询一个 key 时,我们会先到 C0 树中查询。如果查询到了则直接返回,不用再去查询 C1 树了。
而且,C0 树会存储最新的一批数据,所以 C0 树中的数据一定会比 C1 树中的新。因此,如果一个系统的检索主要是针对近期数据的,那么大部分数据我们都能在内存中查到,检索效率就会非常高。
那如果我们在 C0 树中没有查询到 key 呢?这个时候,系统就会去磁盘中的 C1 树查询。在 C1 树中查到了,我们能直接返回吗?如果没有特殊处理的话,其实并不能。你可以先想想,这是为什么。
我们先来考虑一种情况:一个数据已经被写入系统了,并且我们也把它写入 C1 树了。但是,在最新的操作中,这个数据被删除了,那我们自然不会在 C0 树中查询到这个数据。可是它依然存在于 C1 树之中。
这种情况下,我们在 C1 树中检索到的就是过期的数据。既然是过期的数据,那为了不影响检索结果,我们能否从 C1 树中将这个数据删除呢?删除的思路没有错,但是不要忘了,我们不希望对 C1 树进行随机访问。这个时候,我们又该怎么处理呢?
我们依然可以采取延迟写入和批量操作的思路。对于被删除的数据,我们会将这些数据的 key 插入到 C0 树中,并且存入删除标志。如果 C0 树中已经存有这些数据,我们就将 C0 树中这些数据对应的 key 都加上删除标志。
这样一来,当我们在 C0 树中查询时,如果查到了一个带着删除标志的 key,就直接返回查询失败,我们也就不用去查询 C1 树了。在滚动归并的时候,我们会查看数据在 C0 树中是否带有删除标志。如果有,滚动归并时就将它放弃。这样 C1 树就能批量完成“数据删除”的动作。
重点回顾
好了,今天的内容就先讲到这里。我们一起来回顾一下,你要掌握的重点内容。
在写大于读的应用场景下,尤其是在日志系统和监控系统这类应用中,我们可以选用基于 LSM 树的 NoSQL 数据库,这是比 B+ 树更合适的技术方案。
LSM 树具有以下 3 个特点:
- 将索引分为内存和磁盘两部分,并在内存达到阈值时启动树合并(Merge Trees);
- 用批量写入代替随机写入,并且用预写日志 WAL 技术保证内存数据,在系统崩溃后可以被恢复;
- 数据采取类似日志追加写的方式写入(Log Structured)磁盘,以顺序写的方式提高写入效率。
LSM 树的这些特点,使得它相对于 B+ 树,在写入性能上有大幅提升。所以,许多 NoSQL 系统都使用 LSM 树作为检索引擎,而且还对 LSM 树进行了优化以提升检索性能。在后面的章节中我们会介绍,工业界中实际使用的 LSM 树是如何实现的,帮助你对 LSM 树有更深入的认识。
课堂讨论
为了方便你理解,文章中我直接用 B+ 树实现的 C0 树。但是,对于纯内存操作,其他的类树结构会更合适。如果让你来设计的话,你会采用怎么样的结构作为 C0 树呢?
欢迎在留言区畅所欲言,说出你的思考过程和最终答案。如果有收获,也欢迎把这篇文章分享给你的朋友。
文章作者 anonymous
上次更新 2024-01-23