11|精准TopK检索:搜索结果是怎么进行打分排序的?
文章目录
你好,我是陈东。
在搜索引擎的检索结果中,排在前面几页的检索结果往往质量更好,更符合我们的要求。一般来说,这些高质量检索结果的排名越靠前,这个搜索引擎的用户体验也就越好。可以说,检索结果的排序是否合理,往往决定了一个检索系统的质量。
所以,在搜索引擎这样的大规模检索系统中,排序是非常核心的一个环节。简单来说,排序就是搜索引擎对符合用户要求的检索结果进行打分,选出得分最高的 K 个检索结果的过程。这个过程也叫作 Top K 检索。
今天,我就和你仔细来聊一聊,搜索引擎在 Top K 检索中,是如何进行打分排序的。
经典的 TF-IDF 算法是什么?
在搜索引擎的应用场景中,检索结果文档和用户输入的查询词之间的相关性越强,网页排名就越靠前。所以,在搜索引擎对检索结果的打分中,查询词和结果文档的相关性是一个非常重要的判断因子。
那要计算相关性,就必须要提到经典的 TF-IDF 算法了,它能很好地表示一个词在一个文档中的权重。TF-IDF 算法的公式是:相关性 = TF*IDF。其中,TF 是词频(Term Frequency),IDF 是逆文档频率(Inverse Document Frequency)。
在利用 TF-IDF 算法计算相关性之前,我们还要理解几个重要概念,分别是词频、文档频率和逆文档频率。
词频定义的就是一个词项在文档中出现的次数。换一句话说就是,如果一个词项出现了越多次,那这个词在文档中就越重要。
文档频率(Document Frequency),指的是这个词项出现在了多少个文档中。你也可以理解为,如果一个词出现在越多的文档中,那这个词就越普遍,越没有区分度。一个极端的例子,比如“的”字,它基本上在每个文档中都会出现,所以它的区分度就非常低。
那为了方便理解和计算相关性,我们又引入了一个逆文档频率的概念。逆文档频率是对文档频率取倒数,它的值越大,这个词的的区分度就越大。
因此,TF*IDF 表示了我们综合考虑了一个词项的重要性和区分度,结合这两个维度,我们就计算出了一个词项和文档的相关性。不过,在计算的过程中,我们会对 TF 和 IDF 的值都使用对数函数进行平滑处理。处理过程如下图所示:

使用“相关性 = TF*IDF”,我们可以计算一个词项在一个文档中的权重。但是,很多情况下,一个查询中会有多个词项。不过,这也不用担心,处理起来也很简单。我们直接把每个词项和文档的相关性累加起来,就能计算出查询词和文档的总相关性了。
这么说可能比较抽象,我列举了一些具体的数字,我们一起动手来计算一下相关性。假设查询词是“极客时间”,它被分成了两个词项“极客”和“时间”。现在有两个文档都包含了“极客”和“时间”,在文档 1 中,“极客”出现了 10 次,“时间”出现了 10 次。而在文档 2 中,“极客”出现了 1 次,“时间”出现了 100 次。
计算 TF-IDF 需要的数据如下表所示:

那两个文档的最终相关性得分如下:
文档 1 打分 =TF*IDF(极客)+ TF*IDF(时间)= (1+log(10)) * 10 + (1+log(10)) * 1 = 20 + 2 = 22
文档 2 打分 = TF*IDF(极客)+ TF*IDF(时间)=(1+log(1)) * 10 + (1+log(100)) * 1 = 10 + 3 = 13
你会发现,尽管“时间”这个词项在文档 2 中出现了非常多次,但是,由于“时间”这个词项的 IDF 值比较低,因此,文档 2 的打分并没有文档 1 高。
如何使用概率模型中的 BM25 算法进行打分?
不过,在实际使用中,我们往往不会直接使用 TF-IDF 来计算相关性,而是会以 TF-IDF 为基础,使用向量模型或者概率模型等更复杂的算法来打分。比如说,概率模型中的 BM25(Best Matching 25)算法,这个经典算法就可以看作是 TF-IDF 算法的一种升级。接下来,我们就一起来看看,BM25 算法是怎么打分的。
BM25 算法的一个重要的设计思想是,它认为词频和相关性的关系并不是线性的。也就是说,随着词频的增加,相关性的增加会越来越不明显,并且还会有一个阈值上限。当词频达到阈值以后,那相关性就不会再增长了。
因此,BM25 对于 TF 的使用,设立了一个公式,公式如下:

在这个公式中,随着 tf 的值逐步变大,权重会趋向于 k1 + 1 这个固定的阈值上限(将公式的分子分母同时除以 tf,就能看出这个上限)。其中,k1 是可以人工调整的参数。k1 越大,权重上限越大,收敛速度越慢,表示 tf 越重要。在极端情况下,也就是当 k1 = 0 时,就表示 tf 不重要。比如,在下图中,当 k1 = 3 就比 k1 = 1.2 时的权重上限要高很多。那按照经验来说,我们会把 k1 设为 1.2。
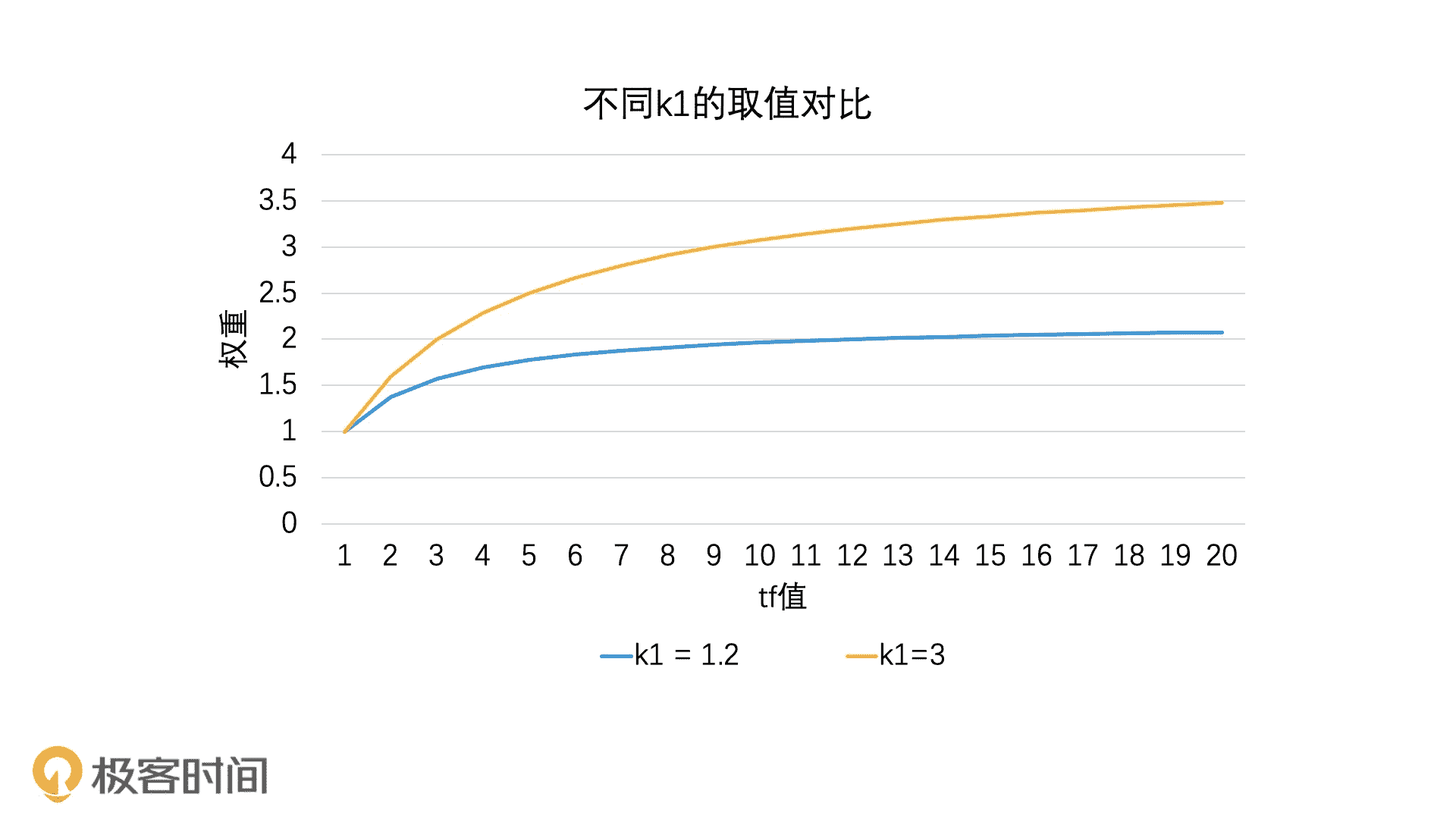
除了考虑词频,BM25 算法还考虑了文档长度的影响,也就是同样一个词项,如果在两篇文档中出现了相同的次数,但一篇文档比较长,而另一篇文档比较短,那一般来说,短文档中这个词项会更重要。这个时候,我们需要在上面的公式中,加入文档长度相关的因子。那么,整个公式就会被改造成如下的样子:

你会看到,分母中的 k1 部分被乘上了文档长度的权重。其中,l 表示当前文档的长度,而 L 表示全部文档的平均长度。l 越长,分母中的 k1 就会越大,整体的相关性权重就会越小。
这个公式中除了 k1,还有一个可以人工调整的参数 b。它的取值范围是 0 到 1,它 代表了文档长度的重要性。当 b 取 0 时,我们可以完全不考虑文档长度的影响;而当 b 取 1 时,k1 的重要性要按照文档长度进行等比例缩放。按照经验,我们会把 b 设置为 0.75,这样的计算效果会比较好。
除此以外,如果查询词比较复杂,比如说一个词项会重复出现,那我们也可以把它看作是一个短文档,用类似的方法计算词项在查询词中的权重。举个例子,如果我们的查询词是“极客们的极客时间课程”,那么“极客”这个词项,其实在查询词中就出现了两次,它的权重应该比“时间”“课程”这些只出现一次的词项更重要。因此,BM25 对词项在查询词中的权重计算公式如下:

其中 tfq表示词项在查询词 q 中的词频,而 k2 是可以人工调整的参数,它和 k1 的参数作用是类似的。由于查询词一般不会太长,所以词频也不会很大,因此,我们没必要像对待文档一下,用 k1 = 1.2 这么小的范围对它进行控制。我们可以放大词频的作用,把 k2 设置在 0~10 之间。极端情况下,也就是当 k2 取 0 时,表示我们可以完全不考虑查询词中的词项权重。
好了,前面我们说了这么多种权重公式,有基础的权重公式、文档中词项的权重公式和查询词中词项的权重公式。那在实际使用 BM25 算法打分的时候,我们该怎么使用这些公式呢?其实,我们可以回顾一下标准的 TF-IDF,把其中的 TF 进行扩展,变为“文档中词项权重”和“查询词中词项权重”的乘积。这样,我们就得到了 BM25 算法计算一个词项和指定文档相关性的打分公式,公式如下:

你会看到,它由 IDF、文档中词项权重以及查询词中词项权重这三部分共同组成。
如果一个查询词 q 中有多个词项 t,那我们就要把每一个词项 t 和文档 d 的相关性都计算出来,最后累加。这样,我们就得到了这个查询词 q 和文档 d 的相关性打分结果,我们用 score(q,d) 来表示,公式如下:

这就是完整的 BM25 算法的表达式了。尽管这个公式看起来比较复杂,但是经过我们刚才一步一步的拆解,你应该可以很好地理解它了,它其实就是对 TF-IDF 的算法中的 TF 做了更细致的处理而已。其实,BM25 中的 IDF 的部分,我们也还可以优化,比如,基于二值独立模型对它进行退化处理(这是另一个分析相关性的模型,这里就不具体展开说了)之后,我们就可以得到一个和 IDF 相似的优化表示,公式如下:

你可以将它视为 IDF 的变体,用来替换公式中原有的 IDF 部分。
总结来说,BM25 算法就是一个对查询词和文档的相关性进行打分的概率模型算法。BM25 算法考虑了四个因子,分别为 IDF、文档长度、文档中的词频以及查询词中的词频。并且,公式中还加入了 3 个可以人工调整大小的参数,分别是:k1、k2 和 b。
因此,BM25 算法的效果比 TF-IDF 更好,应用也更广泛。比如说,在 Lucene 和 Elastic Search 这些搜索框架,以及 Google 这类常见的搜索引擎中,就都支持 BM25 排序。不过要用好它,你需要结合我们今天讲的内容,更清楚地理解它的原理。这样才能根据不同的场景,去调整相应的参数,从而取得更好的效果。
如何使用机器学习来进行打分?
随着搜索引擎的越来越重视搜索结果的排序和效果,我们需要考虑的因子也越来越多。比如说,官方的网站是不是会比个人网页在打分上有更高的权重?用户的历史点击行为是否也是相关性的一个衡量指标?
在当前的主流搜索引擎中,用来打分的主要因子已经有几百种了。如果我们要将这么多的相关因子都考虑进来,再加入更多的参数,那 BM25 算法是无法满足我们的需求的。
这个时候,机器学习就可以派上用场了。利用机器学习打分是近些年来比较热门的研究领域,也是许多搜索引擎目前正在使用的打分机制。
那机器学习具体是怎么打分的呢?原理很简单,就是把不同的打分因子进行加权求和。比如说,有 n 个打分因子,分别为 x1到 xn,而每个因子都有不同的权重,我们记为 w1到 wn,那打分公式就是:
Score = w1* x1+ w2* x2+ w3* x3+ …… + wn* xn
那你可能会问了,公式中的权重要如何确定呢?这就需要我们利用训练数据,让机器学习在离线阶段,自动学出最合适的权重。这样,就避免了人工制定公式和权重的问题。
当然,这个打分公式是不能直接使用的,因为它的取值范围是负无穷到正无穷。这是一个跨度很广的范围,并不好衡量和比较相关性。一般来说,我们会使用 Sigmoid 函数对 score 进行处理,让它处于 (0,1) 范围内。
Sigmoid 函数的取值范围是(0,1),它的函数公式和图像如下所示:
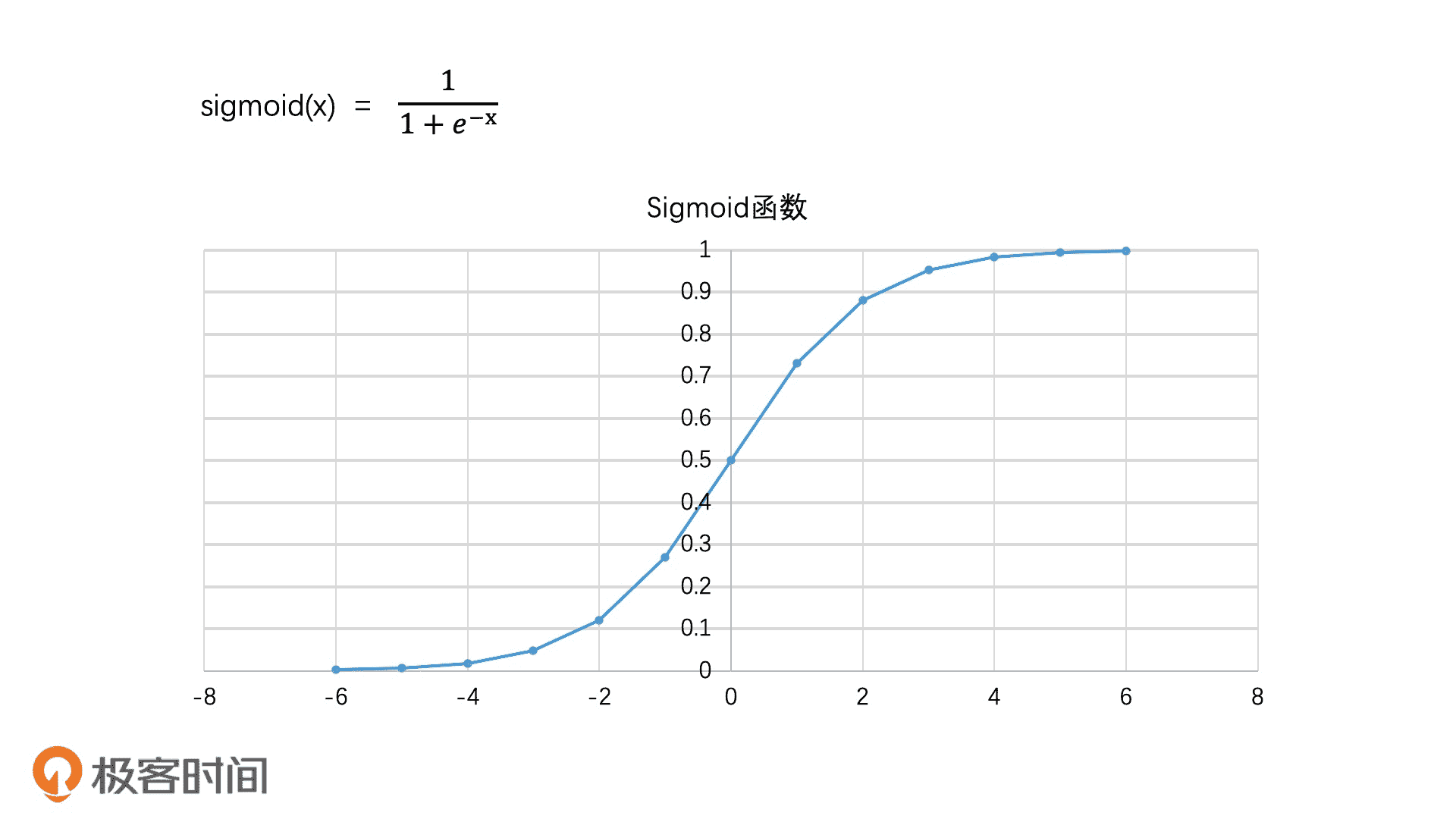
Sigmoid 函数图像(x 代表 score,y 代表相关性)
Sigmoid 函数的特点就是:x 值越大,y 值越接近于 1;x 值越小,y 值越接近于 0。并且,x 值在中间一段范围内,相关性的变化最明显,而在两头会发生边际效应递减的现象,这其实也符合我们的日常经验。比方说,一个 2-3 人的项目要赶进度,一开始增加 1、2 个人进来,项目进度会提升明显。但如果我们再持续加人进来,那项目的加速就会变平缓了。
这个打分方案,就是工业界常见的逻辑回归模型(Logistic Regression)(至于为什么逻辑回归模型的表现形式是 Sigmoid 函数,这是另一个话题,这里就不展开说了)。当然,工业界除了逻辑回归模型的打分方案,还有支持向量机模型、梯度下降树等。并且,随着深度学习的发展,也演化出了越来越多的复杂打分算法,比如,使用深度神经网络模型(DNN)和相关的变种等。由于机器学习和深度学习是专门的领域,因此相关的打分算法我就不展开了。在这一讲中,你只要记住,机器学习打分模型可以比人工规则打分的方式处理更多的因子,能更好地调整参数就可以了。
如何根据打分结果快速进行 Top K 检索?
在给所有的文档打完分以后,接下来,我们就要完成排序的工作了。一般来说,我们可以使用任意一种高效的排序算法来完成排序,比如说,我们可以使用快速排序,它排序的时间代价是 O(n log n)。但是,我们还要考虑到,搜索引擎检索出来结果的数量级可能是千万级别的。在这种情况下,即便是 O(n log n) 的时间代价,也会是一个非常巨大的时间损耗。
那对于这个问题,我们该怎么优化呢?
其实,你可以回想一下,我们在使用搜索引擎的时候,一般都不会翻超过 100 页(如果有兴趣,你可以试着翻翻,看 100 页以后搜索引擎会显示什么),而且,平均一页只显示 10 条数据。也就是说,搜索引擎其实只需要显示前 1000 条数据就够了。因此,在实际系统中,我们不需要返回所有结果,只需要返回 Top K 个结果就可以。这就是许多大规模检索系统应用的的 Top K 检索了。而且,我们前面的打分过程都是非常精准的,所以我们今天学习的也叫作精准 Top K 检索。
当然还有非精准的 Top K 检索,这里先卖个关子,我会在下一讲详细来讲。
那再回到优化排序上,由于只需要选取 Top K 个结果,因此我们可以使用堆排序来代替全排序。这样我们就能把排序的时间代价降低到 O(n) + O(k log n)(即建堆时间 + 在堆中选择最大的 k 个值的时间),而不是原来的 O(n log n)。举个例子,如果 k 是 1000,n 是 1000 万,那排序性能就提高了近 6 倍!这是一个非常有效的性能提升。
重点回顾
好了,今天的内容就先讲到这里。我们一起来回顾一下,你要掌握的重点内容。
首先,我们讲了 3 种打分方法,分别是经典算法 TF-IDF、概率模型 BM25 算法以及机器学习打分。
在 TF-IDF 中,TF 代表了词项在文档中的权重,而 IDF 则体现了词项的区分度。尽管 TF-IDF 很简单,但它是许多更复杂的打分算法的基础。比如说,在使用机器学习进行打分的时候,我们也可以直接将 TF-IDF 作为一个因子来处理。
BM25 算法则是概率模型中最成功的相关性打分算法。它认为 TF 对于相关性的影响是有上限的,所以,它不仅同时考虑了 IDF、文档长度、文档中的词频,以及查询词中的词频这四个因子,还给出了 3 个可以人工调整的参数。这让它的打分效果得到了广泛的认可,能够应用到很多检索系统中。
不过,因为机器学习可以更大规模地引入更多的打分因子,并且可以自动学习出各个打分因子的权重。所以,利用机器学习进行相关性打分,已经成了目前大规模检索引擎的标配。
完成打分阶段之后,排序阶段我们要重视排序的效率。对于精准 Top K 检索,我们可以使用堆排序来代替全排序,只返回我们认为最重要的 k 个结果。这样,时间代价就是 O(n) + O(k log n) ,在数据量级非常大的情况下,它比 O(n log n) 的检索性能会高得多。
课堂讨论
- 在今天介绍的精准 Top K 检索的过程中,你觉得哪个部分是最耗时的?是打分还是排序?
- 你觉得机器学习打分的优点在哪里?你是否使用过机器学习打分?可以把你的使用场景分享出来。
欢迎在留言区畅所欲言,说出你的想法。如果有收获,也欢迎把这一讲分享给你的朋友。
文章作者 anonymous
上次更新 2024-01-23