13|树的广度优先搜索(上):人际关系的六度理论是真的吗?
文章目录
你好,我是黄申。
上一节,我们探讨了如何在树的结构里进行深度优先搜索。说到这里,有一个问题,不知道你有没有思考过,树既然是两维的,我们为什么一定要朝着纵向去进行深度优先搜索呢?是不是也可以朝着横向来进行搜索呢?今天我们就来看另一种搜索机制,广度优先搜索。
社交网络中的好友问题
LinkedIn、Facebook、微信、QQ 这些社交网络平台都有大量的用户。在这些社交网络中,非常重要的一部分就是人与人之间的“好友”关系。
在数学里,为了表示这种好友关系,我们通常使用图中的结点来表示一个人,而用图中的边来表示人和人之间的相识关系,那么社交网络就可以用图论来表示。而“相识关系”又可以分为单向和双向。
单向表示,两个人 a 和 b,a 认识 b,但是 b 不认识 a。如果是单向关系,我们就需要使用有向边来区分是 a 认识 b,还是 b 认识 a。如果是双向关系,双方相互认识,因此直接用无向边就够了。在今天的内容里,我们假设相识关系都是双向的,所以我们今天讨论的都是无向图。

从上面的例图可以看出,人与人之间的相识关系,可以有多条路径。比如,张三可以直接连接赵六,也可以通过王五来连接赵六。比较这两条通路,最短的通路长度是 1,因此张三和赵六是一度好友。也就是说,这里我用两人之间最短通路的长度,来定义他们是几度好友。照此定义,在之前的社交关系示意图中,张三、王五和赵六互为一度好友,而李四和赵六、王五为二度好友。

寻找两个人之间的最短通路,或者说找出两人是几度好友,在社交中有不少应用。例如,向你推荐新的好友、找出两人之间的关系的紧密程度、职场背景调查等等。在 LinkedIn 上,有个功能就是向你推荐了你可能感兴趣的人。下面这张图是我的 LinkedIn 主页里所显示的好友推荐。

这些被推荐的候选人,和我都有不少的共同连接,也就是共同好友。所以他们都是我的二度好友。但是,他们和我之间还没有建立直接的联系,因此不是一度好友。也就是说,对于某个当前用户,LinkedIn 是这么来选择好友推荐的:
- 被推荐的人和当前用户不是一度好友;
- 被推荐的人和当前用户是二度好友。
那为什么我们不考虑“三度“甚至是“四度”好友呢?我前面已经说过,两人之间最短的通路长度,表示他们是几度好友。那么三度或者四度,就意味着两人间最短的通路也要经历 2 个或更多的中间人,他们的关系就比较疏远,互相添加好友的可能性就大大降低。
所以呢,总结一下,如果我们想进行好友推荐,那么就要优先考虑用户的“二度“好友,然后才是“三度”或者“四度”好友。那么,下一个紧接着要面临的问题就是:给定一个用户,如何优先找到他的二度好友呢?
深度优先搜索面临的问题
这种情况下,你可能会想到上一篇介绍的深度优先搜索。深度优先搜索不仅可以用在树里,还可以应用在图里。不过,我们要面临的问题是图中可能存在回路,这会增加通路的长度,这是我们在计算几度好友时所不希望的。所以在使用深度优选搜索的时候,一旦遇到产生回路的边,我们需要将它过滤。具体的操作是,判断新访问的点是不是已经在当前通路中出现过,如果出现过就不再访问。
如果过滤掉产生回路的边,从一个用户出发,我们确实可以使用深度优先的策略,搜索完他所有的 n 度好友,然后再根据关系的度数,从二度、三度再到四度进行排序。这是个解决方法,但是效率太低了。为什么呢?
你也许听说过社交关系的六度理论。这个理论神奇的地方在于,它说地球上任何两个人之间的社交关系不会超过六度。咋一听,感觉不太可能。仔细想想,假设每个人平均认识 100 个人(我真心不觉得 100 很多,不信你掰着指头数数看自己认识多少人),那么你的二度好友就是 100^2,这个可以用我们前面讲的排列思想计算而来。
以此类推,三度好友是 100^3,到五度好友就有 100 亿人了,已经超过了地球目前的总人口。即使存在一些好友重复的情况下,例如,你的一度好友可能也出现在你的三度好友中,那这也不可能改变结果的数量级。所以目前来看,地球上任何两个人之间的社会关系不会超过六度。
六度理论告诉我们,你的社会关系会随着关系的度数增加,而呈指数级的膨胀。这意味着,在深度搜索的时候,每增加一度关系,就会新增大量的好友。但是你仔细回想一下,当我们在用户推荐中查看可能的好友时,基本上不会看完所有推荐列表,最多也就看个几十个人,一般可能也就看看前几个人。所以,如果我们使用深度优先搜索,把所有可能的好友都找到再排序,那效率实在太低了。
什么是广度优先搜索?
更高效的做法是,我们只需要先找到所有二度的好友,如果二度好友不够了,再去找三度或者四度的好友。这种好友搜索的模式,其实就是我们今天要介绍的广度优先搜索。
广度优先搜索(Breadth First Search),也叫宽度优先搜索,是指从图中的某个结点出发,沿着和这个点相连的边向前走,去寻找和这个点距离为 1 的所有其他点。只有当和起始点距离为 1 的所有点都被搜索完毕,才开始搜索和起始点距离为 2 的点。当所有和起始点距离为 2 的点都被搜索完了,才开始搜索和起始点距离为 3 的点,如此类推。
我用上一节介绍深度优先搜索顺序的那棵树,带你看一下广度优先搜索和深度优先搜索,在结点访问的顺序上有什么不一样。
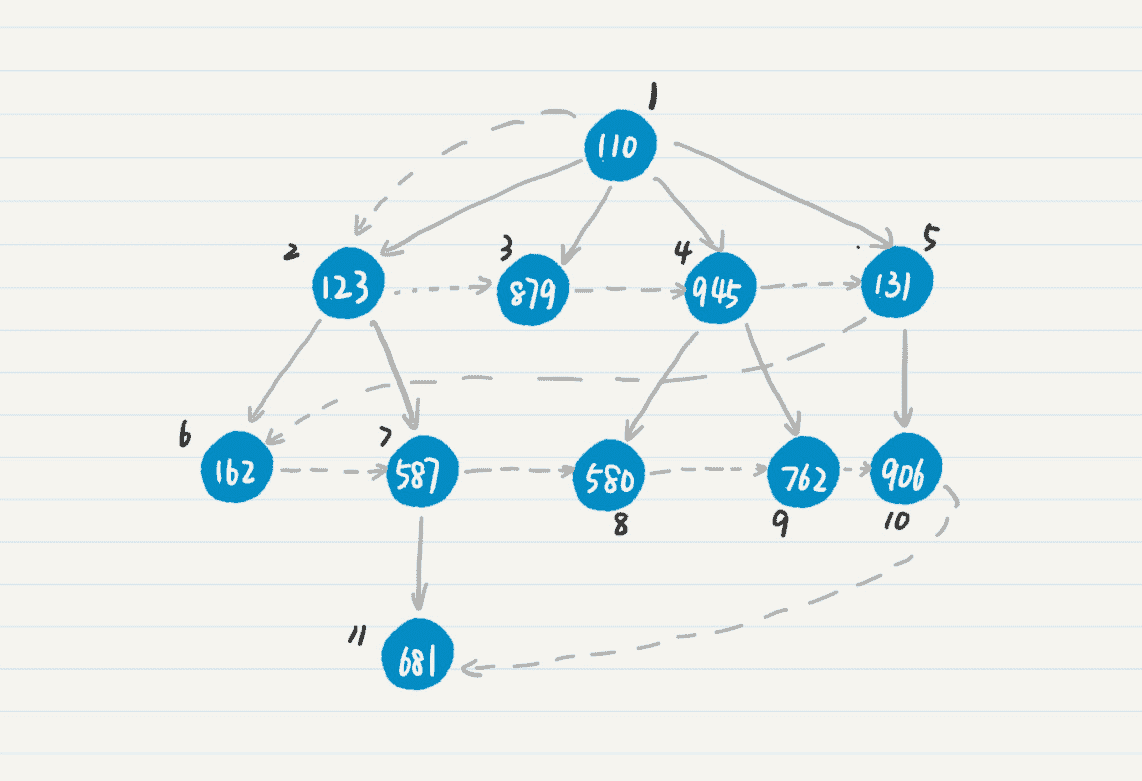
同样,我们用结点上的数字表示结点的 ID,用虚线表示遍历前进的方向,用结点边上的数字表示该结点在广度优先搜索中被访问的顺序。从这个图中,你有没有发现,广度优先搜索其实就是横向搜索一颗树啊!
尽管广度优先和深度优先搜索的顺序是不一样的,它们也有两个共同点。
第一,在前进的过程中,我们不希望走重复的结点和边,所以会对已经被访问过的点做记号,而在之后的前进过程中,就只访问那些还没有被标记的点。这一点上,广度优先和深度优先是一致的。有所不同的是,在广度优先中,如果发现和某个结点直接相连的点都已经被访问过,那么下一步就会看和这个点的兄弟结点直接相连的那些点,从中看看是不是有新的点可以访问。
例如,在上图中,访问完结点 945 的两个子结点 580 和 762 之后,广度优先策略发现 945 没有其他的子结点了,因此就去查看 945 的兄弟结点 131,看看它有哪些子结点可以访问,因此下一个被访问的点是 906。而在深度优先中,如果到了某个点,发现和这个点直接相连的所有点都已经被访问过了,那么不会查看它的兄弟结点,而是回退到这个点的父节点,继续查看和父结点直接相连的点中是不是存在新的点。例如在上图中,访问完结点 945 的两个子结点之后,深度优先策略会回退到点 110,然后访问 110 的子结点 131。
第二,广度优先搜索也可以让我们访问所有和起始点相通的点,因此也被称为广度优先遍历。如果一个图包含多个互不连通的子图,那么从起始点开始的广度优先搜索只能涵盖其中一个子图。这时,我们就需要换一个还没有被访问过的起始点,继续深度优先遍历另一个子图。深度优先搜索可以使用同样的方式来遍历有多个连通子图的图,这也回答了上一讲的思考题。
如何实现社交好友推荐?
第 12 讲中我说深度优先是利用递归的嵌套调用、或者是栈的数据结构来实现的。然而,广度优先的访问顺序是不一样的,我们需要优先考虑和某个给定结点距离为 1 的所有其他结点。等距离为 1 的结点访问完,才会考虑距离为 2 的结点。等距离为 2 的结点访问完,才会考虑距离为 3 的结点等等。在这种情况下,我们无法不断地根据结点的边走下去,而是要先遍历所有距离为 1 的点。
那么,如何在记录所有已被发现的结点情况下,优先访问距离更短的点呢?仔细观察,你会发现和起始点更近的结点,会先更早地被发现。也就是说,越早被访问到的结点,越早地处理它,这是不是很像我们平时排队的情形?早到的人可以优先接受服务,而晚到的人需要等前面的人都离开,才能轮到。所以这里我们需要用到队列这种先进先出(First In First Out)的数据结构。
如果你不是很熟悉队列的数据结构,我这里简短地回顾一下。队列是一种线性表,要被访问的下一个元素来自队列的头部,而所有新来的元素都会加入队列的尾部。
我画了张图给你讲队列的工作过程。首先,读取已有元素的时候,都是从队列的头部来取,例如 x1x1
文章作者 anonymous
上次更新 2024-03-12