你好，我是黄申，今天我们接着聊复杂度分析的实战。

上一讲，我从数学的角度出发，结合自身经验给你总结了几个分析复杂度的法则。但是在实际工作中我们会碰到很多复杂的问题，这个时候，正确地运用这些法则并不是件容易的事。今天，我就结合几个案例，教你一步步使用这几个法则。

案例分析一：广度优先搜索

在有关图遍历的专栏中，我介绍了单向广度优先和双向广度优先搜索。当时我提到了通常情况下，双向广度优先搜索性能更好。那么，我们应该如何从理论上分析，谁的效率更高呢？

首先我们来看单向广度优先搜索。我们先快速回顾一下搜索的主要步骤。

第一步，判断边界条件，时间和空间复杂度都是 O(1)。

第二步，生成空的队列。常量级的 CPU 和内存操作，根据主次分明法则，时间和空间复杂度都是 O(1)。

第三步，把搜索的起始结点放入队列 queue 和已访问结点的哈希集合 visited，类似上一步，常量级操作，时间和空间复杂度都是 O(1)。

第四步，也是最核心的步骤，包括了 while 和 for 的两个循环嵌套。

我们首先看时间复杂度。根据四则运算法则，时间复杂度是两个循环的次数相乘。对于嵌套在内的 for 循环，这个次数很好理解，和每个结点的直接连接点有关。如果要计算平均复杂度，我们就取直接连接点的平均数量，假设它为 m。

现在的难题在于，第一个 while 循环次数是多少呢？我们考虑一下齐头并进法则，是否存在其他的因素来决定计算的次数？第一次的 while 循环，只有起始点一个。从起始点出发，会找到 m 个一度连接点，把它们放入队列，那么第二次 while 循环就是 m 次，依次类推，到第 l 次，那么总次数就是 (m+m*m+m*m*m+…+m^l)。这里我们假设被重复访问的结点不多，可以忽略不计。

在循环内部，所有操作都是常量级的，包括通过哈希集合判断是否找到终止结点。所以时间复杂度就是 O(m+m*m+m*m*m+…+m^l)，取最高数量级 m^l，最后可以简化成 O(m^l)，其中 l 是从起始点开始所走的边数。这就是除了 m 之外的第二个关键因素。

如果你觉得还是不太好理解，可以使用一图千言法则，我画了一张图来帮助你理解。

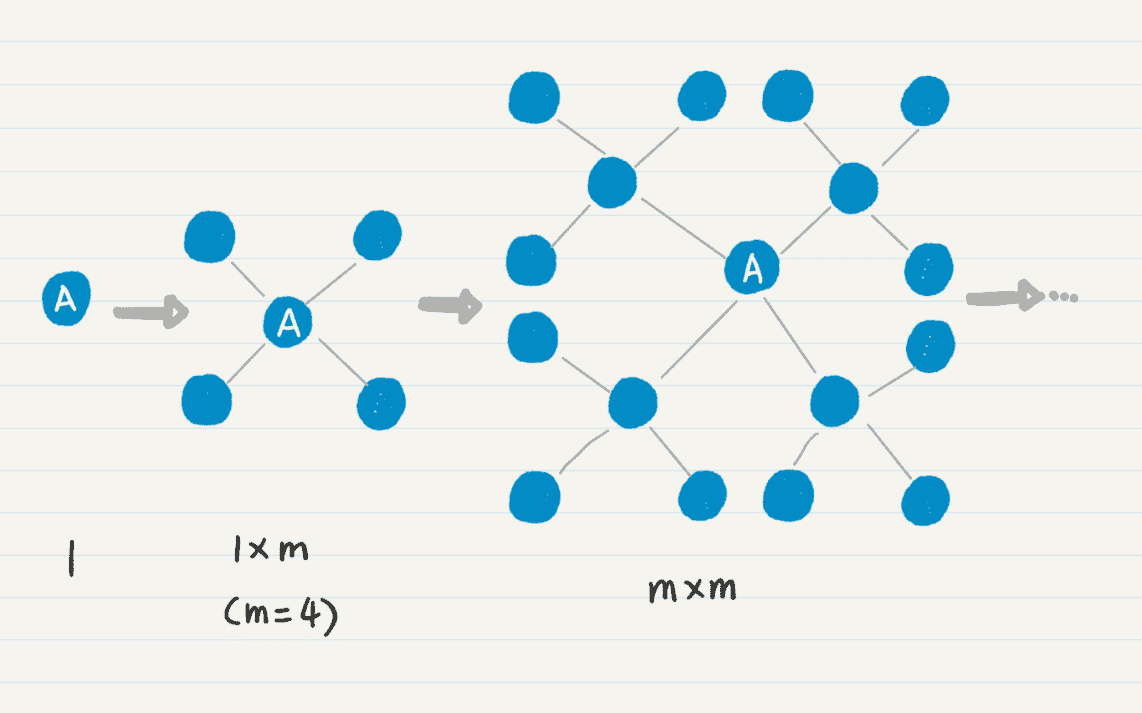
我们再来看这个步骤的空间复杂度。通过代码你应该可以看出来，只有 queue 和 visited 变量新增了数据，而图的结点本身没有发生改变。所以，考虑内存空间使用时，只需要考虑 queue 和 visited 的使用情况。两者都是在新发现一个结点时进行操作，因此新增的内存空间和被访问过的结点数成正比，同样为 O(m^l)。

最后，这四步是平行的，所以我们只需要把这几个时间复杂度相加就行了。很明显前三步都是常量，只有最后一步是决定性因素，因此时间和空间复杂度都是 O(m^l)。

我这里没有考虑图的生成，因为这步在单向搜索和双向搜索中是一样的，而且在实际项目中，我们也不会采用随机生成的方式。

接下来，我们来看看双向广度优先搜索。我刚才已经把单向的搜索过程分析得很透彻了，所以双向的复杂度你应该很容易就能得出来。但是，有两处关键点需要你注意。

第一个关键点是双向搜索所要走的边数。如果单向需要走 l 条边，那么双向是 l/2。因此时间和空间复杂度都会变为 O(2*m^(l/2)，简写为 O(m^(l/2))。这里 l/2 中的 2 不能省去，因为它是在指数上，改变了数量级。仅从这点来看，双向比单向的复杂度低。

第二个关键点是双向搜索过程中，判断是否找到通路的方式。单向搜索只需要判断一个点是否存在集合中，每次只有 O(1) 的复杂度。而双向搜索需要比较两个集合是否存在交集，复杂度肯定要高于 O(1)。最常规的实现方法是，循环遍历其中一个集合 A，看看 A 中的每个元素是不是出现在集合 B 中。假设两个集合中元素的数量都为 n，那么循环 n 次，那么时间复杂度就为 O(n)。基于这些，我们重新写一下双向广度优先搜索的时间复杂度。

假设我们分别从 aa