19|概率和统计:编程为什么需要概率和统计?
文章目录
你好,我是黄申。
通过第一个模块的学习,我想你对离散数学在编程领域中的应用,已经有了比较全面的认识。可以看出来,数据结构和基础算法体现的大多数都是离散数学的思想。这些思想更多的时候是给我们提供一种解决问题的思路,在具体指导我们解决问题的时候,我们还需要更多的数学知识。
比如说,在机器学习、数据挖掘等领域,概率统计就发挥着至关重要的作用。那关于概率统计,我们需要掌握哪些知识呢?这些知识究竟可以用在什么地方呢?第二模块的第一节,我们就来聊聊这些问题,让你对这一模块的学习做到心中有数。
概率和统计里有哪些需要掌握的概念?
在第一个模块中,我们认为所有事件都是一分为二的,要么必然发生,要么必然不发生。换句话说,事件的发生只有必然性,没有随机性。但是现实生活中,我们常常会碰到一些模棱两可的情况。
比如,你读到一则新闻,它报道了某个娱乐圈明星投资了一家互联网公司。那么,这则报道是属于娱乐新闻,还是科技新闻呢?你仔细读了读,觉得全篇大部分的内容都是讲述这家互联网企业的发展,而只有少部分的内容涉及了这位明星的私生活。你可能会说,这篇新闻 80% 的可能属于科技新闻,只有 20% 的可能属于娱乐新闻。这里面的数字表示了事件发生的可能性。概率(Probability)就是描述这种可能性的一个数值。
在概率的世界里,有很多概念。但是这几个非常基本的概念,你一定要知道。
我们用随机变量(Random Variable)来描述事件所有可能出现的状态,并使用概率分布(Probability Distribution)来描述每个状态出现的可能性。而随机变量又可以分为离散型随机变量(Discrete Random Variable)和连续型随机变量(Continuous Random Variable)。
这几个概念非常简单,但是其实也很抽象。我举个具体的例子,帮你加深印象。
假设我们使用一个随机变量 x 来表示新闻类型,如果在 100 篇新闻中,有 60 篇是娱乐新闻,有 20 篇是科技新闻,有 20 篇是体育新闻,那么你看到娱乐新闻的概率就是 60%,看到科技新闻的概率就是 20%,看到体育新闻的概率就是 20%。而这三组数据就可以构成变量 x 的概率分布P(x)。
在这个概率分布中,我们只有一个随机变量 x,现在我再添加另一个随机变量 y,表示新闻属于国际的还是国内的。这个时候,新的概率分布就需要由 x 和 y 这两个变量联合起来才能决定,我们把这种概率称为联合概率(Joint Probability)。
比如说,刚才那 100 篇新闻中有 30 篇是国际新闻,而这 30 篇中有 5 篇是科技新闻,那么国际科技新闻的联合概率就是 5/100=5%。不同的 x 和 y 取值的组合,就对应了不同的联合概率,我们用 P(x, y) 来表示。
对于离散型随机变量,通过联合概率 P(x, y) 在 y 上求和,就可以得到 P(x),这个 P(x) 就是边缘概率(Marginal Probability)。对于连续型随机变量,我们可以通过联合概率 P(x, y) 在 y 上的积分,推导出边缘概率 P(x)。边缘概率有啥用呢?有的时候,情况看起来很复杂,而我们其实只需要研究单个事件对概率分布的影响就可以了。这个时候,边缘概率可以帮助我们去除那些我们不需要关心的事件,把联合概率转换为非联合概率,例如从 P(x, y) 得到 P(x),从而忽略 y 事件。
对于多个随机变量,还有一个很重要的概念是条件概率。我估计很多人可能搞不清楚这个概念。我还是举例子跟你说。比如说,我们现在假设 100 篇中有 30 篇是国际新闻,而这 30 篇中有 5 篇是科技新闻,那在国际新闻中出现科技新闻的概率是多少呢?
这时候,我们就需要条件概率了。也就是某个事件受其他事件影响之后出现的概率,放到咱们的例子里,在国际新闻中出现科技新闻的概率就是 5/30=16.67%,在科技新闻中出现国际新闻的概率就是 5/20=25%。
说了这么多,不知道你有没有一种感觉,其实概率论研究的就是这些概率之间相互转化的关系,比如联合概率、条件概率和边缘概率。通过这些关系,概率论中产生了著名的贝叶斯定理(Bayes’theorem)。加上变量的独立性,我们就可以构建朴素贝叶斯(Naive Bayes)分类算法,这个算法在机器学习中的应用非常广泛,我们后面也会有一节课专门来讲。
此外,基于概率发展而来的信息论,提出了很多重要的概率,例如信息熵(Entropy)/ 香农熵(Shannon Entropy)、信息增益(Information Gain)、基尼指数(Gini)等。这些概念都被运用到了决策树(Decision Tree)的算法中。
提到概率论,就一定要提统计学。这是因为,概率和统计 **其实是互逆的。**怎么个互逆呢?概率论是对数据产生的过程进行建模,然后研究某种模型所产生的数据有什么特性。而统计学正好相反,它需要通过已知的数据,来推导产生这些数据的模型是怎样的。因此统计特别关注数据的各种分布、统计值及其对应的统计意义。
比如,现在有一大堆的新闻稿,我们想知道这里面有多少是娱乐新闻,有多少是科技新闻等等。我们可以先拿出一小部分采样数据,逐个来判断它属于哪个类型。比如说,分析了 10 篇之后,我们发现有 7 篇是科技新闻,2 篇是娱乐新闻,1 篇是体育新闻,那么从统计结果来看,三个类型的概率分别是 70%、20% 和 10%。然后,我们根据从这个小采样得来的结论,推测出科技新闻、娱乐新闻和体育新闻所占的比例。这就是统计学要做的事情。
在真实的世界里,我们通常只能观测到一些数据,而无法事先知道,是什么模型产生了这些数据,这时候就要依赖统计学。所以,海量数据的分析、实验和机器学习,都离不开统计学。
概率和统计可以帮我们做什么?
弄清楚这些基本概念之后,我们来看看概率和统计的知识能帮我们做点什么。
首先,我还是要提到复杂度分析。你可能会奇怪,之前讨论的复杂度分析好像没有涉及到概率啊。这是因为,在计算平均复杂度的时候,我们其实做了一个假设:所有情况出现的概率都是一样的。
我以最简单的查找算法为例。假设一个数组包含了 n 个元素,我们对其中的元素采取逐个扫描的方式,来查找其中的某个元素。如果这个元素一定会被找到,那么最好时间复杂度是 O(1),最差时间复杂度是 O(n),平均时间复杂度是 O((n+1)/2)。
等等,为什么平均复杂度是 O((n+1)/2) 呢?我们假设一共扫描了 n 次,第 1 次扫描了 1 个元素,第 2 次扫描了 2 个元素,一直到第 n 次扫描了 n 个元素,那么总共的扫描次数是 (1+2+…+n) = ((n+1)*n)/2,然后除以 n 次,得到每次扫描的元素数量平均值是 (n+1)/2,所以时间复杂度就是 O((n+1)/2)。
我把上述求和式改写成下面这样:
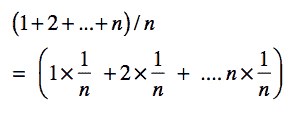
如果 1/n 是每种情况发生的概率,那么平均的扫描次数就是,不同情况下扫描次数按照概率进行的加权平均。问题来了,为什么这 n 种情况发生的概率都是 1/n 呢?这是因为之前我们做了一个默认的假设,我们每种情况发生的概率是一样的。但在实际生活中,概率很可能不是均匀分布的。
比如说,一个网站要对它的用户发放优惠券,那我们就需要先找到这些用户。我们用一个长度为 n 的数组代表某个网站的用户列表。我们假设第一个注册用户 ID 是 1,第二个注册用户的 ID 是 2,以此类推,最近刚刚注册的用户 ID 为 n。如果网站的发放策略是倾向于奖励新用户,那么被查找的用户 ID 有很大的概率会非常接近 n,因此平均复杂度就会非常接近 O(n)。相反,如果网站的发放策略是倾向于奖励老用户,那么搜索的用户 ID 有很大的概率是非常接近 1 的,因此平均复杂度会非常接近 O(1)。
你可以看到,现实中每种情况出现的可能性是不一样的,这也就意味者概率分布其是不均匀的。而不均匀的概率分布,最终会影响平均复杂度的加权平均计算。因此,要想获得更加准确的复杂度分析结果,我们必须要学习概率知识。
除此之外,概率和统计对于机器学习和大数据分析而言更为重要。对于机器学习而言,统计的运用是显而易见的。机器学习中的监督式学习,就是通过训练样本,估计出模型的参数,最后使用训练得出的模型,对新的数据进行预测。通过训练样本来估计模型,我们可以交给统计来完成。在机器学习的特征工程步骤中,我们可以使用统计的正态分布,标准化(standardization)不同取值范围的特征,让它们具有可比性。
此外,对机器学习算法进行效果评估时,AB 测试可以减少不同因素对评测结果的干扰。为了获得更可靠的结论,我们需要理解统计意义,并为每个 AB 测试计算相应的统计值。
最后,概率模型从理论上对某些机器学习算法提供了支持。朴素贝叶斯分类充分利用了贝叶斯定理,使用先验概率推导出后验概率,并通过变量之间相互独立的假设,把复杂的计算进行大幅的简化。简化之后,我们就可以把这个算法运用在海量文本的分类任务上。
而决策树使用了信息熵和信息增益,挑出最具有区分力的条件,构建决策树的结点和分支。这样构建出的树,不仅分类效率更高,而且更利于人脑的理解。谷歌的 PageRank 算法利用马尔科夫链的概率转移,有效地刻画了人们浏览互联网的行为,大幅提升了互联网搜索的体验。
学习这部分内容,需要做哪些准备?
听我说了这么多专栏的内容,你是不是有点担心,专栏的内容太深奥,不好理解。甚至在想,有没有必要做些准备?
学习不是件容易的事,因此进步的过程,从来不会轻松。努力需要你自己来,但是我也会从我的角度出发助力你的学习。我会争取讲清楚每个知识点背后的前因后果,以及不同知识点之间的联系,避免平铺直叙地罗列一堆理论和公式。但是,这部分内容,有公式是不可避免的,我尽量只保留那些最核心的公式。因此,即使你之前不太了解概率和统计,也没有关系。只有跟着我的节奏,搞懂每一节的重点,相信你很快就能领悟其中的精髓。
另外,我们无法脱离应用来讲知识,不然就本末倒置了。毕竟,我们学任何知识,都是为了用的。机器学习的知识纷繁复杂,涉及广泛,很多问题甚至是跨学科、跨领域的。不过,你不用担心,这里面会有太多看不懂的名词。我在讲解的时候,尽量给你抽象出最核心的部分,讲清楚来龙去脉,让你了解它整体的运作方式,不影响你对核心知识点的吸收。
当然,你可以适度地补一些概率知识,这样理解起来会更快。我在之前的加餐三中推荐了几本书,你可以找来看看,了解一些基本概念。另外,你可以准备一些实际工作和项目中的问题。例如,你之前参与的任务,哪些可以使用概率论来解决?碰到的难题有哪些?你是如何解决的?带着这些问题,再来看我的专栏,并且多在留言区写下你的疑问和收获,相信会有到事半功倍的效果。
小结
概率中的概念看起来很多,但是,其实最重要就是你耳熟能详的这几个:随机变量、概率分布、联合概率、条件概率和边缘概率。它们是整个概率的基础,我后面会详细来讲。
通过这些概念之间的相互推导,我们可以得到贝叶斯定理,这是朴素贝叶斯等系列算法的核心。而在概率基础之上发展而来的信息论,定义了信息熵、信息增益和基尼指数等,构成了决策树等系列算法的核心。
概率研究的是模型如何产生数据,统计研究的是如何通过数据来推导其背后的模型。所以说,概率和统计其实是互逆的。
概率和统计的运用非常多,我这里主要讲了三个方面。第一,概率可以帮助我们进行更精准的复杂度分析;第二,概率统计更多的是用在机器学习和大数据分析中;第三,概率统计还可以用在各种机器学习的算法中。这些内容,在之后的章节我会进行非常详细的讲解。
思考题
之前你对概率统计的认识是什么样的呢?对这块内容,你觉得最难的是什么?
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。

文章作者 anonymous
上次更新 2024-03-12