你好，我是黄申。

上一节，我们介绍了基于概率的语言模型。概率语言模型的研究对象其实是一个词的序列，以及这个词序列出现的概率有多大。那语言模型是不是也可以用于估算其他序列出现的概率呢？答案是肯定的。

通过上一节我们知道，语言模型中有个重点：马尔科夫假设及对应的多元文法模型。如果我们把这一点进一步泛化，就能引出马尔科夫模型。也就是说，只要序列的每个状态之间存在转移的概率，那么我们就可以使用马尔科夫模型。有时候情况会更复杂，不仅每个状态之间的转移是按照一定概率进行的，就连每个状态本身也是按照一定概率分布出现的，那么还需要用到隐马尔科夫模型。

今天这一节，我们就来学习马尔科夫模型、隐马尔科夫模型，以及它们在 PageRank 和中文分词中的应用。

马尔科夫模型

在介绍语言模型的时候，我们提到了马尔科夫假设，这个假设是说，每个词出现的概率和之前的一个或若干个词有关。我们换个角度思考就是，每个词按照一定的概率转移到下一个词。怎么个转移呢？我来解释一下。

如果把词抽象为一个状态，那么我们就可以认为，状态到状态之间是有关联的。前一个状态有一定的概率可以转移到到下一个状态。如果多个状态之间的随机转移满足马尔科夫假设，那么这类随机过程就是一个马尔科夫随机过程。而刻画这类随机过程的统计模型，就是马尔科夫模型（Markov Model）。

前面讲多元文法的时候，我提到了二元文法、三元文法。对于二元文法来说，某个词出现的概率只和前一个词有关。对应的，在马尔科夫模型中，如果一个状态出现的概率只和前一个状态有关，那么我们称它为一阶马尔科夫模型或者马尔科夫链。对应于三元、四元甚至更多元的文法，我们也有二阶、三阶等马尔科夫模型。

我们先从最简单的马尔科夫模型 - 马尔科夫链开始看。我画了一张示意图，方便你理解马尔科夫链中各个状态的转移过程。

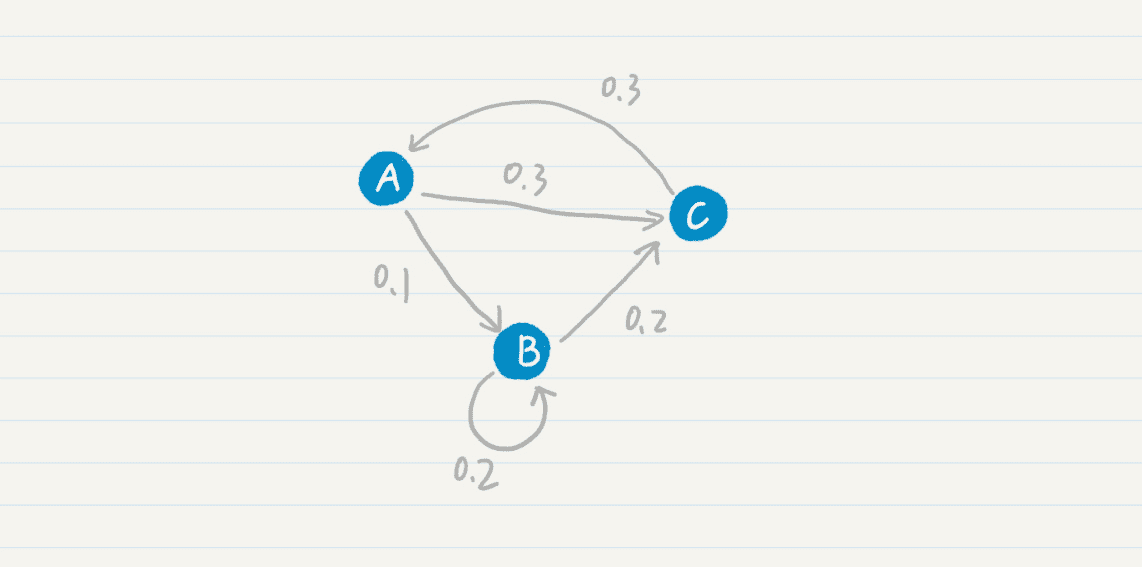
在这张图中，你可以看到，从状态 A 到 B 的概率是 0.1，从状态 B 到状态 C 的概率是 0.2 等等。我们也可以使用状态转移表来表示这张图。

我们可以根据某个应用的需要，把上述状态转移表具体化。例如，对于语言模型中的二元文法模型，我这里列出了一个示意表。

当然，除了二元文法模型，马尔科夫链还有很多应用的场景。

Google 公司最引以为傲的 PageRank 链接分析算法，它的核心思想就是基于马尔科夫链。这个算法假设了一个“随机冲浪者”模型，冲浪者从某张网页出发，根据 Web 图中的链接关系随机访问。在每个步骤中，冲浪者都会从当前网页的链出网页中随机选取一张作为下一步访问的目标。在整个 Web 图中，绝大部分网页节点都会有链入和链出。那么冲浪者就可以永不停歇地冲浪，持续在图中走下去。

在随机访问的过程中，越是被频繁访问的链接，越是重要。可以看出，每个节点的 PageRank 值取决于 Web 图的链接结构。假如一个页面节点有很多的链入链接，或者是链入的网页有较高的被访问率，那么它也将会有更高的被访问概率。

那么，PageRank 的公式和马尔科夫链有什么关系呢？我先给你看一张 Web 的拓扑图。

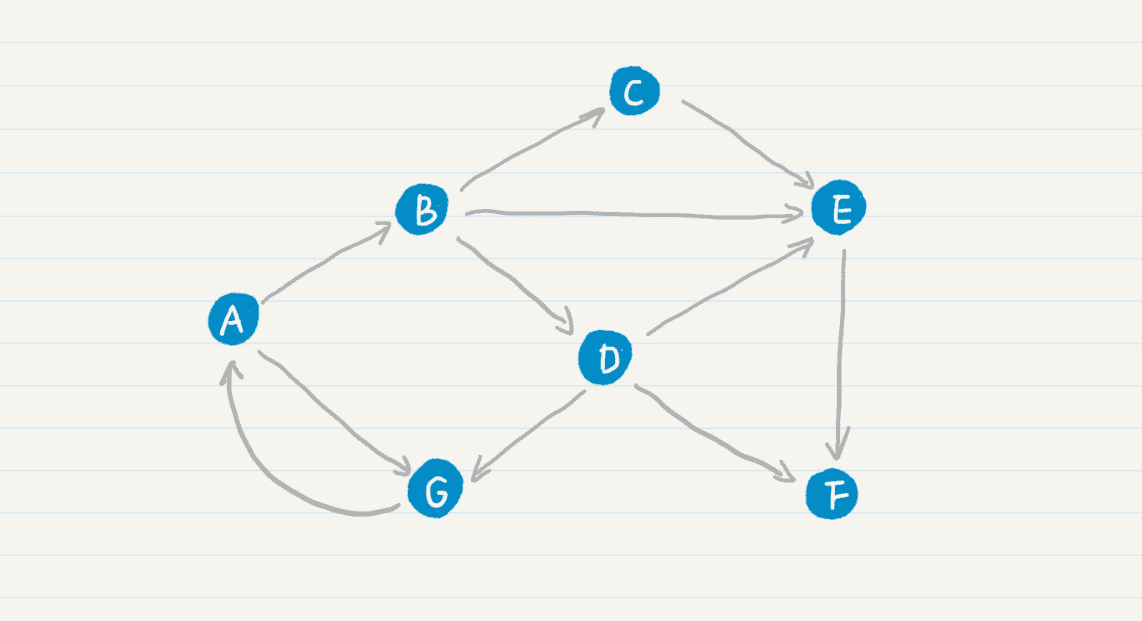
其中 A、B、C 等结点分别代表了页面，而结点之间的有向边代表了页面之间的超链接。看了这张图中，你是不是觉得 Web 拓扑图和马尔科夫链的模型图基本上是一致的？我们可以假设每张网页就是一个状态，而网页之间的链接表明了状态转移的方向。这样，我们很自然地就可以使用马尔科夫链来刻画“随机冲浪者”。

另外，在最基本的 PageRank 算法中，我们可以假设每张网页的出度是 nn