你好，我是黄申。

之前和你聊了概率在朴素贝叶斯分类算法中的应用。其实，概率在很多像信息论这样的应用数学领域都有广泛的应用。信息论最初就是运用概率和统计的方法，来研究信息传递的。最近几十年，人们逐步开始使用信息论的概念和思想，来描述机器学习领域中的概率分布，并衡量概率分布之间的相似性。随之而来的是，人们发明了不少相关的机器学习算法。所以接下来的几节，我来介绍一些基于信息论知识的内容。

信息论的概念比较枯燥，为了让你更轻松地学习，让我从一个生动的案例开始。最近我在朋友圈看到一个小游戏，叫“测一测你是金庸笔下的哪个人物？”。玩这个游戏的步骤是，先做几道题，然后根据你的答案，生成对应的结果。下面是我几位朋友答题之后得到的结果。

这种测试挺好玩的，而且好像有很多类似的，比如测星座啊、测运势啊等等。那你知道这种心理或者性格测试的题目是怎么设计的吗？

通常，这种心理测试会有一个题库，包含了许多小题目，也就是从不同的方面，来测试人的性格。不过，针对特定的测试目标，我们可能没必要让被测者回答所有的问题。那么，问卷设计者应该如何选择合适的题目，才能在读者回答尽量少的问题的同时，相对准确地测出自己是什么“性格”呢？这里，我们就需要引入基于概率分布的信息熵的概念，来解决这个问题。

什么是信息熵？

我还是拿刚刚那个“测测你是哪个武侠人物”的小游戏举例子。我设计了一个测试题，你可以看看下面这个图表。这个表里一共有 10 个人物。每个人物都有性别、智商、情商、侠义和个性共 5 个属性。相应地，我会设计 5 道题目分别测试这 5 个属性所占的比例。最后，将测出的 5 个属性和答案中的武侠人物对照，就可以找到最接近的答案，也就是被测者对应的武侠人物。

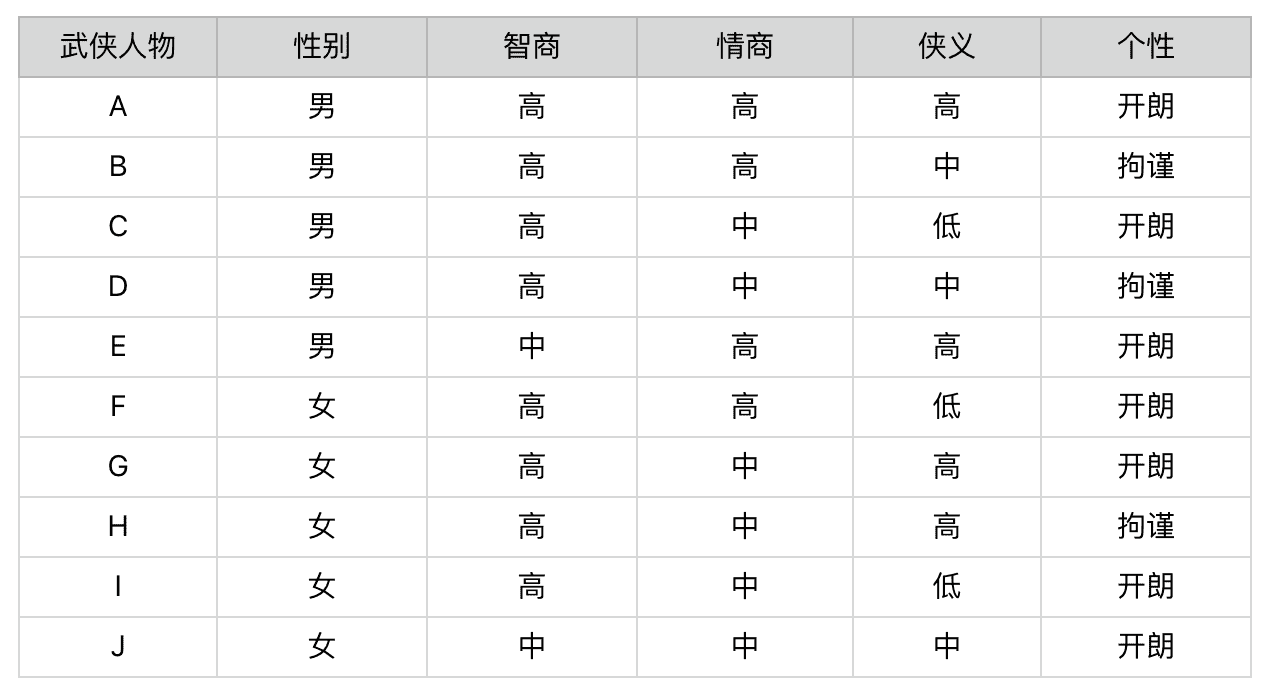
这个过程非常简单，你应该很容易就能理解。在这个设计过程中，起决定性作用的环节其实就是，如何设计这 5 道题目。比如，题目的先后顺序会不会直接影响要回答问题的数量？每个问题在人物划分上，是否有着不同的区分能力？这些都是信息熵要解决的问题。

我们先来看，这里的区分能力指的是什么呢？每一个问题都会将被测试者划分为不同的人物分组。如果某个问题将属于不同人物分组的被测者，尽可能地划分到了相应的分组，那么我们认为这个问题的区分能力较强。相反，如果某个问题无法将属于不同人物分组的被测者划分开来，那么我们认为这个问题的区分能力较弱。为了帮你进一步理解，我们先来比较一下“性别”和“智商”这两个属性。

首先，性别属性将武侠人物平均地划分为一半一半，也就是说“男”和“女”出现的先验概率是各 50%。如果我们假设被测试的人群，其男女性别的概率分布也是 50% 和 50%，那么关于性别的测试题，就能将被测者的群体大致等分。

我们再来看智商属性。我们也将武侠人物划分为 2 个小集合，不过“智商高”的先验概率是 80%，而“智商中等”的先验概率只有 20%。同样，我们假设被测试的人群，其智商的概率分布也是类似地，那么经过关于智商的测试题之后，仍然有 80% 左右的不同人物还是属于同一个集合，并没有被区分开来。因此，我们可以认为关于“智商”的测试题，在对人物进行分组这个问题上，其能力要弱于“性别”的测试题。

上述这些是不是都很简单？这些都是我们按照感觉，或者说经验来划分的。现在，我们试着用两个科学的度量指标，信息熵（Entropy）和信息增益（Information Gain），来衡量每道题目的区分能力。

首先，怎么来理解信息熵呢？信息熵，我们通常简称为熵，其实就是用来刻画给定集合的纯净度的一个指标。你可能要问了，那纯净度是啥呢？我举个例子给你解释一下。比如说，一个集合里的元素全部是属于同一个分组，这个时候就表示最纯净，我们就说熵为 0；如果这个集合里的元素是来自不同的分组，那么熵是大于 0 的值。其具体的计算公式如下：

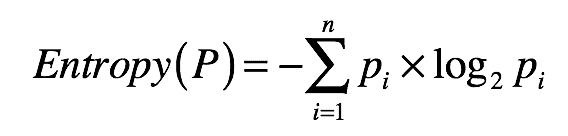
其中，nn