30|统计意义(上):如何通过显著性检验,判断你的A/B测试结果是不是巧合?
文章目录
你好,我是黄申,今天我们来聊聊统计意义和显著性检验。
之前我们已经讨论了几种不同的机器学习算法,包括朴素贝叶斯分类、概率语言模型、决策树等等。不同的方法和算法会产生不同的效果。在很多实际应用中,我们希望能够量化这种效果,并依据相关的数据进行决策。
为了使这种量化尽可能准确、客观,现在的互联网公司通常是根据用户的在线行为来评估算法,并比较同类算法的表现,以此来选择相应的算法。在线测试有一个很大的挑战,那就是如何排除非测试因素的干扰。

从图中可以看出,自 2016 年 1 月 12 日开始,转化率曲线的趋势发生了明显的变化。假如说这天恰好上线了一个新版的技术方案 A,那么转化率上涨一定是新方案导致的吗?不一定吧?很有可能,1 月 12 日有个大型的促销,使得价格有大幅下降,或者有个和大型企业的合作引入了很多优质顾客等,原因有非常多。如果我们取消 12 日上线的技术方案 A,然后用虚线表示在这种情况下的转化率曲线,这个时候得到了另一张图。
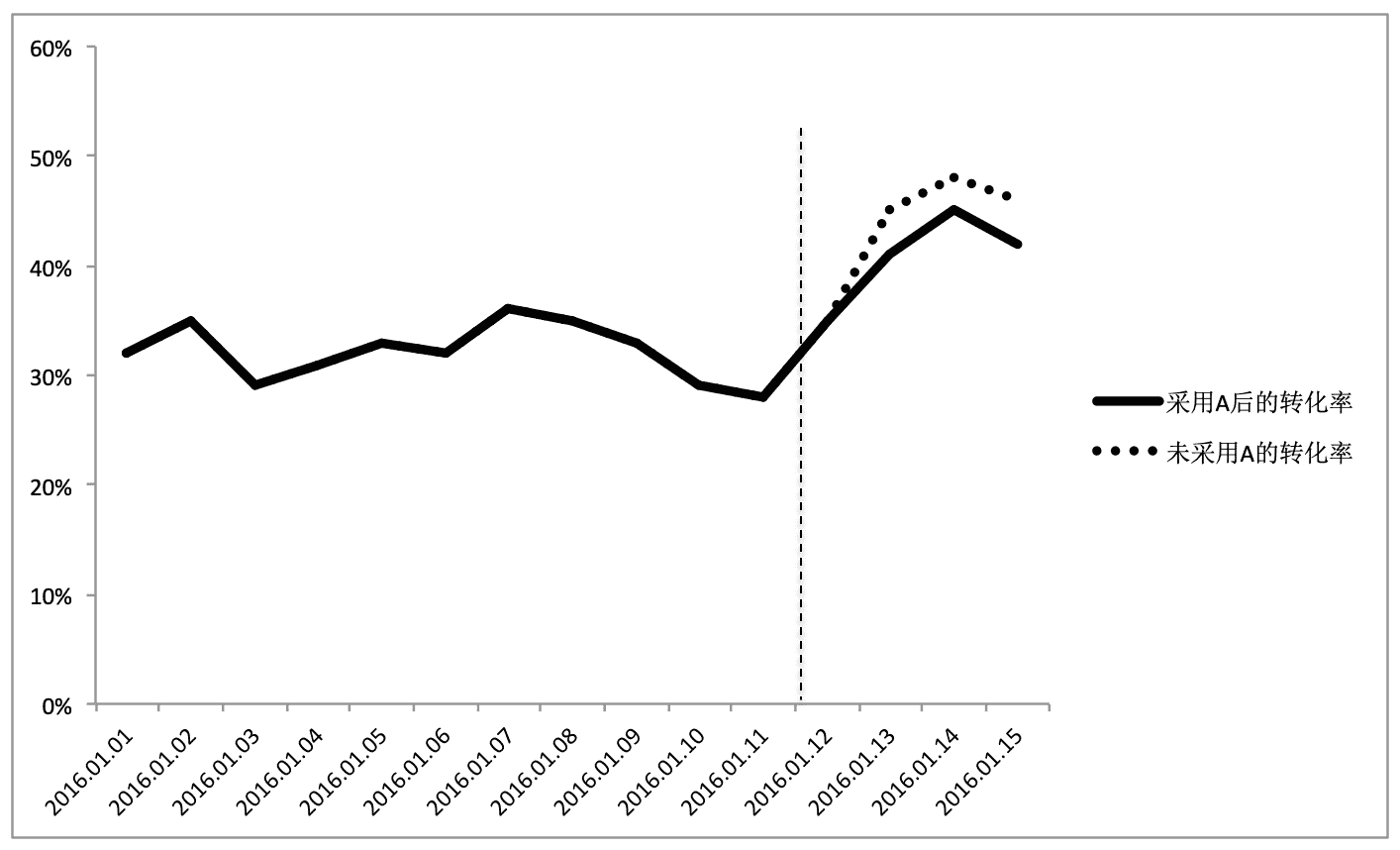
从图中可以发现,不用方案 A,反而获得了更好的转化率表现,所以,简单地使用在线测试的结果往往会导致错误的结论,我们需要一个更健壮的测试方法,A/B 测试。
A/B 测试,简单来说,就是为同一个目标制定两个或多个方案,让一部分用户使用 A 方案,另一部分用户使用 B 方案,记录下每个部分用户的使用情况,看哪个方案产生的结果更好。这也意味着,通过 A/B 测试的方式,我们可以拿到使用多个不同方法之后所产生的多组结果,用于对比。
问题来了,假设我们手头上有几组不同的结果,每组对应一个方案,包含了最近 30 天以来每天的转化率,如何判断哪个方案的效果更好呢?你可能会想,对每一组的 30 个数值取平均数,看看谁的均值大不就好了?但是,这真的就够了吗?
假设有两组结果需要比较,每一组都有 5 个数据,而且这两组都符合正态分布。我用一张图画一下这两个正态分布之间的关系。
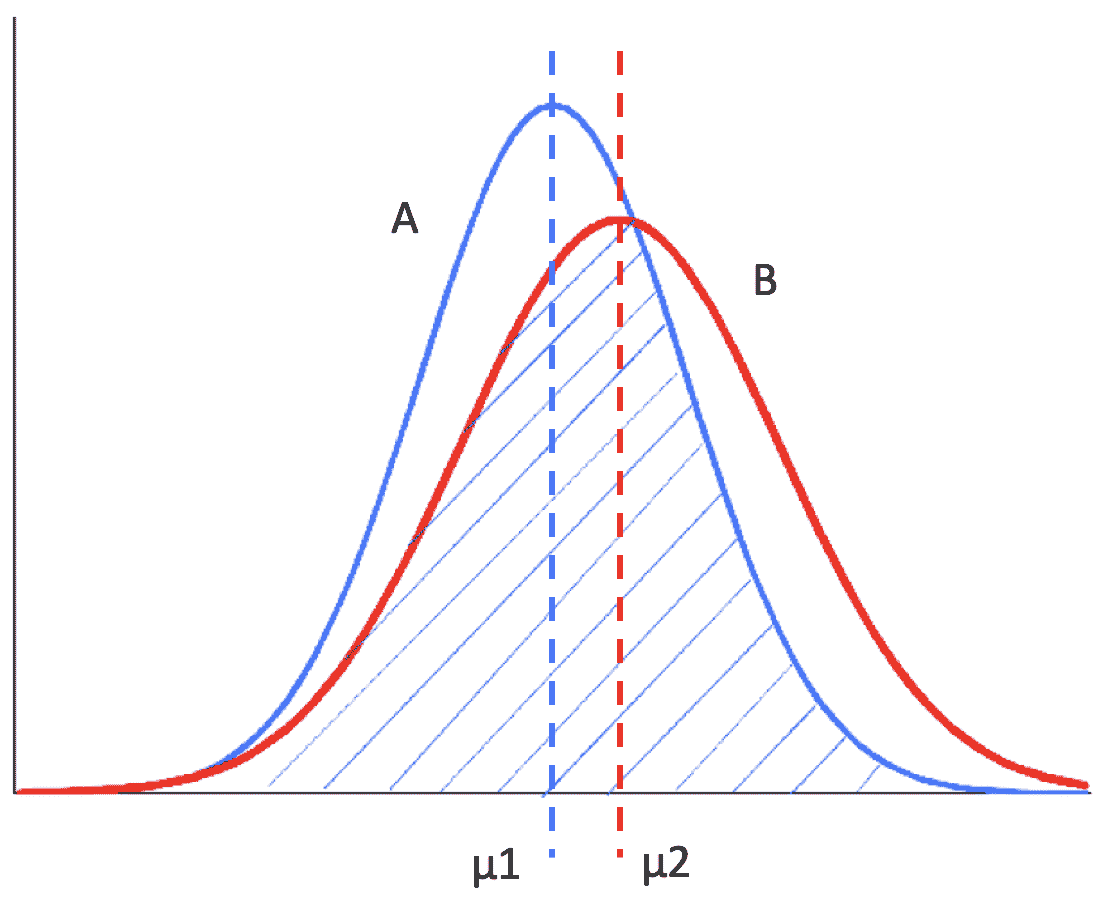
从这张图可以看出,左边的正态分布 A 均值μ1 比较小,右侧的正态分布 B 均值μ2 比较大。可是,如果我们无法观测到 A 和 B 这两个分布的全部,而只根据这两个分布的采样数据来做判断,会发生什么情况?我们很有可能会得出错误的结论。

比如说,在这张图的采样中,红色的点表示 B 的采样,它们都是来自 B 分布的左侧,而蓝色的点表示 A 的采样,它们都是来自 A 分布的右侧。如果我们仅仅根据这两组采样数据的均值来判断,很可能会得出“B 分布的均值小于 A 分布均值”这样的错误结论。
A/B 测试面临的就是这样的问题。我们所得到的在线测试结果,实际上只是一种采样。所以我们不能简单地根据每个组的平均值,来判断哪个组更优。那有没有更科学的办法呢?在统计学中,有一套成熟的系统和对应的方法,今天我们就来讲讲这种方法。
为了让你能够充分理解这个,我先介绍几个基本概念,显著性差异、统计假设检验和显著性检验、以及 P 值。
显著性差异
从刚刚那两张正态分布图,我们可以分析得出,两组数据之间的差异可能由两个原因引起。
第一,两个分布之间的差异。假设 A 分布的均值小于 B 分布,而两者的方差一致,那么 A 分布随机产生的数据有更高的概率小于 B 分布随机产生的数据。第二,采样引起的差异,也就是说采样数据不能完全体现整体的数据分布。我在之前的图中,用来自 A、B 两组的 10 个数据展示了采样所导致的误差。
如果差异是第一个原因导致的,在统计学中我们就认为这两组“有显著性差异”。如果差异是第二种原因导致的,我们就认为这两组“无显著性差异”。可以看出来,显著性差异(Significant Difference),其实就是研究多组数据之间的差异,是由于不同的数据分布导致的,还是由于采样的误差导致的。通常,我们也把“具有显著性差异”,称为“差异具有统计意义”或者“差异具有显著性”。
这里你还需要注意“差异具有显著性”和“具有显著差异”的区别。如前所说,“差异具有显著性“表示不同的组很可能来自不同的数据分布,也就是说多个组的数据来自同一分布的可能性非常小。而“具有显著差异”,是指差异的幅度很大,比如相差 100 倍。
不过,差异的显著性和显著差异没有必然联系。举两个例子,比如说,两个不同的数据分布,它们的均值分别是 1 和 1.2,这两个均值相差的绝对值很小,也就是没有显著差异,但是由于它们源自不同的数据分布,所以差异是具有显著性的。再比如说,来自同一个数据分布的两个采样,它们的均值分别是 1 和 100,具有显著的差异,但是差异没有显著性。
统计假设检验和显著性检验
统计假设检验是指事先对随机变量的参数或总体分布做出一个假设,然后利用样本信息来判断这个假设是否合理。在统计学上,我们称这种假设为虚无假设(Null Hypothesis),也叫原假设或零假设,通常记作H0。而和虚无假设对立的假设,我们称为对立假设(Alternative Hypothesis),通常记作H1。也就是说,如果证明虚无假设不成立,那么就可以推出对立假设成立。
统计假设检验的具体步骤是,先认为原假设成立,计算其会导致什么结果。若在单次实验中产生了小概率的事件,则拒绝原假设 H0,并接受对立假设 H1。若不会产生小概率的事件,则不能拒绝原假设 H0,从而接受它。因此,统计学中的假设是否成立,并不像逻辑数学中的绝对“真”或“假”,而是需要从概率的角度出发来看。
那么,问题来了,多少才算是“小概率”呢?按照业界的约定俗成,通常我们把概率不超过 0.05 的事件称为“小概率事件”。当然,根据具体的应用,偶尔也会取 0.1 或 0.01 等。在假设检验中,我们把这个概率记为α,并称它为显著性水平。
显著性检验是统计假设检验的一种,顾名思义,它可以帮助我们判断多组数据之间的差异,是采样导致的“偶然”,还是由于不同的数据分布导致的“必然“。当然,这里的“偶然”和“必然”都是相对的,和显著性水平α有关。显著性检验的假设是,多个数据分布之间没有差异。如果样本发生的概率小于显著性水平α,证明小概率事件发生了,所以拒绝原假设,也就是说认为多个分布之间有差异。否则呢,接受原假设,认为多个分布之间没有差异。换句话说,显著性水平α即为拒绝原假设的标准。
P 值
既然已经定义了显著性检验和显著性水平,那么我们如何为多组数据计算它们之间差异的显著性呢?我们可以使用 P 值(P-value)。P 值中的 P 代表 Probability,就是当 H0 假设为真时,样本出现的概率,或者换句话说,其实就是我们所观测到的样本数据符合原假设 H0 的可能性有多大。
如果 P 值很小,说明观测值与假设 H0 的期望值有很大的偏离,H0 发生的概率很小,我们有理由拒绝原假设,并接受对立假设。P 值越小,表明结果越显著,我们越有信心拒绝原假设。反之,说明观测值与假设 H0 的期望值很接近,我们没有理由拒绝 H0。
在显著性检验中,原假设认为多个分组内的数据来自同一个数据分布,如果 P 值足够小,我们就可以拒绝原假设,认为多个分组内的数据来自不同的数据分布,它们之间存在显著性的差异。所以说,只要能计算出 P 值,我们就能把 P 值和显著性水平α进行比较,从而决定是否接受原假设。
总结
今天我从互联网公司常见的 A/B 测试实验入手,给你讲解了一个更科学的方法来比较不同算法的效果,它就是统计学里的差异显著性检验。这个方法包含了一些你平时可能不太接触的概念,你首先需要理解显著性差异、统计假设检验和 P 值。其中最为重要的就是显著性差异的概念,因为这是差异显著性检验区别于简单的平均值方法的关键。
为了便于你的记忆,我这里再用一个形象的比喻来带你复习一遍。
儿子考了 90 分,我问他:“你比班上平均分高多少?”如果他回答:“我不太确定,我只看到了周围几个人的分数,我猜大概高出了 10 分吧”,那么说明他对“自己分数比平均分高出 10 分”这个假设信心不足,结论有较大的概率是错误的,所以即使可能高了 10 分,我也高兴不起来。
如果他回答:“老师说了,班级平均分是 88 分,我比平均分高出了 2 分”,那我就很开心了,因为老师掌握了全局的信息,她说的话让儿子对“自己分数比平均分高出 2 分”的假设是非常有信心的。即使只高出了 2 分,但是结论有很大的概率是正确的。
理解了概念之后,我们就要进入实战环节了。其实显著性检验的具体方法有很多,例如方差分析(F 检验)、t 检验、卡方检验等等。不同的方法计算 P 值的方法也不同,在下一节,我会用 A/B 测试的案例来详细解释。
思考题
在对比两组数据的差异时,如果不断增加采样次数,也就是样本的数量,使用平均值和使用显著性检验这两者的结论,会不会逐渐变得一致?
欢迎留言和我分享,也欢迎你在留言区写下今天的学习笔记。你可以点击“请朋友读”,把今天的内容分享给你的好友,和他一起精进。

文章作者 anonymous
上次更新 2024-03-12