04|语法分析（二）：解决二元表达式中的难点

在“03 | 语法分析（一）：纯手工打造公式计算器”中，我们已经初步实现了一个公式计算器。而且你还在这个过程中，直观地获得了写语法分析程序的体验，在一定程度上破除了对语法分析算法的神秘感。

当然了，你也遇到了一些问题，比如怎么消除左递归，怎么确保正确的优先级和结合性。所以本节课的主要目的就是解决这几个问题，让你掌握像算术运算这样的二元表达式（Binary Expression）。

不过在课程开始之前，我想先带你简单地温习一下什么是左递归（Left Recursive）、优先级（Priority）和结合性（Associativity）。

在二元表达式的语法规则中，如果产生式的第一个元素是它自身，那么程序就会无限地递归下去，这种情况就叫做**左递归。**比如加法表达式的产生式“加法表达式 + 乘法表达式”，就是左递归的。而优先级和结合性则是计算机语言中与表达式有关的核心概念。它们都涉及了语法规则的设计问题。

我们要想深入探讨语法规则设计，需要像在词法分析环节一样，先了解如何用形式化的方法表达语法规则。“工欲善其事必先利其器”。熟练地阅读和书写语法规则，是我们在语法分析环节需要掌握的一项基本功。

所以本节课我会先带你了解如何写语法规则，然后在此基础上，带你解决上面提到的三个问题。

书写语法规则，并进行推导

我们已经知道，语法规则是由上下文无关文法表示的，而上下文无关文法是由一组替换规则（又叫产生式）组成的，比如算术表达式的文法规则可以表达成下面这种形式：

1
2
3
4
5
6



add -> mul | add + mul

mul -> pri | mul * pri

pri -> Id | Num | (add) 

按照上面的产生式，add 可以替换成 mul，或者 add + mul。这样的替换过程又叫做“推导”。以“2+3*5”和“2+3+4”这两个算术表达式为例，这两个算术表达式的推导过程分别如下图所示：

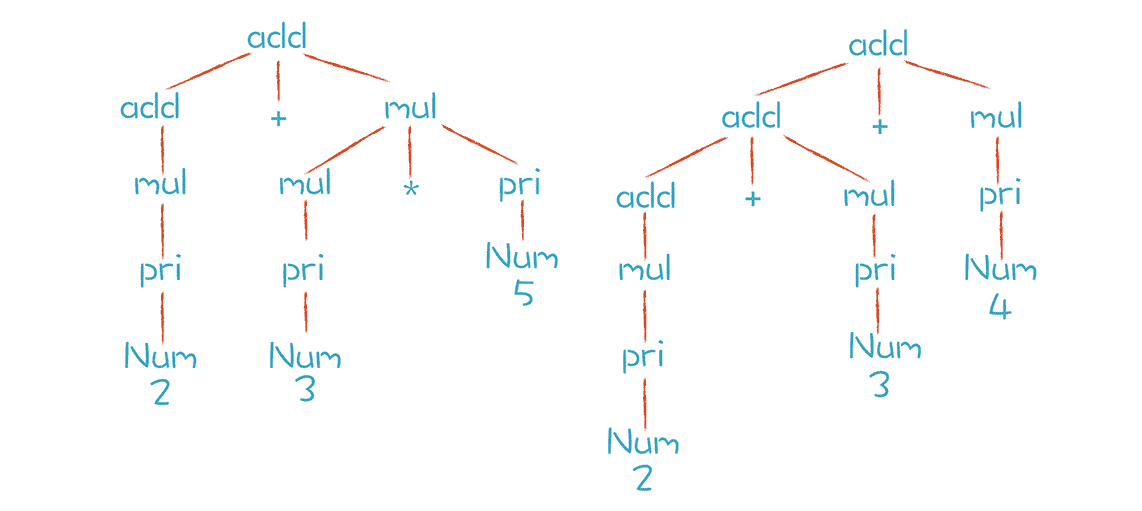
通过上图的推导过程，你可以清楚地看到这两个表达式是怎样生成的。而分析过程中形成的这棵树，其实就是 AST。只不过我们手写的算法在生成 AST 的时候，通常会做一些简化，省略掉中间一些不必要的节点。比如，“add-add-mul-pri-Num”这一条分支，实际手写时会被简化成“add-Num”。其实，简化 AST 也是优化编译过程的一种手段，如果不做简化，呈现的效果就是上图的样子。

那么，上图中两颗树的叶子节点有哪些呢？Num、+ 和 * 都是终结符，终结符都是词法分析中产生的 Token。而那些非叶子节点，就是非终结符。文法的推导过程，就是把非终结符不断替换的过程，让最后的结果没有非终结符，只有终结符。

而在实际应用中，语法规则经常写成下面这种形式：

1
2
3
4
5
6



add ::= mul | add + mul

mul ::= pri | mul * pri

pri ::= Id | Num | (add) 

这种写法叫做**“巴科斯范式”，**简称 BNF。Antlr 和 Yacc 这两个工具都用这种写法。为了简化书写，我有时会在课程中把“::=”简化成一个冒号。你看到的时候，知道是什么意思就可以了。

你有时还会听到一个术语，叫做**扩展巴科斯范式 (EBNF)。**它跟普通的 BNF 表达式最大的区别，就是里面会用到类似正则表达式的一些写法。比如下面这个规则中运用了 * 号，来表示这个部分可以重复 0 到多次：

1
2

add -> mul (+ mul)*

其实这种写法跟标准的 BNF 写法是等价的，但是更简洁。为什么是等价的呢？因为一个项多次重复，就等价于通过递归来推导。从这里我们还可以得到一个推论：就是上下文无关文法包含了正则文法，比正则文法能做更多的事情。

确保正确的优先级

掌握了语法规则的写法之后，我们来看看如何用语法规则来保证表达式的优先级。刚刚，我们由加法规则推导到乘法规则，这种方式保证了 AST 中的乘法节点一定会在加法节点的下层，也就保证了乘法计算优先于加法计算。

听到这儿，你一定会想到，我们应该把关系运算（>、=、<）放在加法的上层，逻辑运算（and、or）放在关系运算的上层。的确如此，我们试着将它写出来：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14



exp -> or | or = exp   

or -> and | or || and

and -> equal | and && equal

equal -> rel | equal == rel | equal != rel

rel -> add | rel > add | rel < add | rel >= add | rel <= add

add -> mul | add + mul | add - mul 

mul -> pri | mul * pri | mul / pri 

这里表达的优先级从低到高是：赋值运算、逻辑运算（or）、逻辑运算（and）、相等比较（equal）、大小比较（rel）、加法运算（add）、乘法运算（mul）和基础表达式（pri）。

实际语言中还有更多不同的优先级，比如位运算等。而且优先级是能够改变的，比如我们通常会在语法里通过括号来改变计算的优先级。不过这怎么表达成语法规则呢？

其实，我们在最低层，也就是优先级最高的基础表达式（pri）这里，用括号把表达式包裹起来，递归地引用表达式就可以了。这样的话，只要在解析表达式的时候遇到括号，那么就知道这个是最优先的。这样的话就实现了优先级的改变：

1
2

pri -> Id | Literal | (exp)

了解了这些内容之后，到目前为止，你已经会写整套的表达式规则了，也能让公式计算器支持这些规则了。另外，在使用一门语言的时候，如果你不清楚各种运算确切的优先级，除了查阅常规的资料，你还多了一项新技能，就是阅读这门语言的语法规则文件，这些规则可能就是用 BNF 或 EBNF 的写法书写的。

弄明白优先级的问题以后，我们再来讨论一下结合性这个问题。

确保正确的结合性

在上一讲中，我针对算术表达式写的第二个文法是错的，因为它的计算顺序是错的。“2+3+4”这个算术表达式，先计算了“3+4”然后才和“2”相加，计算顺序从右到左，正确的应该是从左往右才对。

**这就是运算符的结合性问题。**什么是结合性呢？同样优先级的运算符是从左到右计算还是从右到左计算叫做结合性。我们常见的加减乘除等算术运算是左结合的，“.”符号也是左结合的。

比如“rectangle.center.x”是先获得长方形（rectangle）的中心点（center），再获得这个点的 x 坐标。计算顺序是从左向右的。那有没有右结合的例子呢？肯定是有的。赋值运算就是典型的右结合的例子，比如“x = y = 10”。

我们再来回顾一下“2+3+4”计算顺序出错的原因。用之前错误的右递归的文法解析这个表达式形成的简化版本的 AST 如下：

根据这个 AST 做计算会出现计算顺序的错误。不过如果我们将递归项写在左边，就不会出现这种结合性的错误。于是我们得出一个规律：对于左结合的运算符，递归项要放在左边；而右结合的运算符，递归项放在右边。

所以你能看到，我们在写加法表达式的规则的时候，是这样写的：

1
2

add -> mul | add + mul

这是我们犯错之后所学到的知识。那么问题来了，大多数二元运算都是左结合的，那岂不是都要面临左递归问题？不用担心，我们可以通过改写左递归的文法，解决这个问题。

消除左递归

我提到过左递归的情况，也指出递归下降算法不能处理左递归。这里我要补充一点，并不是所有的算法都不能处理左递归，对于另外一些算法，左递归是没有问题的，比如 LR 算法。

消除左递归，用一个标准的方法，就能够把左递归文法改写成非左递归的文法。以加法表达式规则为例，原来的文法是“add -> add + mul”，现在我们改写成：

1
2
3
4



add -> mul add'

add' -> + mul add' | ε

文法中，ε（读作 epsilon）是空集的意思。接下来，我们用刚刚改写的规则再次推导一下“2+3+4”这个表达式，得到了下图中左边的结果：

左边的分析树是推导后的结果。问题是，由于 add’的规则是右递归的，如果用标准的递归下降算法，我们会跟上一讲一样，又会出现运算符结合性的错误。我们期待的 AST 是右边的那棵，它的结合性才是正确的。那么有没有解决办法呢？

答案是有的。我们仔细分析一下上面语法规则的推导过程。只有第一步是按照 add 规则推导，之后都是按照 add’规则推导，一直到结束。

如果用 EBNF 方式表达，也就是允许用 * 号和 + 号表示重复，上面两条规则可以合并成一条：

1
2

add -> mul (+ mul)*

写成这样有什么好处呢？能够优化我们写算法的思路。对于 (+ mul)* 这部分，我们其实可以写成一个循环，而不是一次次的递归调用。伪代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10



mul();

while(next token is +){

  mul()

  createAddNode

}

我们扩展一下话题。在研究递归函数的时候，有一个概念叫做**尾递归，**尾递归函数的最后一句是递归地调用自身。

编译程序通常都会把尾递归转化为一个循环语句，使用的原理跟上面的伪代码是一样的。相对于递归调用来说，循环语句对系统资源的开销更低，因此，把尾递归转化为循环语句也是一种编译优化技术。

好了，我们继续左递归的话题。现在我们知道怎么写这种左递归的算法了，大概是下面的样子：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40



private SimpleASTNode additive(TokenReader tokens) throws Exception {

    SimpleASTNode child1 = multiplicative(tokens);  // 应用 add 规则

    SimpleASTNode node = child1;

    if (child1 != null) {

        while (true) {                              // 循环应用 add'

            Token token = tokens.peek();

            if (token != null && (token.getType() == TokenType.Plus || token.getType() == TokenType.Minus)) {

                token = tokens.read();              // 读出加号

                SimpleASTNode child2 = multiplicative(tokens);  // 计算下级节点

                node = new SimpleASTNode(ASTNodeType.Additive, token.getText());

                node.addChild(child1);              // 注意，新节点在顶层，保证正确的结合性

                node.addChild(child2);

                child1 = node;

            } else {

                break;

            }

        }

    }

    return node;

}

修改完后，再次运行语法分析器分析“2+3+4+5”，会得到正确的 AST：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16



Programm Calculator

    AdditiveExp +

        AdditiveExp +

        AdditiveExp +

            IntLiteral 2

            IntLiteral 3

                IntLiteral 4

        IntLiteral 5

这样，我们就把左递归问题解决了。左递归问题是我们用递归下降算法写语法分析器遇到的最大的一只“拦路虎”。解决这只“拦路虎”以后，你的道路将会越来越平坦。

课程小结

今天我们针对优先级、结合性和左递归这三个问题做了更系统的研究。我来带你梳理一下本节课的重点知识：

优先级是通过在语法推导中的层次来决定的，优先级越低的，越先尝试推导。
结合性是跟左递归还是右递归有关的，左递归导致左结合，右递归导致右结合。
左递归可以通过改写语法规则来避免，而改写后的语法又可以表达成简洁的 EBNF 格式，从而启发我们用循环代替右递归。

为了研究和解决这三个问题，我们还特别介绍了语法规则的产生式写法以及 BNF、EBNF 写法。在后面的课程中我们会不断用到这个技能，还会用工具来生成语法分析器，我们提供给工具的就是书写良好的语法规则。

到目前为止，你已经闯过了语法分析中比较难的一关。再增加一些其他的语法，你就可以实现出一个简单的脚本语言了！

一课一思

本节课提到了语法的优先级、结合性。那么，你能否梳理一下你熟悉的语言的运算优先级？你能说出更多的左结合、右结合的例子吗？可以在留言区与大家一起交流。

最后，感谢你的阅读，如果这篇文章让你有所收获，也欢迎你将它分享给更多的朋友。

文章目录