30|后端总结:充分发挥硬件的能力
文章目录
你好,我是宫文学。
后端的工作,主要是针对各种不同架构的 CPU 来生成机器码。在第 8 讲,我已经对编译器在生成代码的过程中,所做的主要工作进行了简单的概述,你现在应该对编译器的后端工作有了一个大致的了解,也知道了后端工作中的关键算法包括指令选择、寄存器分配和指令排序(又叫做指令调度)。
那么今天这一讲,我们就借助在第二个模块中解析过的真实编译器,来总结、梳理一下各种编译器的后端技术,再来迭代提升一下原有的认知,并加深对以下这些问题的理解:
- 首先,在第 8 讲中,我只讲了指令选择的必要性,但对于如何实现指令选择等步骤,我并没有展开介绍。今天这一讲,我就会带你探索一下指令选择的相关算法。
- 其次,关于寄存器分配算法,我们探索过的好几个编译器,比如 Graal、gc 编译器等,采用的都是线性扫描算法,那么这个算法的原理是什么呢?我们一起来探究一下。
- 最后,我们再回到计算机语言设计的主线上来,一起分析一下不同编译器的后端设计,是如何跟该语言的设计目标相匹配的。
OK,我们先来了解一下指令选择的算法。
指令选择算法
回顾一下,我们主要是在Graal和Go 语言的编译器中,分析了与指令选择有关的算法。它们都采用了一种模式匹配的 DSL,只要找到了符合模式的指令组合,编译器就生成一条低端的、对应于机器码的指令。
**那为什么这种算法是有效的呢?这种算法的原理是什么呢?都有哪些不同的算法实现?**接下来,我就给你揭晓一下答案。
我先给你举个例子。针对表达式“a[i]=b”,它是对数组 a 的第 i 个元素赋值。假设 a 是一个整数数组,那么地址的偏移量就是a+4*i,所以,这个赋值表达式用 C 语言可以写成“*(a+4*i)=b”,把它表达成 AST 的话,就是下图所示的样子。其中,赋值表达式的左子树的计算结果,是一个内存地址。

图 1:a[i]=b 的 AST
那么,我们要如何给这个表达式生成指令呢?
如果你熟悉 x86 汇编,你就会知道,上述语句可以非常简单地表达出来,因为 x86 的指令对数组寻址做了优化(参见第 8 讲的内容)。
不过,这里为了让你更容易理解算法的原理,我设计了一个新的指令集。这个指令集中的每条指令,都对应了一棵 AST 的子树,我们把它叫做模式树(Pattern Tree)。在有的算法里,它们也被叫做瓦片(Tiling)。对一个 AST 生成指令,就是用这样的模式树或瓦片来覆盖整个 AST 的过程。所以,这样的算法也叫做基于模式匹配的指令生成算法。

图 2:指令集中的指令和对应的模式树
你可以看到,在图 2 中,对于每棵模式树,它的根节点是这个指令产生的结果的存放位置。比如,Load_Const 指令执行完毕以后,常数会被保存到一个寄存器里。这个寄存器,又可以作为上一级 AST 节点的操作数来使用。
图 2 中的指令包含:把常数和内存中的值加载到寄存器、加法运算、乘法运算等。其中有两个指令是特殊设计的,目的就是为了让你更容易理解接下来要探究的各种算法。
第一个指令是 #4(Store_Offset),它把值保存到内存的时候,可以在目的地址上加一个偏移量。你可以认为这是为某些场景做的一个优化,比如你在对象地址上加一个偏移量,就能获得成员变量的地址,并把数值保存到这个地址上。
第二个指令是 #9(Lea),它相当于 x86 指令集中的 Lea 指令,能够计算一个地址值,特别是能够利用间接寻址模式,计算出一个数组元素的地址。它能通过一条指令完成一个乘法计算和一个加法计算。如果你忘记了 Lea 指令,可以重新看看第 8 讲的内容。
基于上述的指令和模式树,我们就可以尝试来做一下模式匹配,从而选择出合适的指令。那么都可以采用什么样的算法呢?
第一个算法,是一种比较幼稚的算法。我们采取深度优先的后序遍历,也就是按照“左子节点 -> 右子节点 -> 父节点”的顺序遍历,针对每个节点去匹配上面的模式。
- 第 1 步,采用模式 #2,把内存中 a 的值,也就是数组的地址,加载到寄存器。因为无论加减乘除等任何运算,都是可以拿寄存器作为操作数的,所以做这个决策是很安全的。
- 第 2 步,同上,采用模式 #1,把常量 4 加载到寄存器。
- 第 3 步,采用模式 #2,把内存中 i 的值加载到寄存器。
- 第 4 步,采用模式 #8,把两个寄存器的值相乘,得到(4*i)的值。
- 第 5 步,采用模式 #5,把两个寄存器的值相加,得到 a+4*i 的值,也就是 a[i] 的地址。
- 第 6 步,采用模式 #2,把内存中 b 的值加载到寄存器。
- 第 7 步,采用模式 #3,把寄存器中 b 的值写入 a[i] 的地址。

图 3:用比较幼稚的算法做模式匹配
最后形成的汇编代码是这样的:
Load_Mem a, R1
Load_Const 4, R2
Load_Mem i, R3
Mul_Reg R2, R3
Add_Reg R3, R1
Load_Mem b, R2
Store R2, (R1)
**这种方法,是自底向上的做树的重写。**它的优点是特别简单,缺点是性能比较差。它一共生成了 7 条指令,代价是 19(3+1+3+4+1+3+4)。
在上述步骤中,我们能看到很多可以优化的地方。比如,4*i 这个子表达式,我们是用了 3 条指令来实现的,总的 Cost 是 1+3+4=8,而如果改成两条指令,也就是使用 Mul_mem 指令,就不用先把 i 加载到寄存器,Cost 可以是 1+6=7。
Load_Const 4, R1
Mul_Mem i, R1
**第二种方法,是类似 Graal 编译器所采用的方法,自顶向下的做模式匹配。**比如,当我们处理赋值节点的时候,算法会尽量匹配更多的子节点。因为一条指令包含的子节点越多,那么通过一条指令完成的操作就越多,从而总的 Cost 就更低。
所以,算法的大致步骤是这样的:
- 第 1 步,在 #3 和 #4 两个模式中做选择的话,选中了 #4 号。
- 第 2 步,沿着 AST 继续所深度遍历,其中 + 号节点第 1 步被处理掉了,所以现在处理变量 a,采用了模式 #2,把变量加载到寄存器。
- 第 3 步,处理 * 节点。这个时候要在 #7 和 #8 之间做对比,最后选择了 #7,因为它可以包含更多的节点。
- 第 4 步,处理常量 4。因为上级节点在这里需要一个寄存器作为操作数,所以我们采用了模式 #1,把常量加载到寄存器。
- 第 5 步,处理变量 b。这里也要把它加载到寄存器,因此采用了模式 #2。
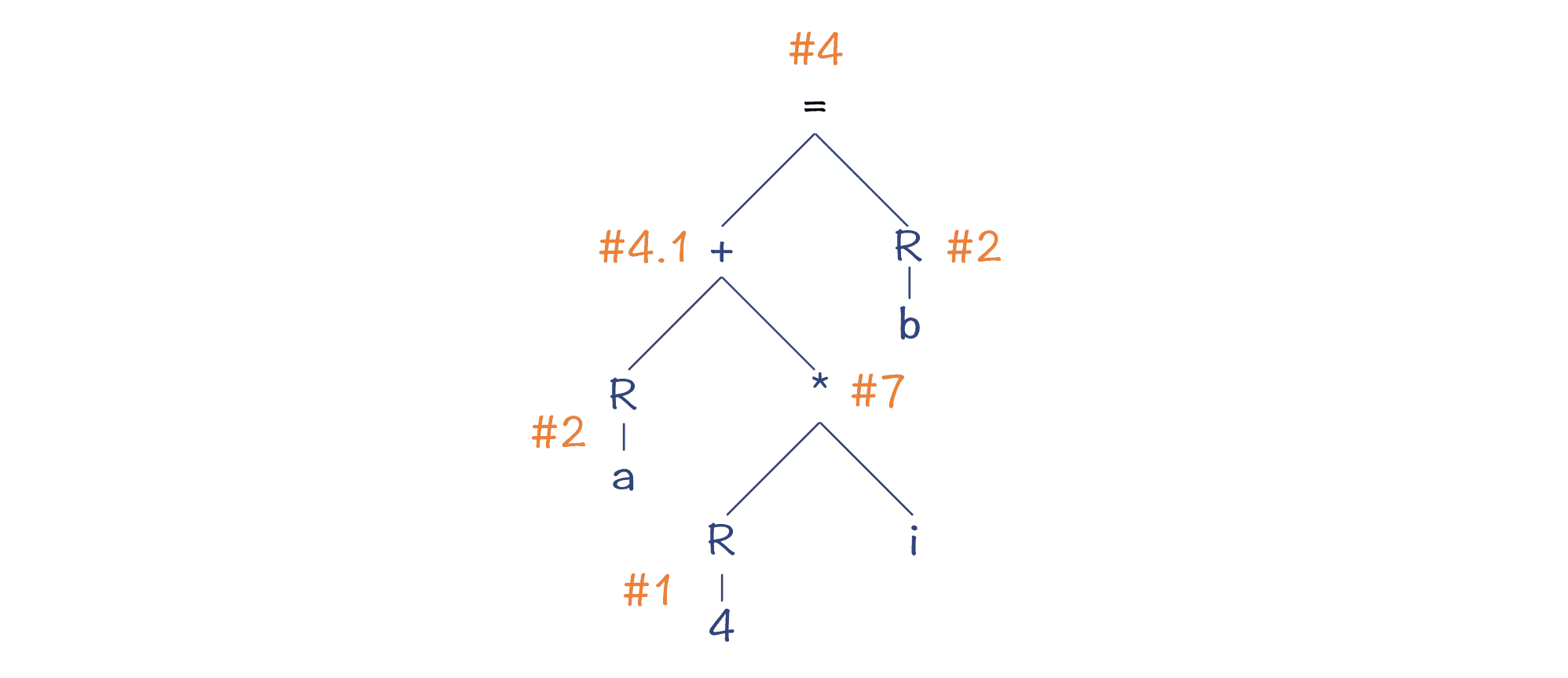
图 4:Maximal Munch 算法的匹配结果
到此为止,我们用了 5 条指令就做完了所有的运算,生成的汇编代码是:
Load_Mem a, R1
Load_Const 4, R2
Mul_Mem R2, i
Load_Mem b, R3
Store_Offset R3, (R1,R2)
这 5 条指令总的 Cost 是 18(3+1+6+3+5)。
上述算法的特点,是在每一步都采用了贪婪策略,这种算法策略有时候也叫做“Maximal Munch”,意思就是每一步都去咬最大的一口。
贪婪策略会生成比幼稚的算法更优化的代码,但它不一定是最优的。你看下图中的匹配策略,它也是用了 5 条指令。

图 5:最优的匹配策略
生成的汇编代码如下:
Lead_Mem a, R1
Load_Mem i, R2
Lea (R1,R2,4), R1
Load_Mem b, R2
Store R2, (R1)
这个新的匹配结果,总的 Cost 是 17(3+3+4+3+4),比前一个算法的结果更优化了。那我们用什么算法能得到这样一个结果呢?
一个思路,是找出用模式匹配来覆盖 AST 的所有可能的模式,并找出其中 Cost 最低的。你可以采用暴力枚举的方法,在每一个节点,去匹配所有可能的模式,从而找出多组解。但显然,这种算法的计算量太大,所需的时间会根据 AST 的大小呈指数级上升,导致编译速度无法接受。
所以我们需要找到一个代价更低的算法,这就是 BURS 算法,也就是“自底向上重写系统,Bottom-Up Rewriting System”。在HotSpot 的 C2 编译器中,就采用了 BURS 算法。这个算法采用了动态规划(Dynamic Programming)的数学方法来获取最优解,同时保持了较低的算法复杂度。
**那么,要想理解 BURS 算法,你就必须要弄懂动态规划的原理。**如果你之前没有学过这个数学方法,请不要紧张,因为动态规划的原理其实是相当简单的。
我在网上发现了一篇能够简洁地说清楚动态规划的文章。它举了一个例子,用最少张的纸币,来凑出某个金额。
比如说,假设你要凑出 15 元,怎么做呢?你还是可以继续采用贪婪算法。首先,拿出一张 10 元的纸币,也就是小于 15 的最大金额,然后再拿出 5 元来。这样你用两张纸币就凑出了 15 这个数值。这个时候,贪婪策略仍然是有效的。
但是,如果某个奇葩的国家发行的货币,不是按照中国货币的面额,而是发行 1、5、11 元三种面额的纸币。那么如果你仍然使用贪婪策略,一开始拿出一张 11 元的纸币,你就还需要再拿出 4 张 1 元的,这样就一共需要 5 张纸币。
但这显然不是最优解。最优解是只需要三张 5 元的纸币就可以了,这就像我们用贪婪算法去做指令生成,得到的可能不是最优解,是同样的道理。
那如何采用动态规划的方法来获取最优解呢?它的思路是这样的,假设我们用 f(n) 来代表凑出 n 元钱最少的纸币数,那么:
- 当一开始取 11 元的话,Cost = f(4) + 1;
- 当一开始取 5 元的话,Cost = f(10) + 1;
- 当一开始取 1 元的话,Cost = f(14) + 1。
所以,我们只需要知道 f(4)、f(10) 和 f(14) 哪个值最小就行了。也就是说,f(15)=min(f(4), f(10), f(14)) + 1。而 f(4)、f(10) 和 f(14) 三个值,也可以用同样的方法递归地求出来,最后得到的值分别是 4、2、4。所以 f(15)=3,这就是最优解。
这个算法最棒的一点,是整个计算中会遇到的 f(14)、f(13)、f(12)、f(11) … f(3)、f(2) 这些值,一旦计算过一遍,就可以缓存下来,不必重复计算,从而让算法的复杂性降低。
所以,动态规划的特点,是通过子问题的最优解,得到总的问题的最优解。这种方法,也可以用于生成最优的指令组合。比如,对于示例程序来说,假设 f(=) 是以赋值运算符为根节点的 AST 所生成的指令的总的最低 Cost,那么:
- 当采用 #3 的时候,Cost = 4 + f(+) + f(b);
- 当采用 #4 的时候,Cost = 5 + f(a) + f(*) + f(b)。
所以你能看出,通过动态规划方法,也能像凑纸币一样,求出树覆盖的最优解。
BURS 算法在具体执行的时候,需要进行三遍的扫描。
第一遍扫描是自底向上做遍历,也就是后序遍历,识别出每个节点可以进行的转换。我在图 6 中给你标了出来。以 a 节点为例,我们可以对它做两个操作,第一个操作是保持一个 mem 节点不动,第二个操作是按照模式 #1 把它转换成一个 reg 节点。

图 6:识别 AST 的每个节点可以进行的转换
第二遍扫描是自顶向下的,运用动态规划的方法找出最优解。
第三遍扫描又是自底向上的,用于生成指令。
好了,那么到目前为止,你就已经了解了指令生成的算法思路了。这里我再补充几点说明:
- 示例中的指令和 Cost 值,是为了便于你理解算法而设计的。在这个示例中,最优解和最差解的 Cost 只差了 2,也就是大约 12% 的性能提升。而在实际应用中,优化力度往往会远远大于这个值。
- 在第 6 讲探究 IR 的数据结构时,我提到过有向无环图(DAG),它比起刚才例子中用到的树结构,能够消除一些冗余的子树,从而减少生成的代码量。LLVM 里在做指令选择的时候,就是采用了 DAG,但算法思路是一样的。
- 示例中到的两个算法,贪婪算法和 BURS 算法,它们花费的时间都与节点数呈线性关系,所以性能都是很高的。其中 BURS 算法的线性系数更大一点,做指令选择所需的时间也更长一点。
OK,那么接下来,我们来探究第二个算法,寄存器分配算法。
寄存器分配算法
在解析 Graal 编译器和 Go 的编译器的时候,我都提到过它们的寄存器分配算法是线性扫描算法。我也提到过,线性扫描算法的性能比较高。
**那么,线性扫描算法的原理是什么呢?**总的来说,线性扫描算法理解起来其实相当简单。我用一个例子来带你了解下。
假设我们的程序里有从 a 到 g 共 7 个变量。通过数据流分析中的变量活跃性分析,你其实可以知道每个变量的生存期。现在,我们已知有 4 个物理寄存器可用,那么我们来看一下要怎么分配这几个物理寄存器。
在第 1 个时间段,a、b、c 和 d 是活跃的,那我们刚好把 4 个物理寄存器分配给这四个变量就行了。

在第 2 个时间段,a 的生存期结束,而一个新的变量 e 变得活跃,那么我们就把 a 原来占用的寄存器刚好给到 e 就可以了。
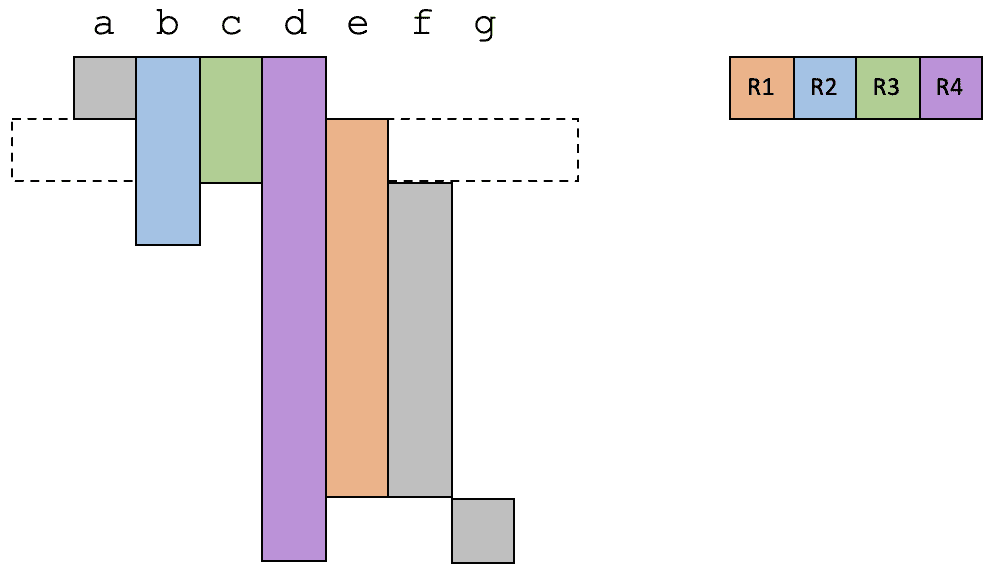
在第 3 个时间段,我们把 c 占用的寄存器给到 f,目前仍然是使用 4 个寄存器。

在第 4 个时间段,b 的生存期结束。这时候只需要用到 3 个寄存器。

在最后一个时间段,只有变量 d 和 g 是活跃的,占用两个寄存器。
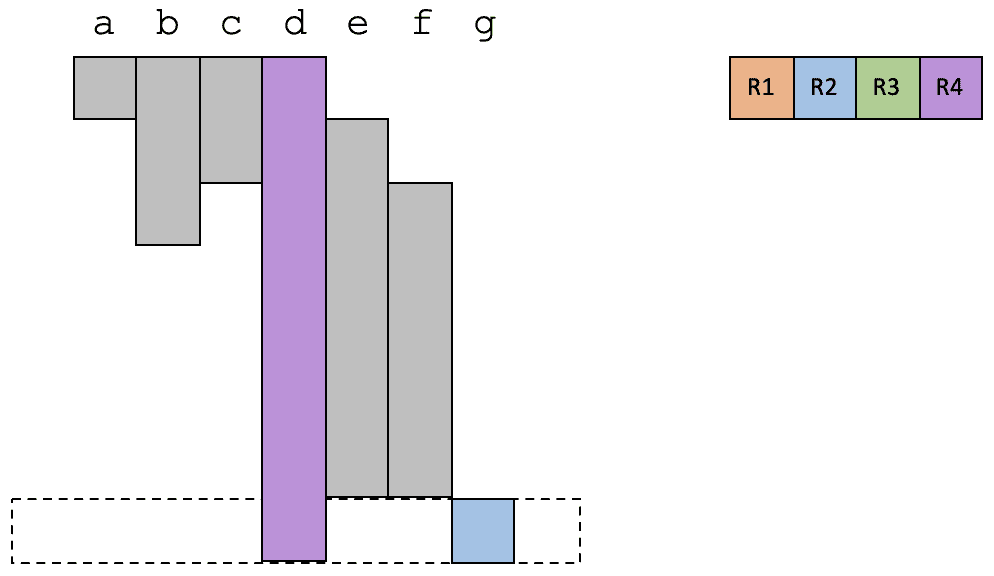
可以看到,在上面这个例子中,所有的变量都可以分配到物理寄存器。而且你也会发现,这个例子中存在多个变量因为生存期是错开的,因此也可以共享同一个寄存器。
但是,如果没有足够的物理寄存器的话,我们要怎么办呢?那就需要把某个变量溢出到内存里了。也就是说,当用到这个变量的时候,才把这个变量加载到寄存器,或者有一些指令可以直接用内存地址作为操作数。
给你举另一个例子,我们来看看物理寄存器不足的情况会是什么样子。在这个例子中,我们有三个物理寄存器。
在第 1 个时间段,物理寄存器是够用的。

在第 2 个时间段,变量 d 变得活跃,现在有 4 个活跃变量,所以必须选择一个溢出到内存。我们选择了 a。
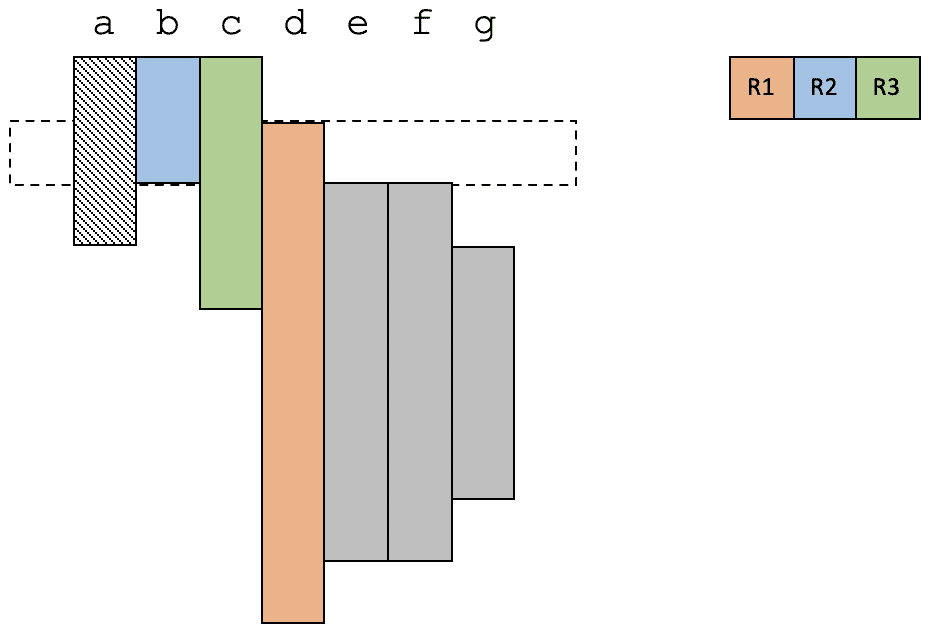
在第 3 个时间段,e 和 f 变得活跃,现在又需要溢出一个变量才可以。这次选择了 c。
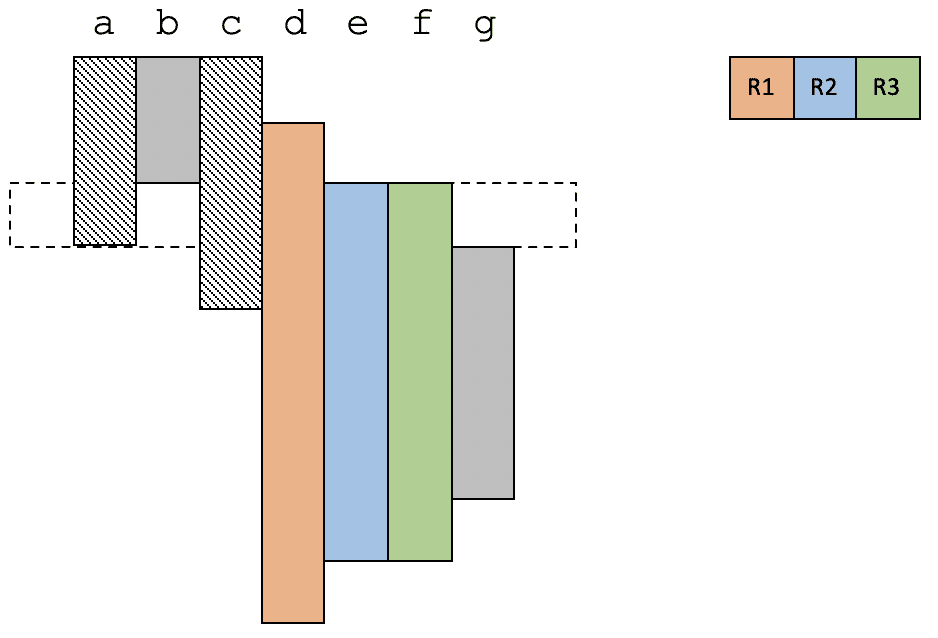
在第 4 个时间段,g 也变得活跃,这次把 d 溢出了。

以上就是**线性扫描算法的思路:线性扫描整个代码,并给活跃变量分配寄存器。如果物理寄存器不足,那么就选择一个变量,溢出到内存中。**你看,是不是很简单?
在掌握了线性扫描算法的思路以后,我再给你补充一点信息:
- 第一,线性扫描算法并不能获得寄存器分配的最优解。所谓最优解,是要让尽量多的操作在寄存器上实现,尽量少地访问内存。因为线性扫描算法并没有去确定一个最优值的目标,所以也就谈不上最优解。
- 第二,线性扫描算法可以采用一些策略,让一些使用频率低的变量被溢出,而像高频使用的循环中的变量,就保留在寄存器里。
- 第三,还有一些其他提升策略。比如,当存在多余的物理寄存器以后,还可以把之前已经溢出的变量重新复活到寄存器里。
好了,上述就是线性扫描的寄存器分配算法。另外我们再来复习一下,在第 8 讲中,我还提到了另一个算法,是图染色算法,这个算法的优化效果更好,但是计算量比较大,会影响编译速度。
接下来,让我们再回到计算机语言设计的主线上,一起讨论一下编译器的后端与语言设计的关系。
编译器后端与语言的设计
编译器后端的目的,是要能够针对不同架构的硬件来生成目标代码,并尽量发挥硬件的能力。那么为了更好地支持语言的设计,在编译器后端的设计上,我们需要考虑到三个方面的因素。
- 平衡编译速度和优化效果
通常,我们都希望编译后的代码越优化越好。但是,在有些场景下,编译速度也很重要。比如像 JVM 这样需要即时编译的运行时环境,编译速度就比较重要。这可能就是 Graal 的指令选择算法和编译器分配算法都比较简单的原因吧。
Go 语言一开始也把编译速度作为一个重要的设计考虑,所以它的后端算法也比较简单。我估计是因为 Go 语言的发起者(Robert Griesemer、Rob Pike 和 Ken Tompson)都具有 C 和 C++ 的背景,甚至 Ken Tompson 还是 C 语言的联合发明人,他们都深受编译速度慢之苦。类似浏览器、操作系统这样比较大的软件,即使是用很多台机器做编译,还是需要编译很久。这可能也是他们为什么想让 Go 的编译速度很快的原因。
而 Julia 的设计目标是用于科学计算的,所以其使用场景主要就是计算密集型的。Julia 采用了 LLVM 做后端,做了比较高强度的优化,即使会因此导致运行时由于 JIT 而引起短暂停顿。
- 确定所支持的硬件平台
确定了一门语言主要运行在什么平台上,那么首先就要支持该平台上的机器码。由于 Go 语言主要是用于写服务端程序的,而服务端采用的架构是有限的,所以 Go 语言支持的架构也是有限的。
硬件平台也影响算法的选择,比如现在很多 CPU 都支持指令的乱序执行,那你在实现编译器的时候就可以省略指令重排序(指令调度)功能。
- 设计后端 DSL
虽然编译器后端要支持多种硬件,但我们其实会希望算法是通用的。所以,各个编译器通常会提供一种 DSL,去描述硬件的特征,从而自动生成针对这种硬件的代码。
在 Graal 中,我们看到了与指令选择有关的注解,在 Go 的编译器中,我们也看到了对 IR 进行转换的 DSL,而 LLVM 则提供了类似的机制。
课程小结
今天这一讲,我把后端的两个重要的算法拿出来给你单独介绍了一下,并一起讨论了后端技术策略与计算机语言的关系。你需要记住这几个知识点:
- 关于指令选择:从 IR 生成机器码(或 LIR),通常是 AST 或 DAG 中的多个节点对应一条指令,所以你要找到一个最佳的组合,把整个 AST 或 DAG 覆盖住,并且要找到一个较优的或最优的解。其中,你还要熟悉贪婪算法和动态规划这两种不同的算法策略,这两种算法不仅仅会用于指令选择,还会用于多种场景。理解了这两种算法之后,就会给你的工具库添加两个重要的工具。
- 关于寄存器分配:线性扫描算法比较简单。不过在一些技术点上我们去深入挖掘一下,其实会发现还挺有意思的。比如,当采用 SSA 格式的 IR 的时候,寄存器分配算法会有什么不同,等等。你可以参考看看文末我给出的资料。
- 关于编译器后端的设计:我们要考虑编译速度和优化程度的平衡,要考虑都能支持哪些硬件。因为要支持多种硬件,通常要涉及后端的 DSL,以便让算法尽量中立于具体的硬件架构。
我把本讲的知识点也整理成了思维导图,供你复习和参考:
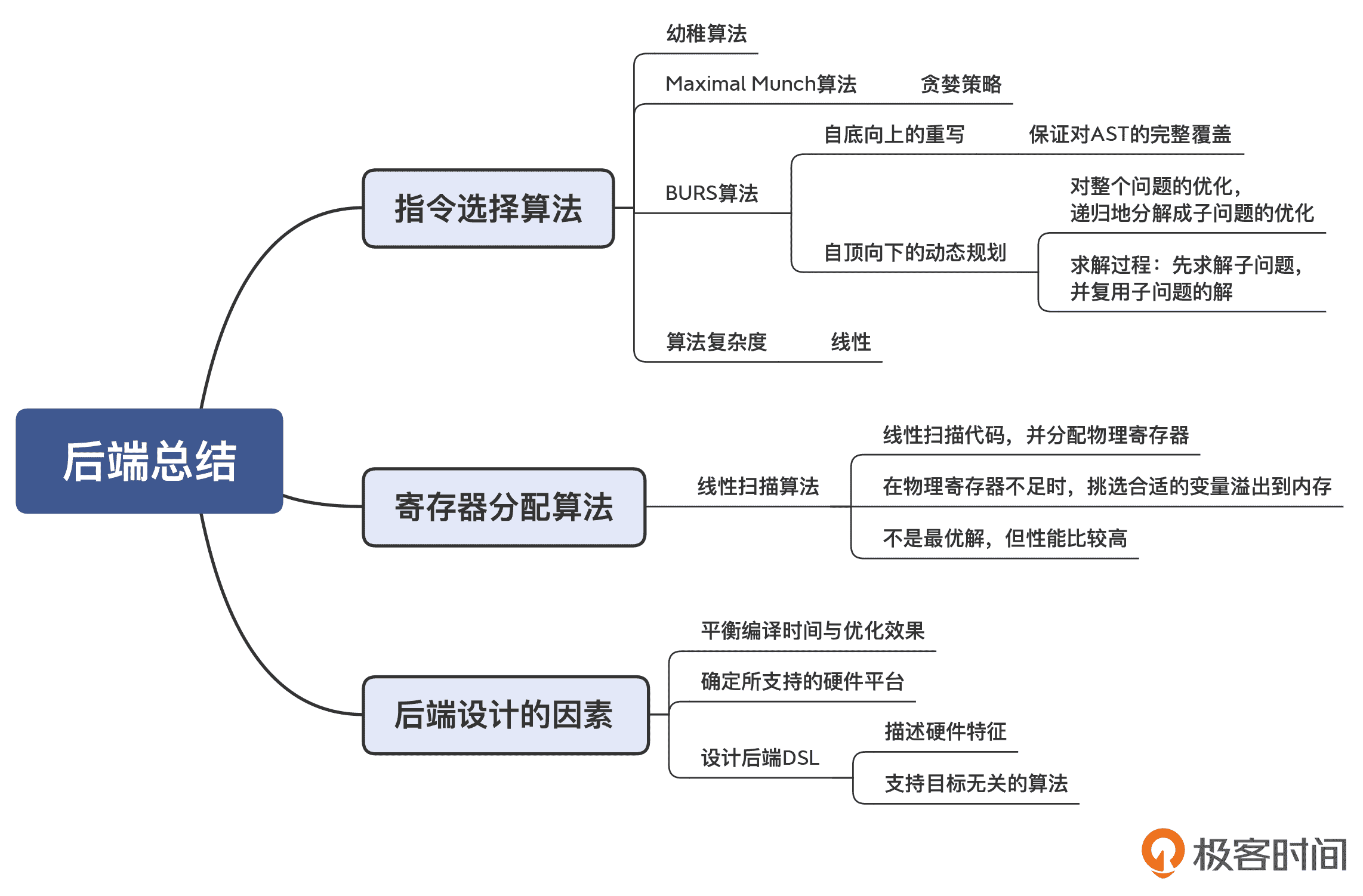
一课一思
动态规划算法是这节课的一个重要知识点。在学过了这个知识点以后,你能否发现它还可以被用于解决哪些问题?欢迎分享你的经验和看法。
参考资料
- 对动态规划方法的理解,我建议你读一下这篇文章,通俗易懂。
- 在《编译原理之美》的第 29 讲,有对寄存器分配算法中的图染色算法的介绍,你可以去参考一下。
- 这两篇关于线性扫描算法的经典论文,你可以去看一下:论文 1,论文 2。
- 这篇文章介绍了针对SSA 格式的 IR 的线性扫描算法,值得一看。
文章作者 anonymous
上次更新 2024-04-06