16|如何使用噪声生成复杂的纹理?
文章目录
你好,我是月影。
在第 11 节课中,我们使用随机技巧生成噪点、迷宫等复杂图案。它们的作用都是表达数据和增强视觉效果。要想在可视化视觉呈现中实现更加酷炫的视觉效果,我们经常需要生成能够模拟大自然的、丰富而复杂的纹理图案。
那么这节课,我们就继续来讨论,如何使用随机技巧来生成更加复杂的纹理图案。
什么是噪声?
我们先来回忆一下,随机效果是怎么生成的。在第 11 节课中,我们使用一个离散的二维伪随机函数,随机生成了一片带有噪点的图案。代码和最终效果如下:
float random (vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))*
43758.5453123);
}

然后,我们用取整的技巧,将这个图案局部放大,就呈现出了如下的方格状图案:
在真实的自然界中,这种离散的随机是存在的,比如鸟雀随机地鸣叫,蝉鸣随机地响起再停止,雨滴随机地落在某个位置等等。但随机和连续并存是更常见的情况,比如山脉的走向是随机的,山峰之间的高度又是连续,类似的还有天上的云朵、水流的波纹、被侵蚀的土地等等。

因此,要模拟这些真实自然的图形,我们就需要把随机和连续结合起来,这样就形成了噪声(Noise)。
如何实现噪声函数?
随机和连续究竟是怎么合成的呢?换句话说,噪声函数是怎么实现的呢?
因为随机数是离散的,那如果我们对离散的随机点进行插值,可以让每个点之间的值连续过渡。因此,我们用 smoothstep 或者用平滑的三次样条来插值,就可以形成一条连续平滑的随机曲线。
下面,我们就通过生成折线的小例子来验证一下。代码如下:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
// 随机函数
float random (float x) {
return fract(sin(x * 1243758.5453123));
}
void main() {
vec2 st = vUv - vec2(0.5);
st *= 10.0;
float i = floor(st.x);
float f = fract(st.x);
// d 直接等于随机函数返回值,这样 d 不连续
float d = random(i);
// float d = mix(random(i), random(i + 1.0), f);
// float d = mix(random(i), random(i + 1.0), smoothstep(0.0, 1.0, f));
// float d = mix(random(i), random(i + 1.0), f * f * (3.0 - 2.0 * f));
gl_FragColor.rgb = (smoothstep(st.y - 0.05, st.y, d) - smoothstep(st.y, st.y + 0.05, d)) * vec3(1.0);
gl_FragColor.a = 1.0;
}
首先,我们对 floor(st.x) 取随机数,取出 10 个不同的 d 值,然后把它们绘制出来,就能在画布上呈现出 10 段不连续的线段。

然后,我们用 mix(random(i), random(i + 1.0), f); 替换 random(i)(你可以将上面代码第 18 行注释掉,将第 19 行注释去掉),那么这些线段的首尾就会连起来,也就是说我们将得到一段连续的折线。
不过,我们得到的折线虽然连续,但因为这个函数在端点处不可导,所以它不平滑。因此,我们可以改用 mix(random(i), random(i + 1.0), smoothstep(0.0, 1.0, f)); 替换 random(i)(上面代码的第 20 行),或者直接采用三次多项式 mix(random(i), random(i + 1.0), f * f * (3.0 - 2.0 * f));(上面代码的第 21 行,这个三次多形式能达到和 smoothstep 一样的效果)来替换 step。这样,我们就得到一条连续并且平滑的曲线了。
这也就是我们想要的噪声函数了。
但是,这个函数是一维的,如果要使用二维的,我们还可以把它扩展到二维。这个时候,我们就必须要知道,二维噪声和一维噪声之间的区别。很明显,一维噪声是对两点进行插值的,而二维噪声需要对平面画布上方形区域的四个顶点,分别从 x、y 方向进行两次插值。
图片来源:The Book of Shaders
具体怎么做呢?我们可以把 st 与方形区域的四个顶点(对应四个向量)做插值,这样就能得到二维噪声。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
float random (vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))*
43758.5453123);
}
// 二维噪声,对 st 与方形区域的四个顶点插值
highp float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f * f * (3.0 - 2.0 * f);
return mix( mix( random( i + vec2(0.0,0.0) ),
random( i + vec2(1.0,0.0) ), u.x),
mix( random( i + vec2(0.0,1.0) ),
random( i + vec2(1.0,1.0) ), u.x), u.y);
}
void main() {
vec2 st = vUv * 20.0;
gl_FragColor.rgb = vec3(noise(st));
gl_FragColor.a = 1.0;
}
通过上面的代码,我们就可以得到下面这个看起来比较模糊的噪声图案。

模糊的噪声图案
噪声的应用
那你可能想问了,我们上面实现的一维噪声波形和二维的模糊噪声图案都比较简单,那它们到底是怎么模拟自然界中的现象,又该怎么实现有趣的视觉效果呢?
接下来,我们先结合上面得到的噪声函数,来讲 2 个简单的噪声应用,让你对它们能有更具体的认知。然后,我会在此基础上,再讲一些其他噪声函数,以及噪声能实现的更复杂视觉效果,让你对噪声有更深入的理解。
首先,我们可以结合噪声和距离场,来实现类似于水滴滚过物体表面的效果。
void main() {
vec2 st = mix(vec2(-10, -10), vec2(10, 10), vUv);
float d = distance(st, vec2(0));
d *= noise(uTime + st);
d = smoothstep(0.0, 1.0, d) - step(1.0, d);
gl_FragColor.rgb = vec3(d);
gl_FragColor.a = 1.0;
}
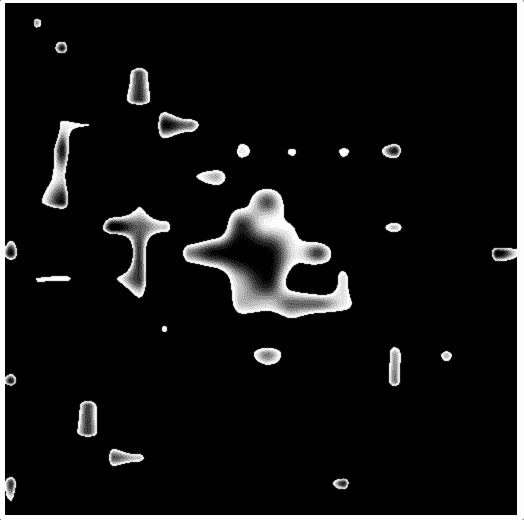
我们也可以使用不同的距离场构造方式,加上旋转噪声,构造出类似于木头的条纹。代码如下:
float lines(in vec2 pos, float b){
float scale = 10.0;
pos *= scale;
return smoothstep(0.0, 0.5 + b * 0.5, abs((sin(pos.x * 3.1415) + b * 2.0)) * 0.5);
}
vec2 rotate(vec2 v0, float ang) {
float sinA = sin(ang);
float cosA = cos(ang);
mat3 m = mat3(cosA, -sinA, 0, sinA, cosA, 0, 0, 0, 1);
return (m * vec3(v0, 1.0)).xy;
}
void main() {
vec2 st = vUv.yx * vec2(10.0, 3.0);
st = rotate(st, noise(st));
float d = lines(st, 0.5);
gl_FragColor.rgb = 1.0 - vec3(d);
gl_FragColor.a = 1.0;
}

这两个应用的实现代码非常简单,你直接看代码就能理解。我更希望的是,你能通过我给出的代码,来理解这种噪声结合距离场的实现思路。
梯度噪声
我们前面说的噪声算法,它的原理是对离散的随机值进行插值,因此它又被称为插值噪声(Value Noise)。插值噪声有一个缺点,就是它的值的梯度不均匀。最直观的表现就是,二维噪声图像有明显的“块状”特点,不够平滑。
想要解决这个问题,我们可以使用另一种噪声算法,也就是梯度噪声(Gradient Noise)。梯度噪声是对随机的二维向量来插值,而不是一维的随机数。这样我们就能够获得更加平滑的噪声效果。梯度噪声的代码如下:
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
vec2 random2(vec2 st){
st = vec2( dot(st,vec2(127.1,311.7)),
dot(st,vec2(269.5,183.3)) );
return -1.0 + 2.0 * fract(sin(st) * 43758.5453123);
}
// Gradient Noise by Inigo Quilez - iq/2013
// https://www.shadertoy.com/view/XdXGW8
float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f * f * (3.0 - 2.0 * f);
return mix( mix( dot( random2(i + vec2(0.0,0.0) ), f - vec2(0.0,0.0) ),
dot( random2(i + vec2(1.0,0.0) ), f - vec2(1.0,0.0) ), u.x),
mix( dot( random2(i + vec2(0.0,1.0) ), f - vec2(0.0,1.0) ),
dot( random2(i + vec2(1.0,1.0) ), f - vec2(1.0,1.0) ), u.x), u.y);
}
void main() {
vec2 st = vUv * 20.0;
gl_FragColor.rgb = vec3(0.5 * noise(st) + 0.5);
gl_FragColor.a = 1.0;
}
梯度噪声可以平滑到什么程度呢?我在下面给出了两种噪声算法生成的图像,你可以明显得看出对比。第一个图是插值噪声的效果,黑白色之间过渡不够平滑,还有明显的色块感,第二个图是梯度噪声的效果,黑白的过渡就明显平滑多了,不再呈现块状。
插值噪声与梯度噪声对比
因此,梯度噪声在二维空间中的应用更广泛,许多有趣的模拟自然界特效的视觉实现都采用了梯度噪声。你可以研究一下Shadertoy.com平台上的一些例子,其中很多模拟自然界的例子都和梯度噪声有关,我就不一一列举了。
用噪声实现云雾效果
我还想给你讲一种使用噪声来模拟云雾效果的方法。如果你看过极客时间里 winter 老师的《重学前端》,可能对这个方法有所了解,因为他在一篇加餐简单提到过。在这里,我想给你详细说说云雾效果究竟是怎么实现的。
我们可以通过改变噪声范围,然后按照不同权重来叠加的方式创造云雾效果。比如,我们可以将噪声叠加 6 次,然后让它每次叠加的时候范围扩大一倍,但是权重减半。通过这个新的噪声算法,我们就能生成云雾效果了。你也可以试试,让这个噪声配合色相变化,可以创造出非常有趣的图形,比如模拟飞机航拍效果。
//
#define OCTAVES 6
float mist(vec2 st) {
//Initial values
float value = 0.0;
float amplitude = 0.5;
// 叠加 6 次
for(int i = 0; i < OCTAVES; i++) {
// 每次范围扩大一倍,权重减半
value += amplitude * noise(st);
st *= 2.0;
amplitude *= 0.5;
}
return value;
}
//配合色相的变化
void main() {
vec2 st = vUv;
st.x += 0.1 * uTime;
gl_FragColor.rgb = hsb2rgb(vec3 (mist(st), 1.0, 1.0));
gl_FragColor.a = 1.0;
}
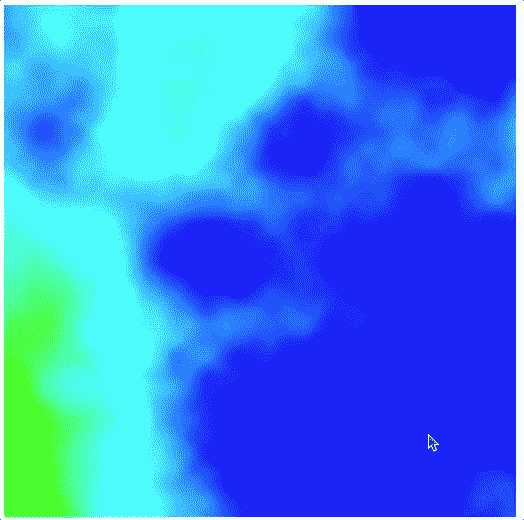
使用云雾效果生成的图案,非常像是飞机航拍
Simplex Noise
接下来,我还想给你讲一种更新的噪声算法,它是 Ken Perlin 在 2001 年的 Siggraph 会议上展示的 Simplex Noise 算法。
相比于前面的噪声算法,Simplex Noise 算法有更低的计算复杂度和更少的乘法运算,并且可以用更少的计算量达到更高的维度,而且它制造出的噪声非常自然。
Simplex Noise 与插值噪声以及梯度噪声的不同之处在于,它不是对四边形进行插值,而是对三角网格进行插值。与四边形插值相比,三角网格插值需要计算的点更少了,这样自然大大降低了计算量,从而提升了渲染性能。
Simplex Noise 具体的实现思路非常精巧和复杂,其中包含的数学技巧比较高深,这里我就不详细来讲了,如果你有兴趣学习可以参考Book of Shaders 的文章来学习。
尽管 Simplex Noise 的原理很巧妙和复杂,但是在 Shader 中实现 Simplex Noise 代码并不算太复杂,你可以记住下面的代码,在需要的时候直接拿来使用。
vec3 mod289(vec3 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec2 mod289(vec2 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec3 permute(vec3 x) { return mod289(((x*34.0)+1.0)*x); }
//
// Description : GLSL 2D simplex noise function
// Author : Ian McEwan, Ashima Arts
// Maintainer : ijm
// Lastmod : 20110822 (ijm)
// License :
// Copyright (C) 2011 Ashima Arts. All rights reserved.
// Distributed under the MIT License. See LICENSE file.
// https://github.com/ashima/webgl-noise
//
float noise(vec2 v) {
// Precompute values for skewed triangular grid
const vec4 C = vec4(0.211324865405187,
// (3.0-sqrt(3.0))/6.0
0.366025403784439,
// 0.5*(sqrt(3.0)-1.0)
-0.577350269189626,
// -1.0 + 2.0 * C.x
0.024390243902439);
// 1.0 / 41.0
// First corner (x0)
vec2 i = floor(v + dot(v, C.yy));
vec2 x0 = v - i + dot(i, C.xx);
// Other two corners (x1, x2)
vec2 i1 = vec2(0.0);
i1 = (x0.x > x0.y)? vec2(1.0, 0.0):vec2(0.0, 1.0);
vec2 x1 = x0.xy + C.xx - i1;
vec2 x2 = x0.xy + C.zz;
// Do some permutations to avoid
// truncation effects in permutation
i = mod289(i);
vec3 p = permute(
permute( i.y + vec3(0.0, i1.y, 1.0))
+ i.x + vec3(0.0, i1.x, 1.0 ));
vec3 m = max(0.5 - vec3(
dot(x0,x0),
dot(x1,x1),
dot(x2,x2)
), 0.0);
m = m*m ;
m = m*m ;
// Gradients:
// 41 pts uniformly over a line, mapped onto a diamond
// The ring size 17*17 = 289 is close to a multiple
// of 41 (41*7 = 287)
vec3 x = 2.0 * fract(p * C.www) - 1.0;
vec3 h = abs(x) - 0.5;
vec3 ox = floor(x + 0.5);
vec3 a0 = x - ox;
// Normalise gradients implicitly by scaling m
// Approximation of: m *= inversesqrt(a0*a0 + h*h);
m *= 1.79284291400159 - 0.85373472095314 * (a0*a0+h*h);
// Compute final noise value at P
vec3 g = vec3(0.0);
g.x = a0.x * x0.x + h.x * x0.y;
g.yz = a0.yz * vec2(x1.x,x2.x) + h.yz * vec2(x1.y,x2.y);
return 130.0 * dot(m, g);
}
void main() {
vec2 st = vUv * 20.0;
gl_FragColor.rgb = vec3(0.5 * noise(st) + 0.5);
gl_FragColor.a = 1.0;
}
渲染效果如下图:

Simplex Noise 可以实现出令人惊叹的效果,在Shadertoy.com平台上经常有大神分享他们创作的神奇效果。比如,这个像某种溶洞的岩壁效果,就有一种大自然鬼斧神工的韵味在。

再比如,这种像电影大片中才有的效果,你很难想象这并不是视频,甚至不是图片,只不过是我们用数学公式在 Shader 中计算并绘制出来的图案而已。

网格噪声
最后,我们来讲讲网格噪声。前面我们已经使用过大量网格化的技术,我想你也应该比较熟悉了。那什么是网格噪声呢?它就是将噪声与网格结合使用的一种纹理生成技术。下面,让我们通过一个生成动态生物细胞的例子,来详细理解一下如何使用网格噪声。
首先,我们用网格技术将画布分为 10*10 的网格。然后,我们构建距离场。这个距离场是在每个网格中随机一个特征点,然后计算网格内到该点的距离,最后根据距离来着色。
#ifdef GL_ES
precision highp float;
#endif
varying vec2 vUv;
uniform float uTime;
vec2 random2(vec2 st){
st = vec2( dot(st,vec2(127.1,311.7)),
dot(st,vec2(269.5,183.3)) );
return fract(sin(st) * 43758.5453123);
}
void main() {
vec2 st = vUv * 10.0;
float d = 1.0;
vec2 i_st = floor(st);
vec2 f_st = fract(st);
vec2 p = random2(i_st);
d = distance(f_st, p);
gl_FragColor.rgb = vec3(d);
gl_FragColor.a = 1.0;
}
通过上面的代码,我们最终能得到如下的效果:

我们可以看到,这里的每个网格是独立的,并且界限分明。那如果我们想让它们的边界过渡更圆滑该怎么办呢?我们可以在原来的代码上做改变,具体来说就是不仅计算特征点到当前网格的距离,还要计算它到周围相邻的 8 个网格的距离,然后取最小值。与其他的编程语言类似,这个可以通过 for 循环来实现:
void main() {
vec2 st = vUv * 10.0;
float d = 1.0;
vec2 i_st = floor(st);
vec2 f_st = fract(st);
for(int i = -1; i <= 1; i++) {
for(int j = -1; j <= 1; j++) {
vec2 neighbor = vec2(float(i), float(j));
vec2 p = random2(i_st + neighbor);
d = min(d, distance(f_st, neighbor + p));
}
}
gl_FragColor.rgb = vec3(d);
gl_FragColor.a = 1.0;
}
这里有一点需要注意,GLSL 语言的 for 循环限制比较多。其中,检查循环是否继续的次数必须是常量,不能是变量。所以 GLSL 中没有动态循环,而且迭代的次数必须是确定的。这里我们要检查 9 个网格,所以就用了两重循环来实现。
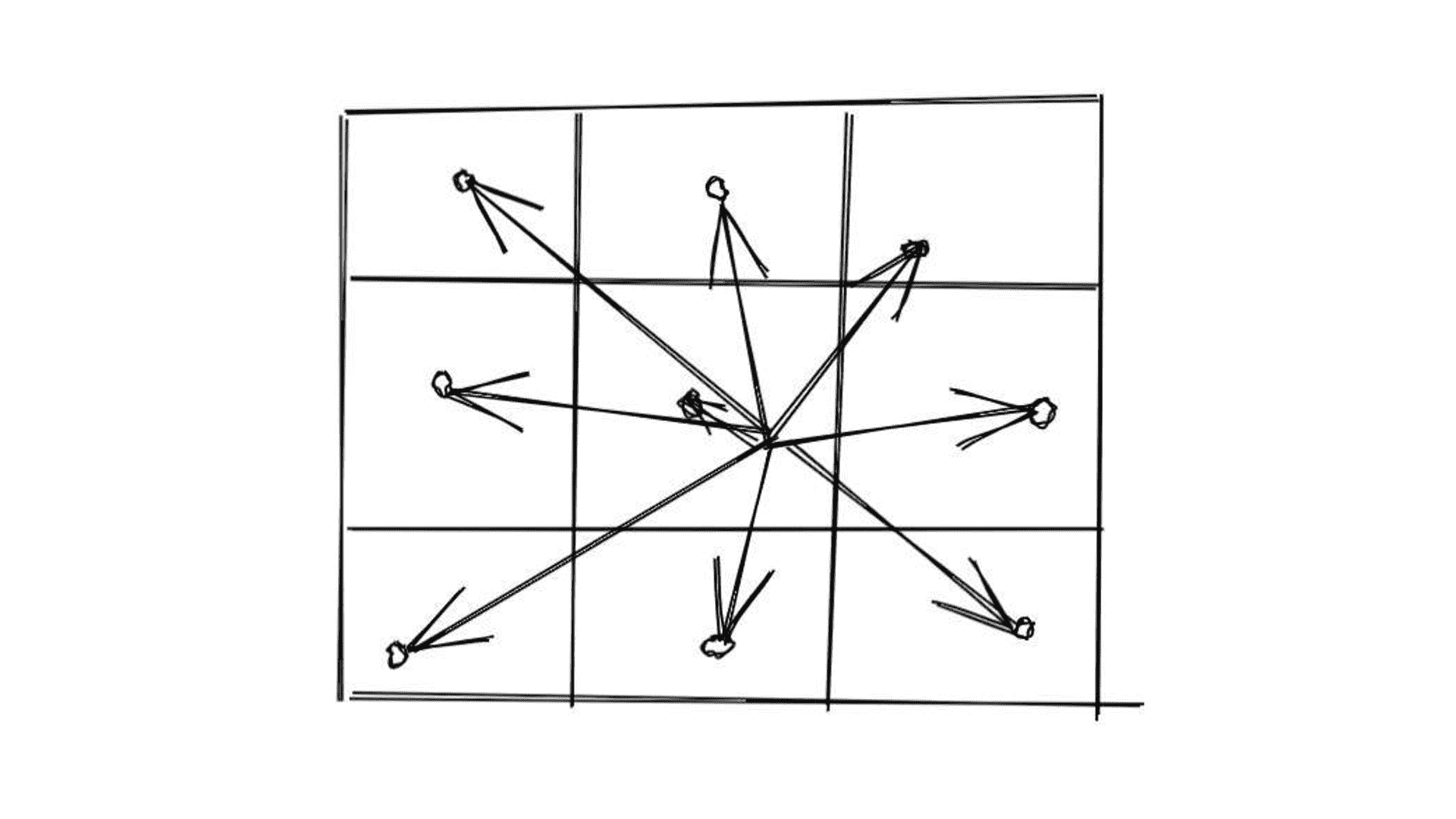
计算像素坐标到九个特征点的最短距离

然后我们加上 uTime,让网格动起来,另外我们把特征点也给显示出来。我们修改一下代码:
void main() {
vec2 st = vUv * 10.0;
float d = 1.0;
vec2 i_st = floor(st);
vec2 f_st = fract(st);
for(int i = -1; i <= 1; i++) {
for(int j = -1; j <= 1; j++) {
vec2 neighbor = vec2(float(i), float(j));
vec2 p = random2(i_st + neighbor);
p = 0.5 + 0.5 * sin(uTime + 6.2831 * p);
d = min(d, distance(f_st, neighbor + p));
}
}
gl_FragColor.rgb = vec3(d) + step(d, 0.03);
gl_FragColor.a = 1.0;
}
这样,最终绘制的效果如下,它就有点像是运动的生物细胞。

网格噪声是一种目前被广泛应用的程序化纹理技术,用来生成随机网格类的视觉效果,可以用来模拟物体表面的晶格、晶体生长、细胞、微生物等等有趣的效果。
网格噪声模拟物体表面晶格,图片来源于 The Book of Shaders
要点总结
总的来说,这节课我给你讲的技术,实际上是一种复杂的程序化纹理生成技术。所谓程序化纹理生成技术,就是用程序来生成物体表面的图案。我们在这些图案中引入类似于自然界中的随机性,就可以模拟出自然的、丰富多采的,以及包含真实细节的纹理图案。
这其中最有代表性的就是噪声了,噪声就是随机性与连续性结合而成的。噪声是自然界中普遍存在的自然规律。模拟噪声的基本思路是对离散的随机数进行平滑处理,对随机数进行平滑处理有不同的数学技巧,所以有插值噪声、梯度噪声、Simplex Noise 等等不同的噪声算法。它们各有特点,我们可以根据不同的情况来选择怎么使用。
这一节课的内容偏向于技巧性,要想掌握好,我建议你多动手实践。我推荐给你一个非常不错的平台,Shadertoy.com 。它是一个非常优秀的创作和分享着色器效果的平台,你可以在上面学习到很多优秀的案例,然后通过代码来理解创作者的创意和思路,巩固今天所学的知识。
小试牛刀
你能试着写出一个 Shader,来实现我在下面给出的网格噪声效果吗?欢迎你把它分享出来。

欢迎在留言区和我讨论,分享你的答案和思考,也欢迎你把这节课分享给你的朋友,我们下节课再见!
源码
完整示例代码见GitHub 仓库
推荐阅读
[1] Shadertoy
[2] The Book of Shaders
文章作者 anonymous
上次更新 2024-02-10

