18|如何生成简单动画让图形动起来?
文章目录
你好,我是月影。
前面,我们用了 3 个模块的时间,学习了大量的图形学和数学知识,是不是让你的脑袋有一点昏沉?没关系,你只是需要一点时间来消化这些知识而已。我能给你的建议就是多思考、多练习,有了时间的积累,你一定可以掌握这些基础知识和思维方法。
从这一节课开始,我们要学习一个非常有意思的新模块,那就是动画和 3D 绘图。对于可视化展现来说,动画和 3D 都是用来强化数据表达,吸引用户的重要技术手段。它们往往比二维平面图形能够表达更复杂的数据,实现更吸引人的视觉效果。
那今天,我们先来聊聊动画的实现。实际上,我们之前也实现了不少动态效果,但你可能还是不知道怎么去实现动画。接下来,我们就来系统地梳理一下动画实现的标准方法。
动画的三种形式
什么是动画呢?简单来说,动画就是将许多帧静止的画面以固定的速率连续播放出来。一般来说,动画有三种形式,分别是固定帧动画、增量动画和时序动画。
第一种形式是我们预先准备好要播放的静态图像,然后将这些图依次播放,所以它叫做固定帧动画。增量动画是在动态绘制图像的过程中,我们修改每一帧中某个或某几个属性的值,给它们一定的增量。第三种形式是在动态绘制图像的过程中,我们根据时间和动画函数计算每一帧中的关键属性值,然后更新这些属性,所以它叫做时序动画。
这么说还是比较抽象,下面,我就以 HTML/CSS 为例,来带你熟悉这三种动画的基本形式。为什么选 HTML/CSS 呢?因为一般来说,HTML/CSS、SVG 和 Canvas2D 实现动画的方式大同小异,所以我就直接选择你最熟悉的 HTML/CSS 了。而 WebGL 实现动画的方式和其他三种图形系统都有差别,所以我会在下一节课单独来说。
1. 实现固定帧动画
首先,我们来说说如何实现固定帧动画。
结合固定帧动画的定义,我们实现它的第一步,就是为每一帧准备一张静态图像。比如说,我们要实现一个循环播放 3 帧的动画,就要准备 3 个如下的图像。

3 个静态图像
第二步,我们要依次播放这些图像。在 CSS 里实现的时候,我们使用图片作为背景,就可以让它们逐帧切换了。代码如下所示:
.bird {
position: absolute;
left: 100px;
top: 100px;
width:86px;
height:60px;
zoom: 0.5;
background-repeat: no-repeat;
background-image: url(https://p.ssl.qhimg.com/t01f265b6b6479fffc4.png);
background-position: -178px -2px;
animation: flappy .5s step-end infinite;
}
@keyframes flappy {
0% {background-position: -178px -2px;}
33% {background-position: -90px -2px;}
66% {background-position: -2px -2px;}
}

动态的小鸟
虽然固定帧动画实现起来非常简单,但它不适合生成需要动态绘制的图像,更适合在游戏等应用场景中,生成由美术提供现成图片的动画帧图像。而对于动态绘制的图像,也就是非固定帧动画,我们通常会使用另外两种方式。
2. 实现增量动画
我们先来说比较简单的增量动画,即每帧给属性一个增量。怎么理解呢?我举个简单的例子,我们可以创建一个蓝色的方块,然后给这个方块的每一帧增加一个 rotate 角度。这样就能实现蓝色方块旋转的动画。具体的代码和效果如下所示。

旋转的蓝色方块
在上面的例子中,我们重点关注第 22 到 26 这 5 行 JavaScript 代码就行了,关键逻辑在于我们修改 rotatation 值,每次绘制的时候将它加 1。这样我们就实现增量动画,是不是也很简单?
确实,增量动画的优点就是实现简单。但它也有 2 个缺点。首先,因为它使用增量来控制动画,从数学角度来说,也就是我们直接使用了一阶导数来定义的动画。这样的绘图方式不太好控制动画的细节,比如动画周期、变化率、轨迹等等,所以这种方法只能用来实现简单动画。
其次,增量动画定义的是状态变化。如果我们要在 shader 中使用动画,就只能采用后期处理通道来实现。但是后期处理通道要进行多次渲染,实现起来比较繁琐,而且性能开销也比较大。所以,更加复杂的轨迹动画,我们一般采用第三种方式,也就是通过定义时间和动画函数来实现。
3. 实现时序动画
还是以旋转的蓝色方块为例,我们改写一下它的 JavaScript 代码。
const block = document.querySelector(’.block’);
const startAngle = 0;
const T = 2000;
let startTime = null;
function update() {
startTime = startTime == null ? Date.now() : startTime;
const p = (Date.now() - startTime) / T;
const angle = startAngle + p * 360;
block.style.transform = rotate(${angle}deg);
requestAnimationFrame(update);
}
update();
首先,我们定义 2 个变量,startAnglehe 和 T。其中,startAnglehe 是起始旋转角度,T 是旋转周期。在第一次调用 update 的时候,我们设置初始旋转的时间为 startTime,那么在每次调用 update 的时候,当前经过的时间就是 Date.now() - startTime。
接着,我们将它除以周期 T,就能得到旋转进度 p,那么当前角度就等于 startAngle + p * 360。然后我们将当前角度设置为元素的 rotate 值,就实现了同样的旋转动画。
总的来说,时序动画的实现可以总结为三步:首先定义初始时间和周期,然后在 update 中计算当前经过时间和进度 p,最后通过 p 来更新动画元素的属性。虽然时序动画实现起来比增量动画写法更复杂,但我们可以更直观、精确地控制旋转动画的周期(速度)、起始角度等参数。
也正因为如此,这种方式在动画实现中最为常用。那为了更方便使用和拓展,我们可以把实现时序动画的三个步骤抽象成标准的动画模型。具体怎么做呢?我们接着往下看。
定义标准动画模型
首先,我们定义一个类 Timing 用来处理时间,具体代码如下:
export class Timing {
constructor({duration, iterations = 1} = {}) {
this.startTime = Date.now();
this.duration = duration;
this.iterations = iterations;
}
get time() {
return Date.now() - this.startTime;
}
get p() {
const progress = Math.min(this.time / this.duration, this.iterations);
return this.isFinished ? 1 : progress % 1;
}
get isFinished() {
return this.time / this.duration >= this.iterations;
}
}
然后,我们实现一个 Animator 类,用来真正控制动画过程。
import {Timing} from ‘./timing.js’;
export class Animator {
constructor({duration, iterations}) {
this.timing = {duration, iterations};
}
animate(target, update) {
let frameIndex = 0;
const timing = new Timing(this.timing);
return new Promise((resolve) => {
function next() {
if(update({target, frameIndex, timing}) !== false && !timing.isFinished) {
requestAnimationFrame(next);
} else {
resolve(timing);
}
frameIndex++;
}
next();
});
}
}
Animator 构造器接受{duration, iterations}作为参数,它有一个 animate 方法,会在执行时创建一个 timing 对象,然后通过执行 update({target, frameIndex, timing}) 更新动画,并且会返回一个 promise 对象。这样,在动画结束时,resolve 这个 promise,我们就能够很方便地实现连续动画了。
接下来,你可以想一个动画效果,来试验一下这个模型的效果。比如说,我们可以用 Animator 实现四个方块的轮换转动,让每个方块转动的周期是 1 秒,一共旋转 1.5 个周期(即 540 度)。代码和效果如下所示。

顺序旋转的四个方块
插值与缓动函数
我们前面说过,时序动画的好处就在于,它能更容易地控制动画的细节。那针对我们总结出的这个标准的动画模型,它又如何控制动画细节呢?
假设,我们已知元素的起始状态、结束状态和运动周期。如果想要让它进行不规则运动,我们可以使用插值的方式来控制每一帧的展现。比如说,我们可以先实现一个匀速运动的方块,再通过插值与缓动函数来实现变速运动。
首先,我们用 Animator 实现一个方块,让它从 100px 处匀速运动到 400px 处。注意,在代码实现的时候,我们使用了一个线性插值方法:left = start * (1 - p) + end * p。线性插值可以很方便地实现属性的均匀变化,所以用它来让方块做匀速运动是非常简单的。但如果是让方块非匀速运动,比如匀加速运动,我们要怎么办呢?
import {Animator} from ‘../common/lib/animator/index.js’;
const block = document.querySelector(’.block’);
const animator = new Animator({duration: 3000});
document.addEventListener(‘click’, () => {
animator.animate({el: block, start: 100, end: 400}, ({target: {el, start, end}, timing: {p}}) => {
const left = start * (1 - p) + end * p;
el.style.left = ${left}px;
});
});
实现技巧也很简单,我们仍然可以使用线性插值,只不过要对插值参数 p 做一个函数映射。比如说,如果要让方块做初速度为 0 的匀加速运动,我们可以将 p 映射为 p^2。
p = p ** 2;
const left = start * (1 - p) + end * p;
再比如说,如果要让它做末速度为 0 的匀减速运动,我们可以将 p 映射为 p * (2 - p)。
p = p * (2 - p);
const left = start * (1 - p) + end * p;
那为什么匀加速、匀减速的时候,p 要这样映射呢?要理解这一点,我们就得先来回忆一下,匀加速和匀减速运动的物理计算公式。
假设,某个物体在做初速度为 0 的匀加速运动,运动的总时间为 T,总位移为 S。那么,它在 t 时刻的位移和加速度的计算公式如下:
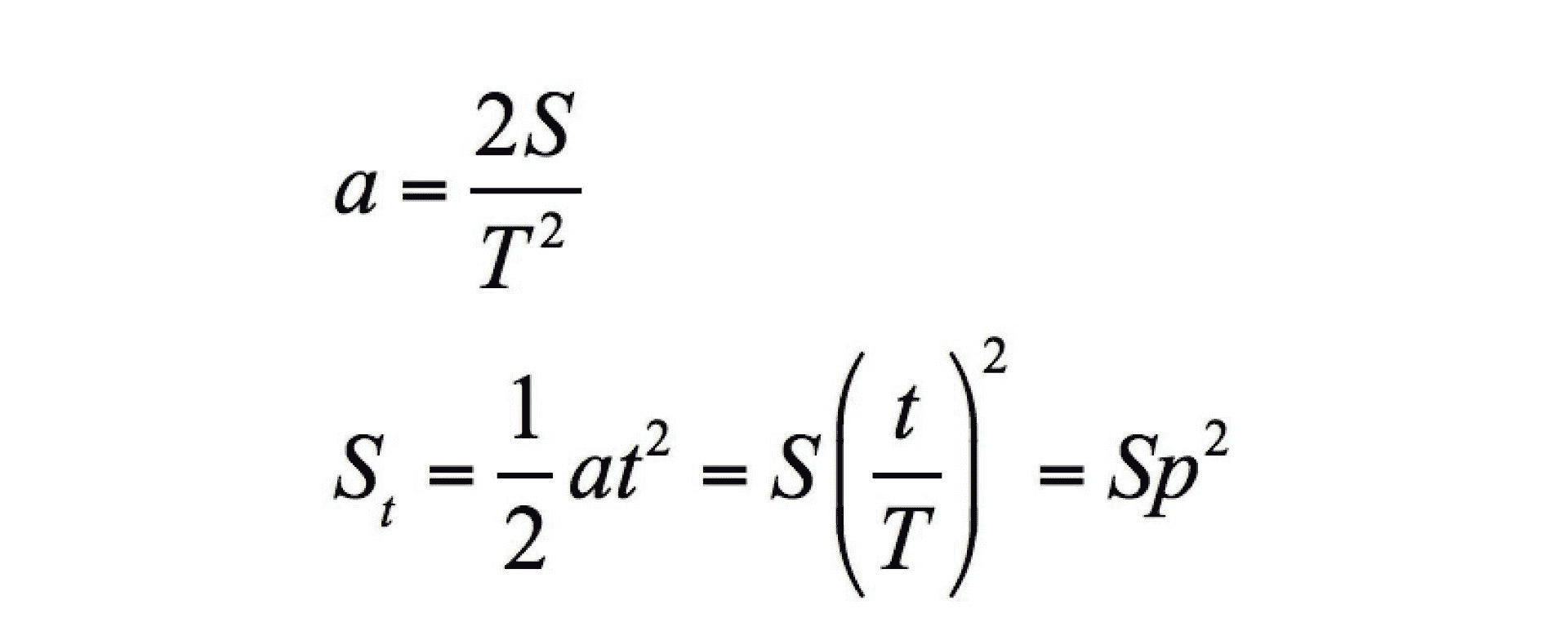
匀加速运动的计算公式
所以我们把 p 映射为 p 的平方。
还是同样的情况下,如果物体在做匀减速运动,那么,它在 t 时刻的位移和加速度的计算公式如下:

匀变速运动的计算公式
所以我们把 p 映射为 p(2-p)。
除此以外,我们还可以将 p 映射为三次曲线 p * p * (3.0 - 2.0 * p) ,来实现 smoothstep 的插值效果等等。那为了方便使用以及实现更多的效果,我们可以抽象出一个映射函数专门处理 p 的映射,这个函数叫做缓动函数(Easing Function)。
我们可以在前面实现过的 Timing 类中,直接增加一个缓动函数 easing。这样在获取 p 值的时候,我们直接用 this.easing(progress) 取代之前的 progress,就可以让动画变速运动了。修改后的代码如下:
export class Timing {
constructor({duration, iterations = 1, easing = p => p} = {}) {
this.startTime = Date.now();
this.duration = duration;
this.iterations = iterations;
this.easing = easing;
}
get time() {
return Date.now() - this.startTime;
}
get p() {
const progress = Math.min(this.time / this.duration, this.iterations);
return this.isFinished ? 1 : this.easing(progress % 1);
}
get isFinished() {
return this.time / this.duration >= this.iterations;
}
}
那带入到具体的例子中,我们只要多给 animator 传一个 easing 参数,就可以让一开始匀速运动的小方块变成匀加速运动了。下面就是我们使用这个缓动函数的具体代码:
import {Animator} from ‘../common/lib/animator/index.js’;
const block = document.querySelector(’.block’);
const animator = new Animator({duration: 3000, easing: p => p ** 2});
document.addEventListener(‘click’, () => {
animator.animate({el: block, start: 100, end: 400}, ({target: {el, start, end}, timing: {p}}) => {
const left = start * (1 - p) + end * p;
el.style.left = ${left}px;
});
});
贝塞尔曲线缓动
现在,我们已经缓动函数的应用了。缓动函数有很多种,其中比较常用的是贝塞尔曲线缓动(Bezier-easing),准确地说,是三次贝塞尔曲线缓动函数。接下来,我们就来一起来实现一个简单的贝塞尔曲线缓动。
我们先来复习一下三次贝塞尔曲线的参数方程:

对于贝塞尔曲线图形来说,t 是参数,P 是坐标。而贝塞尔曲线缓动函数,则是把 Px 作为时间参数 p,把 Py 作为 p 的映射。这样,我们就知道了参数方程和缓动函数之间映射关系了。
贝塞尔缓动函数,图盘来源:React.js
那要想把三次贝塞尔曲线参数方程变换成贝塞尔曲线缓动函数,我们可以使用一种数学方法,叫做牛顿迭代法(Newton’s method)。因为这个方法比较复杂,所以我就不展开细说了。
我们可以使用现成的 JavaScript 库bezier-easing来生成贝塞尔缓动函数,例如:
import {Animator} from ‘../common/lib/animator/index.js’;
const block = document.querySelector(’.block’);
const animator = new Animator({duration: 3000, easing: BezierEasing(0.5, -1.5, 0.5, 2.5)});
document.addEventListener(‘click’, () => {
animator.animate({el: block, start: 100, end: 400}, ({target: {el, start, end}, timing: {p}}) => {
const left = start * (1 - p) + end * p;
el.style.left = ${left}px;
});
});
这样,我们能得到如下的效果:

实际上,CSS3 动画原生支持 bezier-easing。所以上面的效果,我们也可以使用 CSS3 动画来实现。
.container {
display: flex;
flex-wrap: wrap;
justify-content: space-between;
width: 300px;
}
.block {
width: 100px;
height: 100px;
position: absolute;
top: 100px;
left: 100px;
background: blue;
flex-shrink: 0;
transform-origin: 50% 50%;
}
.animate {
animation: mymove 3s cubic-bezier(0.5, -1.5, 0.5, 2.5) forwards;
}
@keyframes mymove {
from {left: 100px}
to {left: 400px}
}
其实贝塞尔缓动函数还有很多种,你可以去easing.net这个网站里看一看,然后尝试利用里面提供的缓动函数,来修改我们例子代码中的效果,看看动画过程有什么不同。
要点总结
这节课,我们讲了动画的三种形式和实现它们的基本方法,并且我们重点讨论了由时序动画衍生的标准动画模型,以及在此基础上,利用线性插值和缓动函数来控制更多动画细节。
首先,我们来回顾一下这三种形式的实现方法和各自的特点:
- 第一种,固定帧动画。它实现起来最简单,只需要我们为每一帧准备一张图片,然后循环播放就可以了。
- 第二种,增量动画。虽然在实现的时候,我们需要在每帧给元素的相关属性增加一定的量,但也很好操作,就是不好精确控制动画细节。
- 第三种是使用时间和动画函数来描述的动画,也叫做时序动画。这种方法能够非常精确地控制动画的细节,所以它能实现的动画效果更丰富,应用最广泛。
然后,为了更方便使用,我们根据时序动画定义了标准动画模型,实现了 Animator 类。基于此,我们就可以使用线性插值来实现动画的匀速运动,通过缓动函数来改变动画的运动速度。
在动画的实现中,比较常用贝塞尔曲线缓动函数。它是通过对贝塞尔曲线方程进行牛顿迭代求出,我们可以使用 bezier-easing 库来创建贝塞尔缓动函数。CSS3 动画原生支持 bezier-easing,所以如果使用 HTML/CSS 方式绘制元素,我们可以尽量使用 CSS3 动画。
小试牛刀
最后,我希望你能利用我们今天学到的时序动画,来实现一个简单的动画效果。就是我们假设,有一个半径为 10px 的弹性小球,我们让它以自由落体的方式下落 200px 高度。在这个过程中,小球每次落地后弹起的高度会是之前的一半,然后它会不断重复自由下落的过程,直到静止在地面上。
你能试着用标准动画模型封装好的 Animator 模块,来实现这个效果吗?Animator 模块的代码你可以在 Github 仓库中找到,也可以直接按照我们前面讲解内容自己实现一下。
源码
本节课的完整示例代码见GitHub 仓库
推荐阅读
[1] 牛顿迭代法
[2] Bezier-easing
[3] Easing.net
文章作者 anonymous
上次更新 2024-02-10
