20|如何用WebGL绘制3D物体?
文章目录
你好,我是月影。这一节课开始,我们学习 3D 图形的绘制。
之前我们主要讨论的都是 2D 图形的绘制,实际上 WebGL 真正强大之处在于,它可以绘制各种 3D 图形,而 3D 图形能够极大地增强可视化的表现能力。
用 WebGL 绘制 3D 图形,其实在基本原理上和绘制 2D 图形并没有什么区别,只不过是我们把绘图空间从二维扩展到三维,所以计算起来会更加复杂一些。
今天,我们就从绘制最简单的三维立方体,讲到矩阵、法向量在三维空间中的使用,这样由浅入深地带你去了解,如何用 WebGL 绘制出各种 3D 图形。
如何用 WebGL 绘制三维立方体
首先,我们来绘制熟悉的 2D 图形,比如矩形,再把它拓展到三维空间变成立方体。代码如下:
// vertex shader 顶点着色器
attribute vec2 a_vertexPosition;
attribute vec4 color;
varying vec4 vColor;
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = vec4(a_vertexPosition, 1, 1);
}
// fragment shader 片元着色器
#ifdef GL_ES
precision highp float;
#endif
varying vec4 vColor;
void main() {
gl_FragColor = vColor;
}
…
// 顶点信息
renderer.setMeshData([{
positions: [
[-0.5, -0.5],
[-0.5, 0.5],
[0.5, 0.5],
[0.5, -0.5],
],
attributes: {
color: [
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 0, 0, 1],
],
},
cells: [[0, 1, 2], [0, 2, 3]],
}]);
renderer.render();
上面的 3 段代码,分别对应顶点着色器、片元着色器和基本的顶点信息。通过它们,我们就在画布上绘制出了一个红色的矩形。接下来,要想把 2 维矩形拓展到 3 维,我们的第一步就是要把顶点扩展到 3 维。这一步的操作比较简单,我们只需要把顶点从 vec2 扩展到 vec3 就可以了。
// vertex shader
attribute vec3 a_vertexPosition;
attribute vec4 color;
varying vec4 vColor;
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = vec4(a_vertexPosition, 1);
}
然后,我们需要计算立方体的顶点数据。我们知道一个立方体有 8 个顶点,这 8 个顶点能组成 6 个面。在 WebGL 中,我们就需要用 12 个三角形来绘制它。如果每个面的属性相同,我们就可以复用 8 个顶点来绘制。而如果属性不同,比如每个面要绘制成不同的颜色,或者添加不同的纹理图片,我们还得把每个面的顶点分开。这样的话,我们一共需要 24 个顶点。

立方体 8 个顶点,6 个面
为了方便使用,我们可以写一个 JavaScript 函数,用来生成立方体 6 个面的 24 个顶点,以及 12 个三角形的索引,而且我直接在这个函数里定义了每个面的颜色。具体的函数代码如下:
function cube(size = 1.0, colors = [[1, 0, 0, 1]]) {
const h = 0.5 * size;
const vertices = [
[-h, -h, -h],
[-h, h, -h],
[h, h, -h],
[h, -h, -h],
[-h, -h, h],
[-h, h, h],
[h, h, h],
[h, -h, h],
];
const positions = [];
const color = [];
const cells = [];
let colorIdx = 0;
let cellsIdx = 0;
const colorLen = colors.length;
function quad(a, b, c, d) {
[a, b, c, d].forEach((i) => {
positions.push(vertices[i]);
color.push(colors[colorIdx % colorLen]);
});
cells.push(
[0, 1, 2].map(i => i + cellsIdx),
[0, 2, 3].map(i => i + cellsIdx),
);
colorIdx++;
cellsIdx += 4;
}
quad(1, 0, 3, 2);
quad(4, 5, 6, 7);
quad(2, 3, 7, 6);
quad(5, 4, 0, 1);
quad(3, 0, 4, 7);
quad(6, 5, 1, 2);
return {positions, color, cells};
}
这样,我们就可以构建出立方体的顶点信息,我在下面给出了 12 个立方体的顶点。
const geometry = cube(1.0, [
[1, 0, 0, 1],
[0, 0.5, 0, 1],
[1, 0, 1, 1],
]);
通过上面的代码,我们就能创建出一个棱长为 1 的立方体,并且六个面的颜色分别是“红、绿、蓝、红、绿、蓝”。
这里我还想补充一点内容,绘制 3D 图形与绘制 2D 图形有一点不一样,那就是我们必须要开启深度检测和启用深度缓冲区。在 WebGL 中,我们可以通过gl.enable(gl.DEPTH_TEST),来开启深度检测。
而且,我们在清空画布的时候,也要用gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);,来同时清空颜色缓冲区和深度缓冲区。启动和清空深度检测和深度缓冲区这两个步骤,是这个过程中非常重要的一环,但是我们几乎不会用原生的方式来写代码,所以我们了解到这个程度就可以了。
事实上,对于上面这些步骤,为了方便使用,我们还是可以直接使用 gl-renderer 库。它封装了深度检测,在使用它的时候,我们只要在创建 renderer 的时候设置一个参数 depth: true 即可。
现在,我们把这个三维立方体用 gl-renderer 渲染出来,渲染代码如下:
const canvas = document.querySelector(‘canvas’);
const renderer = new GlRenderer(canvas, {
depth: true,
});
const program = renderer.compileSync(fragment, vertex);
renderer.useProgram(program);
renderer.setMeshData([{
positions: geometry.positions,
attributes: {
color: geometry.color,
},
cells: geometry.cells,
}]);
renderer.render();

立方体的正视图,在画布上只呈现了一个红色正方形,因为其他面被遮挡住了
投影矩阵:变换 WebGL 坐标系
结合渲染出来的这个图形,我想让你再仔细观看一下我们刚才调用的代码。
当时立方体的顶点我们是这么定义的:
const vertices = [
[-h, -h, -h],
[-h, h, -h],
[h, h, -h],
[h, -h, -h],
[-h, -h, h],
[-h, h, h],
[h, h, h],
[h, -h, h],
而立方体的六个面的颜色,我们是这么定义的:
//立方体的六个面
quad(1, 0, 3, 2); // 红 – 这一面应该朝内
quad(4, 5, 6, 7); // 绿 – 这一面应该朝外
quad(2, 3, 7, 6); // 蓝
quad(5, 4, 0, 1); // 红
quad(3, 0, 4, 7); // 绿
quad(6, 5, 1, 2); // 蓝
有没有发现问题?我们之前说过,WebGL 的坐标系是 z 轴向外为正,z 轴向内为负,所以根据我们调用的代码,赋给靠外那一面的颜色应该是绿色,而不是红色。但是这个立方体朝向我们的一面却是红色,这是为什么呢?
实际上,WebGL 默认的剪裁坐标的 z 轴方向,的确是朝内的。也就是说,WebGL 坐标系就是一个左手系而不是右手系。但是,基本上所有的 WebGL 教程,也包括我们前面的课程,一直都在说 WebGL 坐标系是右手系,这又是为什么呢?
这是因为,规范的直角坐标系是右手坐标系,符合我们的使用习惯。因此,一般来说,不管什么图形库或图形框架,在绘图的时候,都会默认将坐标系从左手系转换为右手系。
**那我们下一步,就是要将 WebGL 的坐标系从左手系转换为右手系。**关于坐标转换,我们可以通过齐次矩阵来完成。将左手系坐标转换为右手系,实际上就是将 z 轴坐标方向反转,对应的齐次矩阵如下:
[
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, -1, 0,
0, 0, 0, 1
]
这种转换坐标的齐次矩阵,又被称为投影矩阵(ProjectionMatrix)。接着,我们就修改一下顶点着色器,将投影矩阵加入进去。这样,画布上显示的就是绿色的正方形了。代码和效果图如下:
attribute vec3 a_vertexPosition;
attribute vec4 color;
varying vec4 vColor;
uniform mat4 projectionMatrix;
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = projectionMatrix * vec4(a_vertexPosition, 1.0);
}

投影矩阵不仅可以用来改变 z 轴坐标,还可以用来实现正交投影、透视投影以及其他的投影变换,在下一节课我们会深入去讲。
模型矩阵:让立方体旋转起来
通过前面的操作,我们还是只能看到立方体的一个面,因为我们的视线正好是垂直于 z 轴的,所以其他的面被完全挡住了。不过,我们可以通过旋转立方体,将其他的面露出来。旋转立方体,同样可以通过矩阵运算来实现。这次我们要用到另一个齐次矩阵,它定义了被绘制的物体变换,这个矩阵叫做模型矩阵(ModelMatrix)。接下来,我们就把模型矩阵加入到顶点着色器中,然后将它与投影矩阵相乘,最后再乘上齐次坐标,就得到最终的顶点坐标了。
attribute vec3 a_vertexPosition;
attribute vec4 color;
varying vec4 vColor;
uniform mat4 projectionMatrix;
uniform mat4 modelMatrix;
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = projectionMatrix * modelMatrix * vec4(a_vertexPosition, 1.0);
}
接着,我们定义一个 JavaScript 函数,用立方体沿 x、y、z 轴的旋转来生成模型矩阵。我们以 x、y、z 三个方向的旋转得到三个齐次矩阵,然后将它们相乘,就能得到最终的模型矩阵。
import {multiply} from ‘../common/lib/math/functions/Mat4Func.js’;
function fromRotation(rotationX, rotationY, rotationZ) {
let c = Math.cos(rotationX);
let s = Math.sin(rotationX);
const rx = [
1, 0, 0, 0,
0, c, s, 0,
0, -s, c, 0,
0, 0, 0, 1,
];
c = Math.cos(rotationY);
s = Math.sin(rotationY);
const ry = [
c, 0, s, 0,
0, 1, 0, 0,
-s, 0, c, 0,
0, 0, 0, 1,
];
c = Math.cos(rotationZ);
s = Math.sin(rotationZ);
const rz = [
c, s, 0, 0,
-s, c, 0, 0,
0, 0, 1, 0,
0, 0, 0, 1,
];
const ret = [];
multiply(ret, rx, ry);
multiply(ret, ret, rz);
return ret;
}
最后,我们把这个模型矩阵传给顶点着色器,不断更新三个旋转角度,就能实现立方体旋转的效果,也就可以看到立方体其他各个面了。效果和代码如下所示:
let rotationX = 0;
let rotationY = 0;
let rotationZ = 0;
function update() {
rotationX += 0.003;
rotationY += 0.005;
rotationZ += 0.007;
renderer.uniforms.modelMatrix = fromRotation(rotationX, rotationY, rotationZ);
requestAnimationFrame(update);
}
update();

到这里,我们就完成了一个旋转的立方体。
如何用 WebGL 绘制圆柱体
立方体还是比较简单的几何体,那类似的,我们还可以构建顶点和三角形,来绘制更加复杂的图形,比如圆柱体、球体等等。这里,我再用绘制圆柱体来举个例子。
我们知道圆柱体的两个底面都是圆,我们可以用割圆的方式对圆进行简单的三角剖分,然后把圆柱的侧面用上下两个圆上的顶点进行三角剖分。

具体的算法如下:
function cylinder(radius = 1.0, height = 1.0, segments = 30, colorCap = [0, 0, 1, 1], colorSide = [1, 0, 0, 1]) {
const positions = [];
const cells = [];
const color = [];
const cap = [[0, 0]];
const h = 0.5 * height;
// 顶和底的圆
for(let i = 0; i <= segments; i++) {
const theta = Math.PI * 2 * i / segments;
const p = [radius * Math.cos(theta), radius * Math.sin(theta)];
cap.push(p);
}
positions.push(…cap.map(([x, y]) => [x, y, -h]));
for(let i = 1; i < cap.length - 1; i++) {
cells.push([0, i, i + 1]);
}
cells.push([0, cap.length - 1, 1]);
let offset = positions.length;
positions.push(…cap.map(([x, y]) => [x, y, h]));
for(let i = 1; i < cap.length - 1; i++) {
cells.push([offset, offset + i, offset + i + 1]);
}
cells.push([offset, offset + cap.length - 1, offset + 1]);
color.push(…positions.map(() => colorCap));
// 侧面
offset = positions.length;
for(let i = 1; i < cap.length; i++) {
const a = […cap[i], h];
const b = […cap[i], -h];
const nextIdx = i < cap.length - 1 ? i + 1 : 1;
const c = […cap[nextIdx], -h];
const d = […cap[nextIdx], h];
positions.push(a, b, c, d);
color.push(colorSide, colorSide, colorSide, colorSide);
cells.push([offset, offset + 1, offset + 2], [offset, offset + 2, offset + 3]);
offset += 4;
}
return {positions, cells, color};
}
这样呢,我们就可以绘制出圆柱体了,把前面例子代码里的 cube 改为 cylinder,效果如下图所示:

所以我们看到,用 WebGL 绘制三维物体,实际上和绘制二维物体没有什么本质不同,都是将图形(对于三维来说,也就是几何体)的顶点数据构造出来,然后将它们送到缓冲区中,再执行绘制。只不过三维图形的绘制需要构造三维的顶点和网格,在绘制前还需要启用深度缓冲区。
构造和使用法向量
在前面两个例子中,我们构造出了几何体的顶点信息,包括顶点的位置和颜色信息,除此之外,我们还可以构造几何体的其他信息,其中一种比较有用的信息是顶点的法向量信息。
法向量那什么是法向量呢?法向量表示每个顶点所在的面的法线方向,在 3D 渲染中,我们可以通过法向量来计算光照、阴影、进行边缘检测等等。法向量非常有用,所以我们也要掌握它的构造方法。
1. 构造法向量
对于立方体来说,得到法向量非常简单,我们只要找到垂直于立方体 6 个面上的线段,再得到这些线段所在向量上的单位向量就行了。显然,标准立方体中 6 个面的法向量如下:
[0, 0, -1]
[0, 0, 1]
[0, -1, 0]
[0, 1, 0]
[-1, 0, 0]
[1, 0, 0]
对于圆柱体来说,底面和顶面法线分别是 (0, 0, -1) 和 (0, 0, 1)。侧面的计算稍微复杂一些,需要通过三角网格来计算。具体怎么做呢?
因为几何体是由三角网格构成的,而法线是垂直于三角网格的线,如果要计算法线,我们可以借助三角形的顶点,使用向量的叉积定理来求。我们假设在一个平面内,有向量 a 和 b,n 是它们的法向量,那我们可以得到公式:n = a X b。
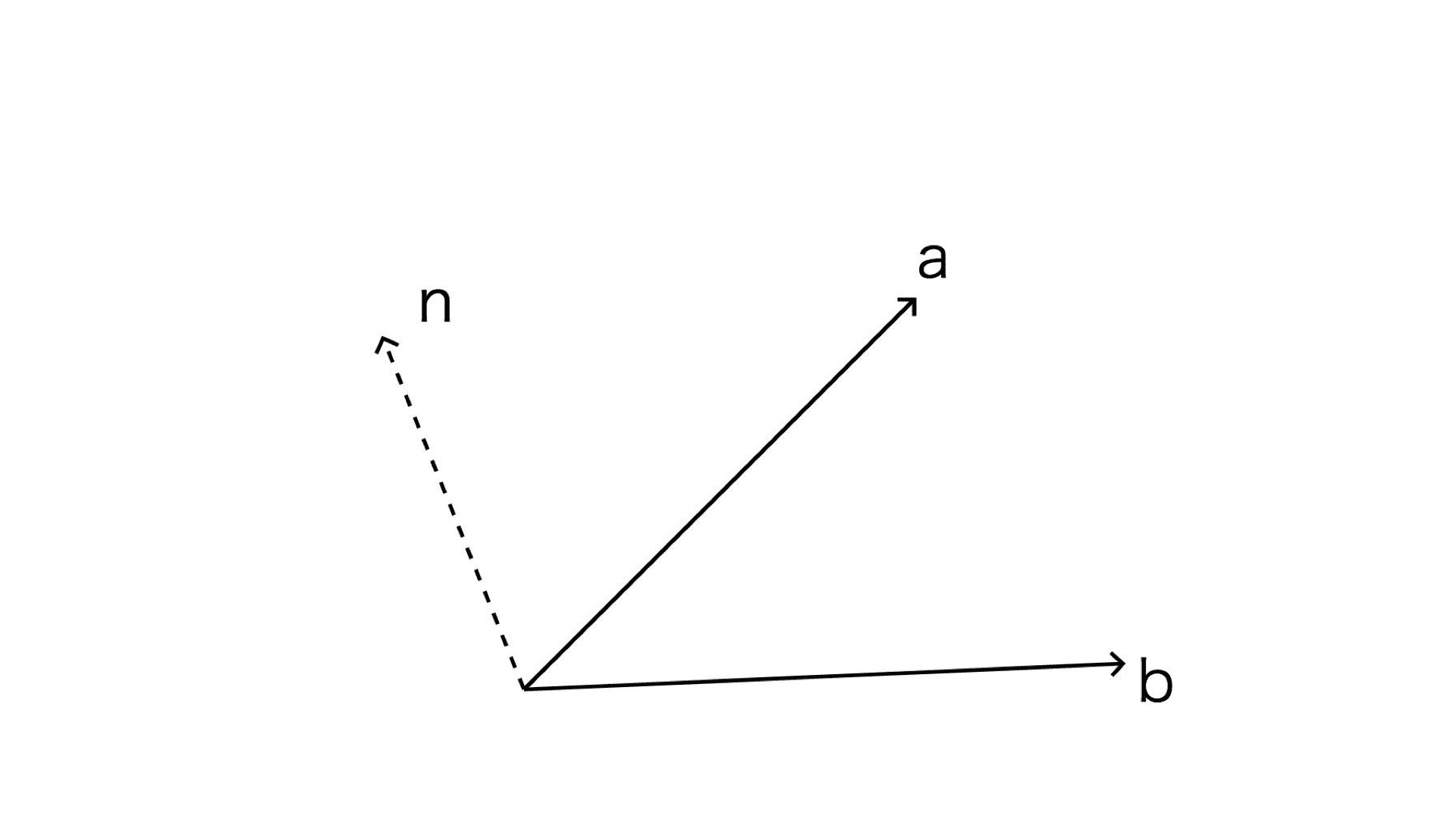
根据这个公式,我们可以通过以下方法求出侧面的法向量:
const tmp1 = [];
const tmp2 = [];
// 侧面
offset = positions.length;
for(let i = 1; i < cap.length; i++) {
const a = […cap[i], h];
const b = […cap[i], -h];
const nextIdx = i < cap.length - 1 ? i + 1 : 1;
const c = […cap[nextIdx], -h];
const d = […cap[nextIdx], h];
positions.push(a, b, c, d);
const norm = [];
cross(norm, subtract(tmp1, b, a), subtract(tmp2, c, a));
normalize(norm, norm);
normal.push(norm, norm, norm, norm); // abcd 四个点共面,它们的法向量相同
color.push(colorSide, colorSide, colorSide, colorSide);
cells.push([offset, offset + 1, offset + 2], [offset, offset + 2, offset + 3]);
offset += 4;
}
求出法向量,我们可以使用法向量来实现丰富的效果,比如点光源。下面,我们就在 shader 中实现点光源效果。
2. 法向量矩阵
因为我们在 shader 中,会使用模型矩阵对顶点进行变换,所以在片元着色器中,我们拿到的是变换后的顶点坐标,这时候,如果我们要应用法向量,需要对法向量也进行变换,我们可以通过一个矩阵来实现,这个矩阵叫做法向量矩阵(NormalMatrix)。它是模型矩阵的逆转置矩阵,不过它非常特殊,是一个 3X3 的矩阵(mat3),而像模型矩阵、投影矩阵等等矩阵都是 4X4 的。
得到了法向量和法向量矩阵,我们可以使用法向量和法向量矩阵来实现点光源光照效果。首先,我们要实现如下顶点着色器:
attribute vec3 a_vertexPosition;
attribute vec4 color;
attribute vec3 normal;
varying vec4 vColor;
varying float vCos;
uniform mat4 projectionMatrix;
uniform mat4 modelMatrix;
uniform mat3 normalMatrix;
const vec3 lightPosition = vec3(1, 0, 0);
void main() {
gl_PointSize = 1.0;
vColor = color;
vec4 pos = modelMatrix * vec4(a_vertexPosition, 1.0);
vec3 invLight = lightPosition - pos.xyz;
vec3 norm = normalize(normalMatrix * normal);
vCos = max(dot(normalize(invLight), norm), 0.0);
gl_Position = projectionMatrix * pos;
}
在上面顶点着色器的代码中,我们计算的是位于 (1,0,0) 坐标处的点光源与几何体法线的夹角余弦。那根据物体漫反射模型,光照强度等于光线与法向量夹角的余弦。

因此,我们求出这个余弦值,就能在片元着色器叠加光照了。操作代码和实现效果如下:
#ifdef GL_ES
precision highp float;
#endif
uniform vec4 lightColor;
varying vec4 vColor;
varying float vCos;
void main() {
gl_FragColor.rgb = vColor.rgb + vCos * lightColor.a * lightColor.rgb;
gl_FragColor.a = vColor.a;
}

用法向量计算出的光照效果
要点总结
今天,我们以绘制立方体和圆柱体为例,讲了用 WebGL 绘制三维几何体的基本原理。3D 绘图在原理上和 2D 绘图几乎是完全一样的,就是构建顶点数据,然后将数据送入缓冲区执行绘制。只是,2D 绘图用二维顶点数据,而 3D 绘图用三维定点数据。
另外,3D 绘图时,我们除了构造顶点数据之外,还可以构造其他的数据,比较有用的是法向量。法向量是垂直于物体表面三角网格的向量,使用它可以来计算光照。在片元着色器中我们拿到的是经过模型矩阵变换后的顶点,使用法向量,我们还需要用一个法向量矩阵对它进行变换。法向量矩阵是模型矩阵的逆转置矩阵,它是一个 3X3 的矩阵,将法向量经过法向量矩阵变换后,我们就可以和片元着色器中的顶点进行运算了。
小试牛刀
- 在今天的课程中,我们绘制出了正立方体。那你能修改例子中的 cube 函数,构造出非正立方体吗?新的 cube 函数签名如下:
function cube(width = 1.0, height = 1.0, depth = 1.0, colors = [[1, 0, 0, 1]])
- 你能用我们今天讲的方法绘制出一个正四面体,并给不同的面设置不同的颜色,然后在正四面体上实现点光源光照效果吗?
欢迎在留言区和我讨论,分享你的答案和思考,也欢迎你把这节课分享给你的朋友,我们下节课见!
源码
课程中完整示例代码见 GitHub 仓库
文章作者 anonymous
上次更新 2024-02-10