21|如何添加相机,用透视原理对物体进行投影?
文章目录
你好,我是月影。
上节课,我们在绘制 3D 几何体的时候,实际上有一个假设,那就是观察者始终从三维空间坐标系的正面,也就是 z 轴正方向,看向坐标原点。但在真实世界的模型里,观察者可以处在任何一个位置上。
那今天,我们就在上节课的基础上,引入一个空间观察者的角色,或者说是相机(Camera),来总结一个更通用的绘图模型。这样,我们就能绘制出,从三维空间中任意一个位置观察物体的效果了。
首先,我们来说说什么是相机。
如何理解相机和视图矩阵?
我们现在假设,在 WebGL 的三维世界任意位置上有一个相机,它可以用一个三维坐标(Position)和一个三维向量方向(LookAt Target)来表示。
在初始情况下,相机的参考坐标和世界坐标是重合的。但是,当我们移动或者旋转相机的时候,相机的参考坐标和世界坐标就不重合了。
而我们最终要在 Canvas 画布上绘制出的是,以相机为观察者的图形,所以我们就需要用一个变换,将世界坐标转换为相机坐标。这个变换的矩阵就是视图矩阵(ViewMatrix)。
计算视图矩阵比较简单的一种方法是,我们先计算相机的模型矩阵,然后对矩阵使用 lookAt 函数,这样我们得到的矩阵就是视图矩阵的逆矩阵。然后,我们再对这个逆矩阵求一次逆,就可以得到视图矩阵了。
这么说还是有点比较抽象,我们通过代码来理解。
function updateCamera(eye, target = [0, 0, 0]) {
const [x, y, z] = eye;
const m = new Mat4(
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0,
x, y, z, 1,
);
const up = [0, 1, 0];
m.lookAt(eye, target, up).inverse();
renderer.uniforms.viewMatrix = m;
}
如上面代码所示,我们设置相机初始位置矩阵 m,然后执行 m.lookAt(eye, target, up),这里的 up 是一个向量,表示朝上的方向,我们把它定义为 y 轴正向。然后我们调用 inverse,将这个结果求逆,得到的就是视图矩阵。
为了让你看到相机的效果,我们改写上节课圆柱体的顶点着色器代码,加入视图矩阵。
attribute vec3 a_vertexPosition;
attribute vec4 color;
attribute vec3 normal;
varying vec4 vColor;
varying float vCos;
uniform mat4 projectionMatrix;
uniform mat4 modelMatrix;
uniform mat4 viewMatrix;
uniform mat3 normalMatrix;
const vec3 lightPosition = vec3(1, 0, 0);
void main() {
gl_PointSize = 1.0;
vColor = color;
vec4 pos = viewMatrix * modelMatrix * vec4(a_vertexPosition, 1.0);
vec4 lp = viewMatrix * vec4(lightPosition, 1.0);
vec3 invLight = lp.xyz - pos.xyz;
vec3 norm = normalize(normalMatrix * normal);
vCos = max(dot(normalize(invLight), norm), 0.0);
gl_Position = projectionMatrix * pos;
}
这样,如果我们就把相机位置改变了。我们以 updateCamera([0.5, 0, 0.5]); 为例,这样朝向 (0, 0, 0) 拍摄图像的最终效果就如下所示。

剪裁空间和投影对 3D 图像的影响
在前面的课程中我们说过,WebGL 的默认坐标范围是从 -1 到 1 的。也就是说,只有当图像的 x、y、z 的值在 -1 到 1 区间内才会被显示在画布上,而在其他位置上的图像都会被剪裁掉。
举个例子,如果我们修改模型矩阵,让圆柱体沿 x、y 轴平移,向右上方各平移 0.5,那么圆柱中 x、y 值大于 1 的部分都会被剪裁掉,因为这些部分已经超过了 Canvas 边缘。操作代码和最终效果如下:
function update() {
const modelMatrix = fromRotation(rotationX, rotationY, rotationZ);
modelMatrix[12] = 0.5; // 给 x 轴增加 0.5 的平移
modelMatrix[13] = 0.5; // 给 y 轴也增加 0.5 的平移
renderer.uniforms.modelMatrix = modelMatrix;
renderer.uniforms.normalMatrix = normalFromMat4([], modelMatrix);
…
}

给 x、y 增加 0.5 平移后的效果
对于只有 x、y 的二维坐标系来说,这一点很好理解。但是,对于三维坐标系来说,不仅 x、y 轴会被剪裁,z 轴同样也会被剪裁。我们还是直接修改代码,给 z 轴增加 0.5 的平移。你会看到,最终绘制出来的图形非常奇怪。

给 z 轴增加 0.5 平移后的效果
会显示这么奇怪的结果,就是因为 z 轴超过范围的部分也被剪裁掉了,导致投影出现了问题。
既然是投影出现了问题,我们先回想一下,我们都对 z 轴做过哪些投影操作。在绘制圆柱体的时候,我们只是用投影矩阵非常简单地反转了一下 z 轴,除此之外,没做过其他任何操作了。所以,为了让图形在剪裁空间中正确显示,我们不能只反转 z 轴,还需要将图像从三维空间中投影到剪裁坐标内。那么问题来了,图像是怎么被投影到剪裁坐标内的呢?
一般来说,投影有两种方式,分别是正投影与透视投影。你可以结合我给出的示意图,来理解它们各自的特点。
首先是正投影,它又叫做平行投影。正投影是将物体投影到一个长方体的空间(又称为视景体),并且无论相机与物体距离多远,投影的大小都不变。
正投影示意图
而透视投影则更接近我们的视觉感知。它投影的规律是,离相机近的物体大,离相机远的物体小。与正投影不同,正投影的视景体是一个长方体,而透视投影的视景体是一个棱台。
透视投影示意图
知道了不同投影方式的特点,我们就可以根据投影方式和给定的参数来计算投影矩阵了。因为数学推导过程比较复杂,我在这里就不详细推导了,直接给出对应的 JavaScript 函数,你只要记住 ortho 和 perspective 这两个投影函数就可以了,函数如下所示。
其中,ortho 是计算正投影的函数,它的参数是视景体 x、y、z 三个方向的坐标范围,它的返回值就是投影矩阵。而 perspective 是计算透视投影的函数,它的参数是近景平面 near、远景平面 far、视角 fov 和宽高比率 aspect,返回值也是投影矩阵。
// 计算正投影矩阵
function ortho(out, left, right, bottom, top, near, far) {
let lr = 1 / (left - right);
let bt = 1 / (bottom - top);
let nf = 1 / (near - far);
out[0] = -2 * lr;
out[1] = 0;
out[2] = 0;
out[3] = 0;
out[4] = 0;
out[5] = -2 * bt;
out[6] = 0;
out[7] = 0;
out[8] = 0;
out[9] = 0;
out[10] = 2 * nf;
out[11] = 0;
out[12] = (left + right) * lr;
out[13] = (top + bottom) * bt;
out[14] = (far + near) * nf;
out[15] = 1;
return out;
}
// 计算透视投影矩阵
function perspective(out, fovy, aspect, near, far) {
let f = 1.0 / Math.tan(fovy / 2);
let nf = 1 / (near - far);
out[0] = f / aspect;
out[1] = 0;
out[2] = 0;
out[3] = 0;
out[4] = 0;
out[5] = f;
out[6] = 0;
out[7] = 0;
out[8] = 0;
out[9] = 0;
out[10] = (far + near) * nf;
out[11] = -1;
out[12] = 0;
out[13] = 0;
out[14] = 2 * far * near * nf;
out[15] = 0;
return out;
}
接下来,我们先试试对圆柱体进行正投影。假设,在正投影的时候,我们让视景体三个方向的范围都是 (-2,2)。以刚才的相机位置为参照(任何一个位置观察都一样,不管物体在哪里,都是只有之前大小的一半。因为视景体范围增加了),我们绘制出来的圆柱体的大小只有之前的一半。这是因为我们通过投影变换将空间坐标范围增大了一倍。
import {ortho} from ‘../common/lib/math/functions/Mat4Func.js’;
function projection(left, right, bottom, top, near, far) {
return ortho([], left, right, bottom, top, near, far);
}
const projectionMatrix = projection(-2, 2, -2, 2, -2, 2);
renderer.uniforms.projectionMatrix = projectionMatrix; // 投影矩阵
updateCamera([0.5, 0, 0.5]); // 设置相机位置

接下来,我们再试一下对圆柱体进行透视投影。在进行透视投影的时候,我们将相机的位置放在 (2, 2, 3) 的地方。
import {perspective} from ‘../common/lib/math/functions/Mat4Func.js’;
function projection(near = 0.1, far = 100, fov = 45, aspect = 1) {
return perspective([], fov * Math.PI / 180, aspect, near, far);
}
const projectionMatrix = projection();
renderer.uniforms.projectionMatrix = projectionMatrix;
updateCamera([2, 2, 3]); // 设置相机位置

我们发现,在透视投影下,距离观察者(相机)近的部分大,距离它远的部分小。这更符合真实世界中我们看到的效果,所以一般来说,在绘制 3D 图形时,我们更偏向使用透视投影。
3D 绘图标准模型
实际上,通过上节课和刚才的内容,我们已经能总结出 3D 绘制几何体的基本数学模型,也就是 3D 绘图的标准模型。这个标准模型一共有四个矩阵,它们分别是:投影矩阵、视图矩阵(ViewMatrix)、模型矩阵(ModelMatrix)、法向量矩阵(NormalMatrix)。
其中,前三个矩阵用来计算最终显示的几何体的顶点位置,第四个矩阵用来实现光照等效果。比较成熟的图形库,如ThreeJS、BabylonJS,基本上都是采用这个标准模型来进行 3D 绘图的。所以理解这个模型,也有助于增强我们对图形库的认识,帮助我们更好地去使用这些流行的图形库。
在前面的课程中,因为 WebGL 原生的 API 在使用上比较复杂,所以我们使用了简易的 gl-renderer 库来简化 2D 绘图过程。而 3D 绘图是一个比 2D 绘图更加复杂的过程,即使是 gl-renderer 库也有点力不从心,我们需要更加强大的绘图库,来简化我们的绘制,以便于我们能够把精力专注于理解图形学本身的核心内容。
当然,使用 ThreeJS 或 BabeylonJS 都是不错的选择。但是在这节课中,我会使用一个更加轻量级的图形库,叫做OGL。它拥有我们可视化绘图需要的所有基本功能,而且,相比于 ThreeJS 等流行图形库,它的 AP 相对更底层、更简单一些。因此不会有太多高级的特性对我们的学习造成干扰。
接下来,我就用这个库来绘制一些简单的圆柱体、立方体等等,让你对这个库的使用有一个全面的了解。
如何使用 OGL 绘制基本的几何体
OGL 库使用的也是我们刚才说的标准模型,因此,使用它所以绘制几何体非常简单,分成以下 7 个步骤,如下图所示。
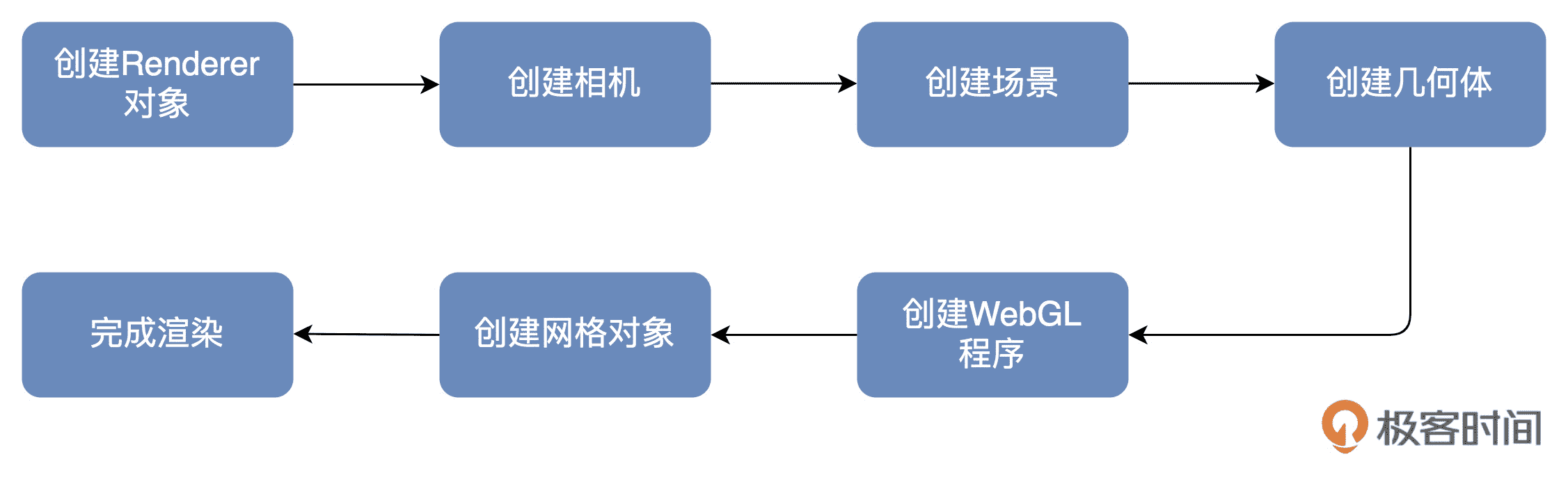
接下来,我们详细来看看每一步的操作。
首先,是创建 Renderer 对象。我们可以创建一个画布宽高为 512 的 Renderer 对象。代码如下:
const canvas = document.querySelector(‘canvas’);
const renderer = new Renderer({
canvas,
width: 512,
height: 512,
});
然后,我们在 OGL 中,通过 new Camera 来创建相机,默认创建出的是透视投影相机。这里我们把视角设置为 35 度,位置设置为 (0,1,7),朝向为 (0,0,0)。代码如下:
const gl = renderer.gl;
gl.clearColor(1, 1, 1, 1);
const camera = new Camera(gl, {fov: 35});
camera.position.set(0, 1, 7);
camera.lookAt([0, 0, 0]);
接着,我们创建场景。OGL 使用树形渲染的方式,所以在用 OGL 创建场景时,我们要使用 Transform 元素。Transform 类型是基本元素,它可以添加子元素和设置几何变换,如果父元素设置了变换,这些变换也会被应用到子元素。
const scene = new Transform();
然后,我们创建几何体对象。OGL 内置了许多常用的几何体对象,包括球体 Sphere、立方体 Box、柱 / 锥体 Cylinder 以及环面 Torus 等等。使用这些对象,我们可以快速创建这些几何体的顶点信息。那在这里,我创建了 4 个几何体对象,分别是球体、立方体、椎体和环面。
const sphereGeometry = new Sphere(gl);
const cubeGeometry = new Box(gl);
const cylinderGeometry = new Cylinder(gl);
const torusGeometry = new Torus(gl);
再然后,我们创建 WebGL 程序。并且,我们在着色器中给这些几何体设置了浅蓝色和简单的光照效果。
const vertex = /* glsl */ `
precision highp float;
attribute vec3 position;
attribute vec3 normal;
uniform mat4 modelViewMatrix;
uniform mat4 projectionMatrix;
uniform mat3 normalMatrix;
varying vec3 vNormal;
void main() {
vNormal = normalize(normalMatrix * normal);
gl_Position = projectionMatrix * modelViewMatrix * vec4(position, 1.0);
}
`;
const fragment = /* glsl */ `
precision highp float;
varying vec3 vNormal;
void main() {
vec3 normal = normalize(vNormal);
float lighting = dot(normal, normalize(vec3(-0.3, 0.8, 0.6)));
gl_FragColor.rgb = vec3(0.2, 0.8, 1.0) + lighting * 0.1;
gl_FragColor.a = 1.0;
}
`;
const program = new Program(gl, {
vertex,
fragment,
});
有了 WebGL 程序之后,我们使用它和几何体对象来构建真正的网格(Mesh)元素,最终再把这些元素渲染到画布上。我们创建了 4 个网格对象,它们的形状分别是环面、球体、立方体和圆柱,我们给它们设置了不同的位置,然后将它们添加到场景 scene 中去。
const torus = new Mesh(gl, {geometry: torusGeometry, program});
torus.position.set(0, 1.3, 0);
torus.setParent(scene);
const sphere = new Mesh(gl, {geometry: sphereGeometry, program});
sphere.position.set(1.3, 0, 0);
sphere.setParent(scene);
const cube = new Mesh(gl, {geometry: cubeGeometry, program});
cube.position.set(0, -1.3, 0);
cube.setParent(scene);
const cylinder = new Mesh(gl, {geometry: cylinderGeometry, program});
cylinder.position.set(-1.3, 0, 0);
cylinder.setParent(scene);
最后,我们将它们用相机 camera 对象的设定渲染出来,并分别设置绕 y 轴旋转的动画,你就能看到这 4 个图像旋转的画面了。代码如下:
requestAnimationFrame(update);
function update() {
requestAnimationFrame(update);
torus.rotation.y -= 0.02;
sphere.rotation.y -= 0.03;
cube.rotation.y -= 0.04;
cylinder.rotation.y -= 0.02;
renderer.render({scene, camera});
}

要点总结
在这一节课,我们在三维空间里,引入了相机和视图矩阵的概念,相机分为透视相机和正交相机,它们有不同的投影方式,并且设置它们还可以改变剪裁空间。视图矩阵和前一节课介绍的投影矩阵、模型矩阵、法向量矩阵一起,构成了 3D 绘图标准模型,这是一般的图形库遵循的标准绘图方式。
为了巩固学习到的知识,我们使用 OGL 库来尝试绘制不同的 3D 几何体,我们依次用 OGL 绘制了球体、立方体、圆柱体和环面。OGL 绘制图形的基本步骤可以总结为 7 步,如下图:

小试牛刀
- 在上面的例子里,使用 OGL 绘制的球体看起来不是很圆,你可以研究一下OGL 的代码,修改一下创建球体的参数,让它看起来更圆。
- 你能试着修改一下片元着色器,让上面绘制的 4 个几何体呈现不同的颜色吗?将它们分别改成红色、黄色、蓝色和绿色。
欢迎在留言区和我讨论,分享你的答案和思考,也欢迎你把这节课分享给你的朋友,我们下节课见!
源码
课程中完整示例代码详见GitHub 仓库
推荐阅读
OGL
文章作者 anonymous
上次更新 2024-02-10

