03|矩阵:为什么说矩阵是线性方程组的另一种表达?
文章目录
你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我们要讲的内容是“矩阵”。
在开始学习之前,我想先问你个问题,你觉得,学习矩阵有什么用呢?你可以先自己想一想。之后我们讲任何一个知识的时候,你都可以从这个角度出发,自己先思考一下,这样有助于你对所学内容理解得更深刻。
对于刚才那个问题,我的答案很简单,就一句话,从我们程序员的角度去理解的话,矩阵可以极大地提高计算机的运算效率。怎么说呢?我给你举一个例子。在机器学习中(特别是深度学习,或者更具体一点,神经网络),并行计算是非常昂贵的。

上图是一个典型的神经网络架构,在这时候,矩阵就能发挥用武之地了,计算 H 隐藏层输出的公式是:H=f(W.x+b),其中 W 是权重矩阵,f 是激活函数,b 是偏差,x 是输入层矩阵。而这个计算过程就叫做向量化(Vectorization),这也是 GPU 在深度学习中非常重要的原因,因为 GPU 非常擅长做类似矩阵乘之类的运算。
X=∣∣∣∣x1x2∣∣∣∣
W=∣∣∣∣∣∣w1w4x3w2w5w6∣∣∣∣∣∣
H=f⎝⎛∣∣∣∣∣∣w1w4x3w2w5w6∣∣∣∣∣∣∣∣∣∣x1x2∣∣∣∣+b⎠⎞
不过,矩阵也不仅仅局限于神经网络的应用,同时它也可以用在计算机图形图像的应用中,比如,三维物体从取景到屏幕的显示,就需要经历一系列的空间变换,才能生成二维图像显示在显示器上。在这个计算过程中,我们都需要用到矩阵。
矩阵是非常实用的,但它正式作为数学中的研究对象出现,其实是在行列式的研究发展起来之后。英国数学家 Arthur Cayley 被公认为矩阵论的创立人,他提出的矩阵概念可能来自于行列式。但我相信另一种说法,提出矩阵是为了更简单地表达线性方程组,也就是说,矩阵是线性方程组的另一种表达。
矩阵的基本概念
线性方程组的概念很简单,上节我们已经简单提过。你在小学或中学肯定也学过二元一次方程和二元一次方程组。
ax+by=c
{a1x+b1y+C1=0a2x+b2y+C2=0
在这样一个方程组中,a1、a2、b1、b2 不能同时为 0。当我们把二元一次方程组再扩展一下,变成多元一次方程组时,我们就能得到线性方程组的一般表达,即 AX=B。
⎩⎪⎪⎨⎪⎪⎧a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯am1x1+am2x2+⋯+amnxn=bm
于是,这个线性方程组的所有系数就构成了一个 m×n 的 m 行 n 列矩阵:
A=⎣⎢⎢⎡a11a21…am1a12a22…am2…………a1na2n…amn⎦⎥⎥⎤
我们把 A 称为该方程组的系数矩阵,而当我们把等式右边的常数 b 放入矩阵后,就是下面这样:
A=⎣⎢⎢⎡a11a21…am1a12a22…am2…………a1na2n…amnb1b2…bm⎦⎥⎥⎤
这样我们就得到了 A 矩阵的增广矩阵 A ,可以表示为 (A,B),这里的 B 表示的是方程组常数项所构成的列向量,也就是 m×1 的 m 行 1 列矩阵:
B=∣∣∣∣∣∣∣∣b1b2⋯bm∣∣∣∣∣∣∣∣
如果设 X 为 n×1 的 n 行 1 列矩阵:
X=∣∣∣∣∣∣∣∣x1x2⋯xn∣∣∣∣∣∣∣∣
那么线性方程组 A,就可以表示为 AX=B 的矩阵形式。如果我们再换一种表示形式,设:a1,a2,…,an,β 表示增广矩阵 A 的列向量,则线性方程组 A 又可表示为 a1x1+a2x2+⋯+anxn=β。
线性方程组的矩阵和向量形式都是线性方程组的其他表达形式。在工作中,你可以用它们来简化求解,甚至可以提升计算效率,就如之前提到的神经网络的隐藏层的输出计算、图形图像的三维空间变换。在数学中也是同样的,你可以经常运用它们来简化求解。具体线性方程组求解的内容比较多,我们下一节课再来详细讲解求解过程。
通过前面的讲解,我相信你对矩阵有了一定的了解,现在我们再回头来看看矩阵的定义吧。
矩阵的定义是:一个 (m,n) 矩阵 A,是由 m×n 个元素组成,m 和 n 是实数,其中元素 aij,i=1,…,m,j=1,…,n 按 m 行 n 列的矩形排布方式后可以形成矩阵 A:
A=⎣⎢⎢⎡a11a21…am1a12a22…am2…………a1na2n…amn⎦⎥⎥⎤
其中 aij 属于实数 R,按通常的惯例,(1,n) 矩阵叫做行,(m,1) 矩阵叫做列,这些特殊的矩阵叫做行或列向量。
定义完矩阵后,我接着讲一个比较有趣的概念,矩阵转换(Matrix transformation)。矩阵转换经常被用在计算机图形图像的转换中,比如,一张彩色图片从 RGB 角度来说是三维的,如果要转换成灰度图片,也就是一维图片,那就要做矩阵转换。
我们来看一下矩阵转换的过程。设 Rm×n 是实数矩阵 (m,n) 的集合,A∈Rm×n 可以表示成另一种形式 a∈Rmn 。我们把矩阵的 n 列堆叠成一个长向量后完成转换。这个转换也叫做 reshape,其实就是重新调整原矩阵的行数、列数和维数,但是元素个数不变。

矩阵的运算
了解了矩阵的基本定义后,我们才能进入矩阵的运算环节,就是矩阵的加和乘。
加运算很简单,两个矩阵 A∈Rm×n,B∈Rm×n 的加运算其实就是矩阵各自元素的加。
A+B=⎣⎢⎢⎢⎢⎡a11+b11⋅⋅⋅am1+bm1……a1n+b1n⋅⋅⋅amn+bmn⎦⎥⎥⎥⎥⎤∈Rm×n
我推荐你使用 NumPy 的 einsum 来高效地做这类运算,因为它在速度和内存效率方面通常可以超越我们常见的 array 函数。
C= np.einsum(‘il, lj’, A, B)
接下来,我们一起来看看矩阵的乘。这里你需要注意,矩阵的乘和通常意义上“数之间的乘”不同,矩阵的乘有多种类型,这里我讲三种最普遍,也是在各领域里用得最多的矩阵乘。
1. 普通矩阵乘
普通矩阵乘是应用最广泛的矩阵乘,两个矩阵 A∈Rm×n,B∈Rn×k,普通矩阵则乘可以表示为 C=AB∈Rm×k,C 中元素的计算规则是矩阵 A、B 对应两两元素乘积之和。
cij=k=1∑naikbkj,i=1,…,m,j=1,…,l
我们举例来说明。C 的第一个元素 c11=a11×b11+a12×b21+a13×b31=1×1+2×2+3×3。
C=AB=[142536]⎣⎡123456⎦⎤=[1×1+2×2+3×34×1+5×2+6×31×4+2×5+3×64×4+5×5+6×6]=[14323277]
这里需要特别注意的是,只有相邻阶数匹配的矩阵才能相乘,例如,一个 n×k 矩阵 A 和一个 k×m 矩阵 B 相乘,最后得出 n×m 矩阵 C,而这里的 k 就是相邻阶数。
AB=C
但反过来 B 和 A 相乘就不行了,因为相邻阶数 m 不等于 n。
2. 哈达玛积
哈达玛积理解起来就很简单了,就是矩阵各对应元素的乘积,cij=aij×bij 。举个例子:
C=A∗B=[1425][1245]=[1∗14∗22∗45∗5]=[18825]
哈达玛积其实在数学中不常看到,不过,在编程中哈达玛积非常有用,因为它可以用来同时计算多组数据的乘积,计算效率很高。
3. 克罗内克积
克罗内克积是以德国数学家利奥波德·克罗内克(Leopold Kronecker)的名字命名的。它可以应用在解线性矩阵方程和图像处理方面,当然从更时髦的角度说,它还能用在量子信息领域,我们也称之为直积或张量积。
和普通矩阵乘和哈达玛积不同的是,克罗内克积是两个任意大小矩阵间的运算,表示为 A×B,如果 A 是一个 m×n 的矩阵,而 B 是一个 p×q 的矩阵,克罗内克积则是一个 mp×nq 的矩阵。
接下来我们需要定义一个在矩阵的乘法中起着特殊作用的矩阵,它就是单位矩阵。高等代数中,在求解相应的矩阵时,若添加单位矩阵,通过初等变换进行求解,往往可以使问题变得简单。按照百度百科的解释,单位矩阵如同数的乘法中的 1,这种矩阵就被称为单位矩阵。它是个方阵,从左上角到右下角的对角线,也就是主对角线上的元素均为 1,除此以外全都为 0。
在线性代数中,大小为 n 的单位矩阵就是在主对角线上均为 1,而其他地方都是 0 的 n×n 的方阵,它用 In 表示,表达时为了方便可以忽略阶数,直接用 I 来表示:
I1=[1],I2=[1001],I3=⎣⎡100010001⎦⎤,…,In=⎣⎢⎢⎢⎢⎡10..001..0……….…00..1⎦⎥⎥⎥⎥⎤
矩阵的性质
在了解了矩阵加和乘,以及单位矩阵后,我们是时候来看一看矩阵的性质了。了解矩阵的性质是进行矩阵计算的前提,就像我们小时候学加减乘除四则运算法则时那样。所以,这块内容对你来说应该不难,你作为了解就好,重点是之后的运算。
1. 结合律
任意实数 m×n 矩阵 A,n×p 矩阵 B,p×q 矩阵 C 之间相乘,满足结合律 (AB)C=A(BC)。这个很好理解,我就不多说了。
∀A∈Rm×n,B∈Rn×p,C∈Rp×q:(AB)C=A(BC)
2. 分配律
任意实数 m×n 矩阵 A 和 B,n×p 矩阵 C 和 D 之间相乘满足分配律 (A+B)C=AC+BC,A(C+D)=AC+AD。
∀A,B∈Rm×n,C,D∈Rn×p:(A+B)C=AC+BC,A(C+D)=AC+AD
3. 单位矩阵乘
任意实数 m×n 矩阵 A 和单位矩阵之间的乘,等于它本身 A。
∀A∈Rm×n:ImA=AIn=A
注意,这里的行和列不同,m=n 意味着,根据矩阵乘,左乘和右乘单位矩阵也不同,也就是 Im=In。
逆矩阵与转置矩阵
了解矩阵基本概念、运算,以及性质后,我来讲一讲矩阵应用中的两个核心内容——逆矩阵和转置矩阵。逆矩阵和转置矩阵在实际应用中大有用处,比如:坐标系中的图形变换运算。我们先来看下什么是逆矩阵。
逆矩阵
下面这个图你应该非常熟悉了,图中表现的是数字的倒数,2 的倒数是 21,21 的倒数是 2。
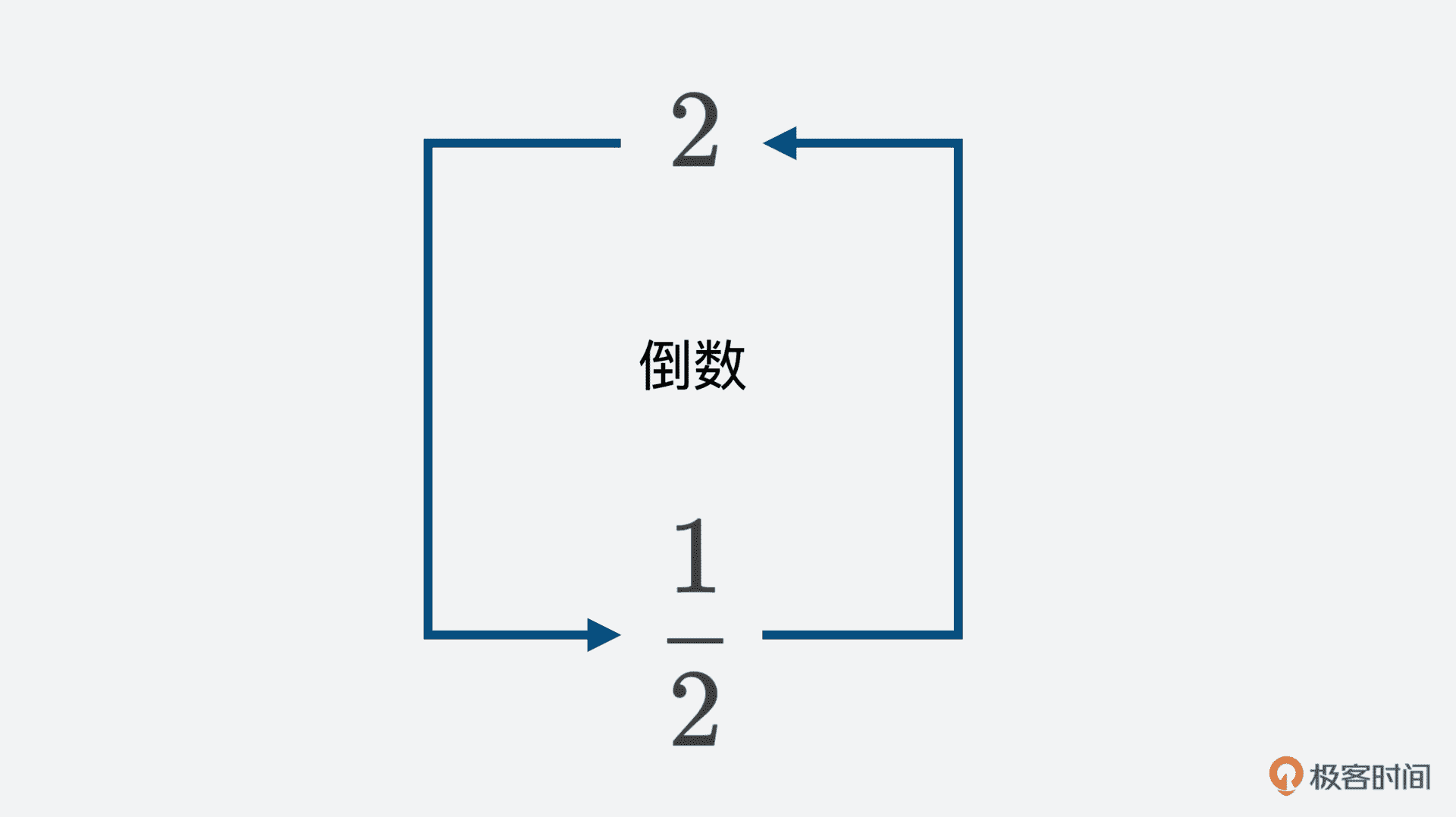
其实逆矩阵也有着类似的概念,只不过是写法不一样,我们会把逆矩阵写成 A−1。那为什么不是 A1 呢?那是因为数字 1 无法被矩阵除。

我们知道,2 乘以它的倒数 21 等于 1。同样的道理,A 乘以它的逆矩阵 A−1 就等于单位矩阵,即 A×A−1=I(I 即单位矩阵),反过来也一样,A−1×A=I。
为方便你理解,我用一个 2×2 矩阵 A 来解释一下逆矩阵的算法。首先,我们交换 a11 和 a22 的位置,然后在 a12 和 a21 前加上负号,最后除以行列式 a11a22−a12a21。
A−1=[a11a21a12a22]−1=a11a22−a12a211[a22−a21−a12a11]
那我们该如何验证这是不是正解呢?
方法其实很简单,记得刚才的公式就行,A×A−1=I。现在我们就代入公式来验证一下,A 和它的逆矩阵相乘,通过刚才的算法最终得出的结果是单位矩阵。
A×A−1=[a11a21a12a22][a11a21a12a22]−1=[a11a21a12a22][a11a22−a12a21a22a11a22−a12a21−a21a11a22−a12a21−a12a11a22−a12a21a11]=[a11a22−a12a21a11×a22+a11a22−a12a21a12×(−a21)a11a22−a12a21a21×a22+a11a22−a12a21a22×(−a21)a11a22−a12a21a11×(−a12)+a11a22−a12a21a12×a11a11a22−a12a21a21×(−a12)+a11a22−a12a21a22×a11]=[1001]
这里有一点需要特别说明,不是每一个矩阵都是可逆的。如果一个矩阵是可逆的,那这个矩阵我们叫做非奇异矩阵,如果一个矩阵是不可逆的,那这个矩阵我们就叫做奇异矩阵,而且如果一个矩阵可逆,那它的逆矩阵必然是唯一的。
还记得行列式 a11a22−a12a21 吗?如果我们要证明矩阵是可逆的,只要证明行列式不等于零就行。更高阶的逆矩阵的算法也是一样的原理。
最后,我想通过一个现实生活中的案例来让你更多地了解逆矩阵。
一个旅游团由孩子和大人组成,去程他们一起做大巴,每个孩子的票价 3 元,大人票价 3.2 元,总共花费 118.4 元。回程一起做火车,每个孩子的票价 3.5 元,大人票价 3.6 元,总共花费 135.2 元。请问旅游团里有多少小孩和大人?
首先,我们设置一些矩阵,组成线性方程 XA=B。

要解 X,我们就要先计算 A 的逆矩阵 A−1:
A−1=[33.23.53.6]−1=3×3.6−3.5×3.21[3.6−3.2−3.53]=[−988.75−7.5]
接下来再计算 X=BA−1:
[x1x2]=[118.4135.2][−988.75−7.5]=[1622]
最终,我们得出这个旅游团有 16 个小孩和 22 个大人。
这也是解线性方程组的一种方法,类似这样的计算被广泛应用在各领域中,比如建筑工程、游戏和动画的 3D 效果上。虽然现在有很多程序包封装了这类数学计算的底层实现,但如果你能很好地理解这些概念,就可以为编程或算法调优打下坚实的基础。
Last but not least,方程次序很重要,也就是说,AX=B 和 XA=B 的结果是不同的,这个一定要牢记哦!
转置矩阵
一般伴随逆矩阵之后出现的就是转置矩阵。在计算机图形图像处理中,如果要对一个物体进行旋转、平移、缩放等操作,就要对描述这个物体的所有矩阵进行运算,矩阵转置就是这类运算之一,而矩阵的转置在三维空间中的解释就相当于“得到关于某个点对称的三维立体”。所以,转置矩阵的定义很简单。
将矩阵的行列互换,得到的新矩阵就叫做转置矩阵(transpose)。转置矩阵的行列式不变。我们把 m×n 矩阵 A 的行列互换,得到转置矩阵 AT。
A=⎣⎢⎢⎡a11a21…am1a12a22…am2…………a1na2n…amn⎦⎥⎥⎤
AT=⎣⎢⎢⎡a11a12…a1na21a22…a2n…………am1am2…amn⎦⎥⎥⎤
最后,为了方便你理解,我们再总结一下逆矩阵和转置矩阵的性质。你不用死记硬背,重在理解。
- 矩阵和自身逆矩阵相乘得道单位矩阵,AA−1=I=A−1A;
- AB 两矩阵相乘的逆,等于逆矩阵 B 和逆矩阵 A 相乘,这里强调一下乘的顺序很重要,(AB)−1=B−1A−1;
- AB 两矩阵相加后的逆矩阵,不等于各自逆矩阵的相加, (A+B)−1=A−1+B−1;
- 矩阵转置的转置还是它本身,(AT)T=A;
- AB 两矩阵相加后的转置矩阵,等于各自转置矩阵的相加,(A+B)T=AT+BT;
- AB 两矩阵相乘后的转置矩阵,等于转置矩阵 B 和转置矩阵 A 的相乘,这里再次强调乘的顺序很重要,(AB)T=BTAT。
本节小结
好了,到这里矩阵这一讲就结束了,最后我再带你总结一下前面讲解的内容。
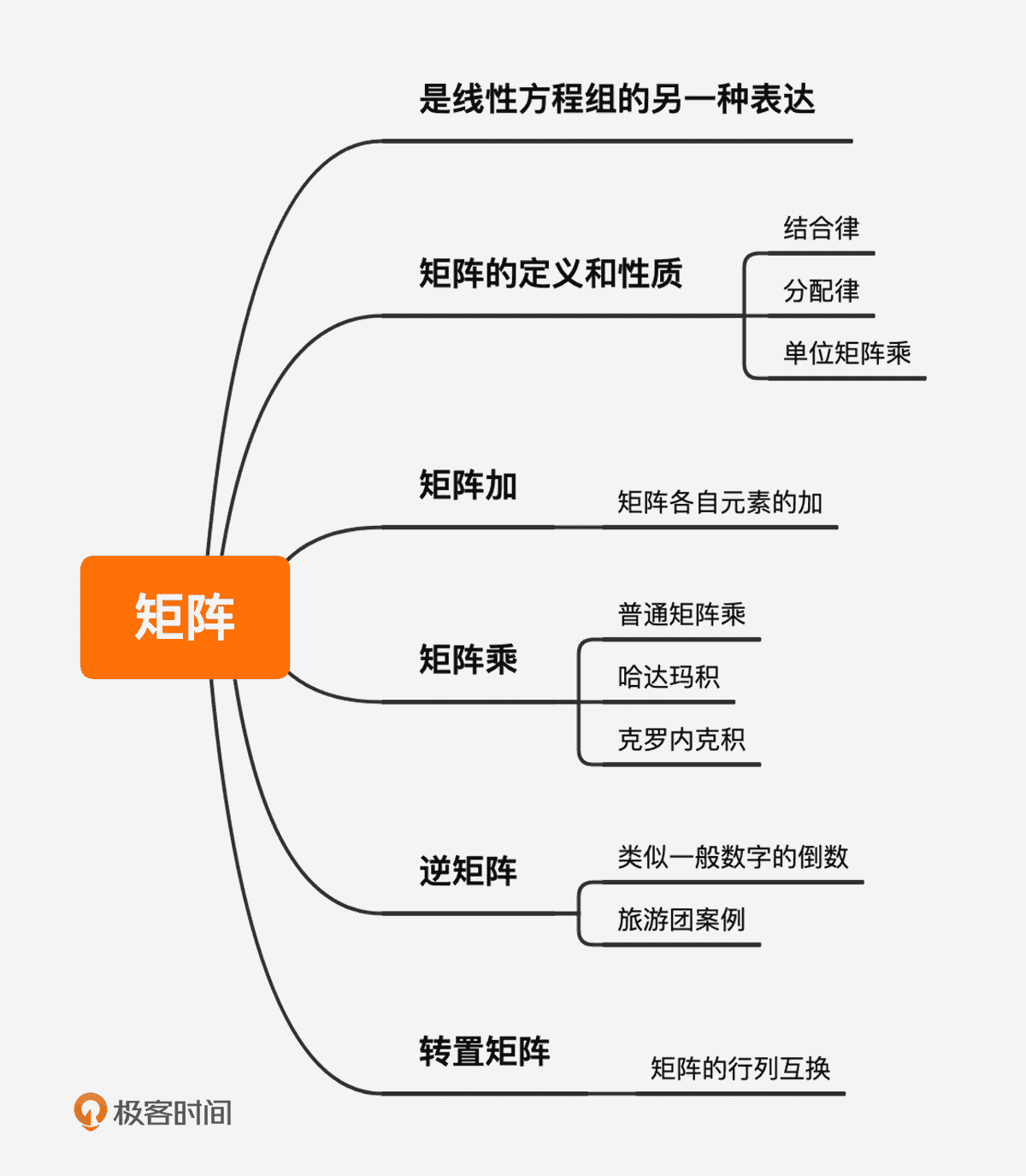
今天的知识,你只需要知道矩阵是线性方程组的另一种表达,了解和掌握矩阵的定义和性质就足够了。当然,矩阵还有很多内容,但我认为掌握了我讲的这些内容后,就为以后的一些矩阵应用场景打下了坚实的数学基础,也是下一讲的解线性方程组的前置知识。
线性代数练习场
对于 10 维列向量 x=(x1,…,x10)T, v=(v1,…,v10)T,如果要计算 y=xxT(I+vvT)x,其中 I 是 10 阶单位矩阵。你会怎么做?
友情提醒,这里有多种方式解题。你能不能找到一个最简单的方法来解这道题?虽然结果很重要,但我想说的是过程更重要,而且往往解题过程不同,从计算机角度来说,运算的效率会有极大的不同。
欢迎你在留言区晒出你的运算过程和结果。如果有收获,也欢迎你把这篇文章分享给你的朋友。
文章作者 anonymous
上次更新 2024-03-10