05|线性空间:如何通过向量的结构化空间在机器学习中做降维处理?
文章目录
你好,我是朱维刚。欢迎你跟我一起重学线性代数!
今天我们来聊一聊“线性空间”。在“基本概念”那一节课中,我讲到了向量,你也看到了,线性方程组是能够通过矩阵或向量来表达的。那为什么我们还要学习线性空间呢?
说到线性空间,其实你可以通过“空间”这个词把线性空间和我们的生活做个类比。就像我们生活在三维世界中,在这个空间中,一切物质都是运动的,而运动也是有一定规律的。这么来看的话,空间其实就是一个具有实际意义的集合,其中包含了对象和运动。
把这个理解平移到线性空间也是一样的,向量就是对象,如果把向量看成是线性空间中的点,那向量的变换就是点在空间中的运动。所以,线性空间也是一个集合,它的意义在于,赋予了向量生命和活力,只有掌握了线性空间,我们才能真正在实际运用中有的放矢。因为所有的活动都要在这个空间中发生,比如:线性空间中用到的傅立叶变换。
组
还是老样子,我们要先从学习线性空间会用到的基础知识开始讲起。
我们先来讲一下“组”,看一看组有什么性质。说到“组”,它其实是一个通用的概念,和线性空间没有什么关系,但我之所以要先说组,是因为组和空间是类似的,也是集合,性质也差不多,如果你了解了组,就更容易理解线性空间了。而且,组在计算机科学中是得到了广泛应用的,特别是在计算机密码学和图形图像处理中。
说了这么多,“组”到底是什么呢?组,其实就是包含一系列元素的集合,在对这些集合元素实施某类运算后,这个集合仍然保持着封闭性。可能这么说你会有些疑惑,我还是通过数学方法来定义组,可能会让你的思路更加清晰一些。
我们先来定义一个集合 G 和集合上的某一类运算,比如:乘 ⊗,使得 G⊗G 的结果还是属于 G,如果我们要 G:=(G,⊗) 是一个组,则需要满足以下这些条件:
1.G 在 ⊗ 运算中是封闭的,也就是:∀x,y∈G:x⊗y∈G。
2. 满足结合律,也就是:∀x,y,z∈G:(x⊗y)⊗z=x⊗(y⊗z)。
3. 恒等元素(或者叫做中性元素)e,满足:∃e∈G,∀x∈G:x⊗e=x,e⊗x=x,这里的恒等元素 e 在一般数字中你可以认为是 1,而在矩阵中就可以认为是单位矩阵。
4. 有 x 的逆元素 y,使得:∀e∈G,∃x∈G:x⊗y=e,y⊗x=e,其中 e 是恒等元素。
再补充一点,如果满足 ∀x,y∈G:x⊗y∈y⊗x,则 G:=(G,⊗) 就叫作交换组。
现在我们来做个测试,看看你是否理解了组的定义。
一个 n×n 的实数矩阵 A 和它的乘法运算是一个组吗?通过符号表达就是:(An×n,⋅)。
想要知道这个问题的答案,我们就需要用前面满足组的这几个条件来分析一下。
首先,是封闭性和结合律,从矩阵乘的定义就能直接看出来,它们是满足的;其次,我们来看恒等元素,单位矩阵就是矩阵元素,也满足组条件;最后,我们看看逆元素,假设 A 矩阵的逆矩阵 A−1 存在,那很明显,满足 AA−1=I,这里 I 就是恒等元素。
于是,我们可以说 (An×n,⋅) 是一个组,而矩阵乘不符合交换律,所以这个组并不是交换组。
向量空间
如果我们在“组”的基础上再扩展一下,就能够很顺利地来到“线性空间”。说起线性空间,它也叫作向量空间,它在一些书本和网络上的解释都是比较晦涩难懂的,但如果我们在“组”的基础上来解释它,你应该会比较容易理解了。
刚才我们说的组只包含了某一类运算,这类运算是在集合元素上的内部运算,我们把它定义为加 (+) 运算,现在再引入一类外部运算,标量乘 (⋅)。于是,你可以想象一下,我们可以把内部运算看成是加法,把外部运算看成是“缩放”,因为标量乘就是一个标量和向量相乘。如果从二维坐标系的角度来看一下,点 (1,1) 和标量 2 相乘就是 (2,2),这个就是放大效果。

在通过“组”来认识向量空间后,再从数学角度去看向量空间的定义,你应该就能完全理解了。
一个实数向量空间 V 是一个集合,它包含了两类运算,一类是加,一类是标量乘,而且运算都满足 V 的封闭性,也就是说,V 中元素的运算结果还是属于 V。
+:V+V→V⋅:λ⋅V→V
这个向量空间可以表示成 V:=(V,+,⋅),其中:
1. 向量空间 V 的 (V,+) 是一个交换组。
2.V 满足分配律:∀λ∈R,x,y∈V:λ⋅(x+y)=λ⋅x+λ⋅y;以及 ∀λ,φ∈R,x∈V:(λ+φ)⋅x=λ⋅x+φ⋅x。
3.V 外部运算满足结合律:∀λ,φ∈R,x∈V:λ⋅(φ⋅x)=(λ⋅φ)⋅x。
4.V 外部运算的恒等元素满足:∀x∈V:1⋅x=x。
在向量空间 V 中的元素 x 是向量,向量空间加运算 (V,+) 的恒等元素是零向量 0=[0,…,0]T。这里的加运算是内部运算,也叫做向量加,元素 λ 属于实数,叫做标量,外部运算乘 ⋅ 是标量乘。
好了,我给出了向量空间的一般描述和数学定义,如果你还是有一些不理解,也没有关系,我再举两个例子来加深你对向量空间的理解。
例 1:进一步理解向量加和标量乘
对于向量空间的向量加和标量乘:我们定义一个实数向量空间 Rn,n 表示向量元素:
- “加”定义为向量之间的加:x+y=(x1,…,xn)+(y1,…,yn)=(x1+y1,…,xn+yn)。加的结果还是属于向量空间 Rn。
- 标量乘就是向量乘标量:λx=λ(x1,…,xn)=(λx1,…,λxn)。
标量乘的结果还是属于向量空间 Rn。
例 2:进一步理解矩阵加和标量乘
对于向量空间的矩阵加和标量乘:我们定义一个实数向量空间 Rm×n,用 m×n 表示 m 行 n 列矩阵元素:
我们把“加”定义为矩阵之间的加。加的结果还是属于向量空间 Rm×n。
A+B=⎣⎢⎢⎢⎢⎡a11+b11⋅⋅⋅am1+bm1……a1n+b1n⋅⋅⋅amn+bmn⎦⎥⎥⎥⎥⎤
而标量乘就是矩阵乘标量。标量乘的结果还是属于向量空间 Rm×n。
λA=⎣⎢⎢⎡λa11⋅⋅λm1……λa1n⋅⋅λa˙mn⎦⎥⎥⎤
到这里,相信你应该了解了向量空间的基本概念,接下来这一讲的重头戏就要来了,它就是向量子空间。
向量子空间
为什么说向量子空间是重头戏?那是因为它在机器学习中的地位相当重要,被用在了降维算法中。这里我会分两步来讲解,先讲向量子空间的基本概念,再通过一个机器学习的例子,能让你更了解它,并灵活运用在工作实践中。
什么是向量子空间?
从“子”这个字,我们可以很直观地想到,它是被包含在向量空间中的,事实也确实如此。
已知 V:=(V,+,⋅) 是一个向量空间,如果 U⊆V,U=0,那么 U:=(U,+,⋅) 就是 V 的向量子空间,或者叫做线性子空间。向量子空间 U 自然继承 V 的许多属性,其中包括:交换组的属性、分配律、结合律和中性元素。除此以外,要判断 U 是不是向量子空间,我们还需要这两个条件:
1.U=0,但 0∈U。
2. U 的封闭性满足外部运算:∀λ∈R,∀x∈U:λx∈U,同时满足内部运算:∀x,y∈U:x+y∈U。
介绍完向量子空间基本概念后,我们一起来通过一个例子来巩固一下所学的知识,看看你是否已经掌握了向量子空间。
请你观察下面列举的 A、B、C 三张图像,里面有 R2 的向量子空间吗?
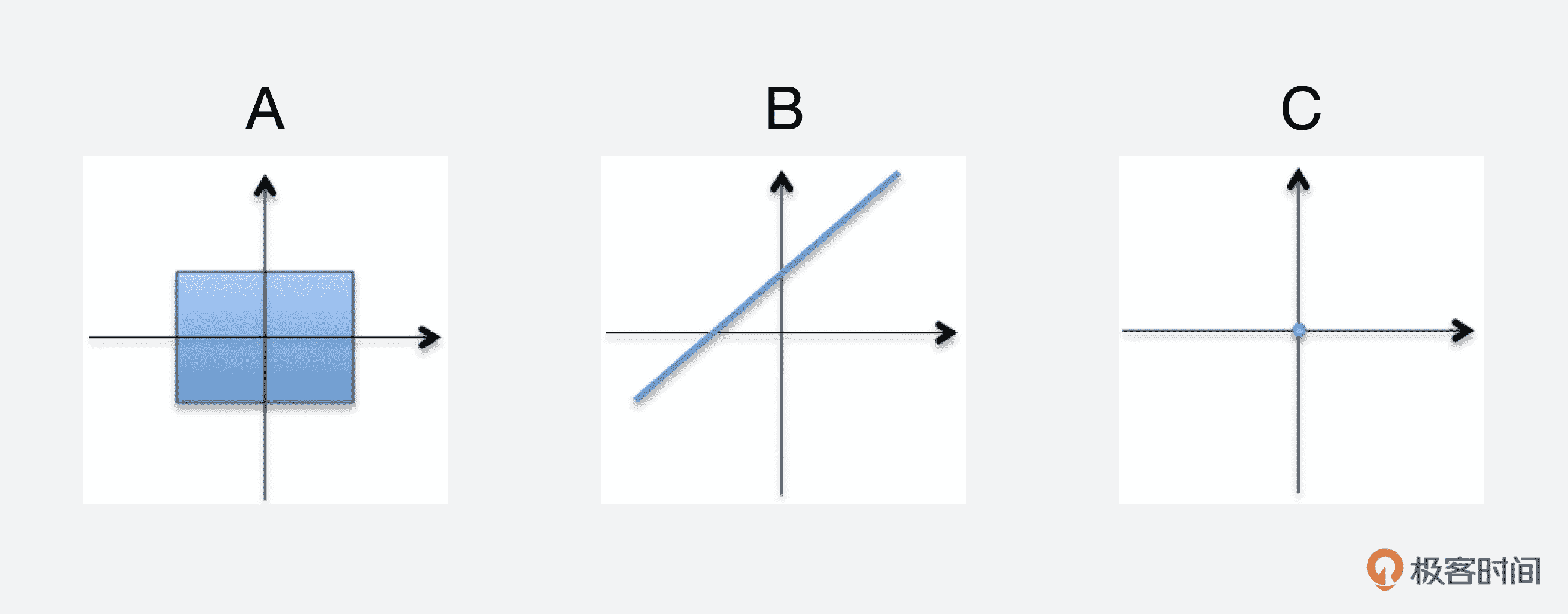
这里我不会给出答案,你可以自己思考一下,友情提醒:A、B、C 中只有一个是向量子空间。
机器学习中的向量子空间
结合实践来看向量子空间的时候到了。在机器学习中,直接计算高维数据困难重重,一方面是数据处理和分析困难,使得数据可视化几乎不可能;另一方面是因为数据存储量太大,计算要付出的代价太高。
所以,我们要从向量空间中去除冗余数据,形成向量子空间。这样数据存储量就被极大地压缩了,处理和分析数据也简单了很多。因为高维数据中其实有很多维是冗余的,它们可以被其它维组合表示,也就是“降维”。
降维就是利用结构化和相关性,在尽量保证信息不损失的情况下,转换数据表现形式,让数据更“紧凑”。换句话说,你可以把降维看成是数据压缩技术,类似图像的 jpeg 和音频的 MP3 压缩算法。或者简单地说,降维就是将数据投射到一个低维子空间,比如:三维数据集可以降成二维,也就是把数据映射到平面上。
机器学习中运用最多的降维算法就是主成分分析,简称 PCA(Principal Component Analysis),也叫做卡尔胡宁 - 勒夫变换(Karhunen-Loeve Transform)。它是一种用于探索高维数据结构的技术,已经存在超过 100 年了,但至今仍然广泛被使用在数据压缩和可视化中。
我们来看一个例子:假设你负责的是机器学习算法,而你的应用场景是车辆的牌照识别,也就是 OCR(Optical Character Recognition)光学字符识别。在这个场景中,大街上的摄像头必须实时捕捉运动车辆的牌照,一旦发现问题车辆就需要快速识别牌照,并移交交警监管部门来做进一步处理。你会怎么处理呢?
牌照被拍下后就是图片,为了减小图像原始数据量,减少后续处理时的计算量,这些图片首先需要进行经过灰度处理(牌照只需要数字,不需要对彩色图像的 RGB 三个分量都进行处理),处理后就会变成类似这样的形式:

假定每个数字是一个 28∗28 尺寸的灰度图片,包含 784 个像素,那每张灰度数字图片就是一个向量,这个向量就有 784 个维度,可以表示成 x∈R784,而你的样本库少说也有几十万个样本数据,如果按一般的方法是不可能做到实时识别的。所以,这样的场景就需要使用 PCA 来压缩数据,进行大幅度降维。
这里我们简单一些,从二维的角度来看看 PCA。在 PCA 中,最关键的就是寻找数据点 xn 的相似低维投影 yn,而 yn 就是子向量空间。
考虑 R2 和它的两个基,e1=[1,0]T、e2=[0,1]T,x∈R2 能够表示成这两个基的线性组合(“基”会在第 7 节课中详细介绍)。
[53]=5e1+3e2
于是,相似低维投影 yn 就可以表示成下面这种形式。
yn=[0z]∈R2,z∈R
同时,yn 也可以写成这样的形式:yn=0e1+ze2。
这里的 z 就是我们要找的值,而 yn 就是一个向量子空间 U,它的维度是一维。最后,我们再通过下图来更直观地说明一下 PCA 的过程。

图的左边是原始向量空间 x,经过压缩后,我们找到了子向量空间 z,z 经过重构后,形成了最终的向量空间 y,y 还是属于原来的向量空间,但 y 却拥有比 x 更低的维度表现。
从数学的角度看,我们其实就是在寻找 x 和 z 之间的线性关系,使得 z=BTx,以及 y=Bz,其中 B 是矩阵。如果我们从数据压缩技术方向来看就更容易理解了,图中的左边箭头是编码过程,也就是压缩,右边的箭头是解码过程,也就是映射,而矩阵 B 就是把属于 RM 向量空间的低维的 z,映射回原来的向量空间 RD。同理,矩阵 BT 就是把属于原来 RD 向量空间的高维 x 压缩成低维的 z。
本节小结
好了,到这里线性空间这一讲就结束了,最后我再总结一下前面讲解的内容。
今天的知识很重要,实践中都是围绕向量空间展开的,也就是说向量空间是实践的基本单位,你也一定要掌握子向量空间,因为现实中数据都是高维度的,从向量空间降维后找到子向量空间,这样就能大大提高数据运算和分析的效率。
再次特别提醒:这一讲非常重要,因为后面几讲都是围绕向量空间展开的,如果你哪里没看懂,一定要多看几次,确保完全明白了。有任何问题,你也可以随时在留言区向我提问。
线性代数练习场
之前我讲了一个现实的向量空间降维场景:车辆的牌照识别,这里,我们通过另一个现实场景,来练习一下向量空间降维的思维。
目前市场上语音识别的应用有很多,比如:天猫精灵、苹果 Siri、小爱等等,而语音识别涉及的技术有很多,有语言建模、声学建模、语音信号处理等等。在语音信号处理中,语音声波通过空气传播,并被麦克风捕获,麦克风将压力波转换为可捕获的电活动。我们对电活动进行采样,用以创建描述信号的一系列波形采样。
采样是数据收集的过程,数据收集后需要做数据预处理,而预处理的关键一步就是特征提取,现在请你从“特征提取”的方向上思考下,有哪些和目前所学到的数学知识有关?
友情提醒:特征提取就是数字化过程,也是向量化后形成向量空间的过程。
欢迎在留言区写出你的思考,我会及时回复。如果有收获,也欢迎你把这篇文章分享给你的朋友。
文章作者 anonymous
上次更新 2024-03-10