10|解析几何:为什么说它是向量从抽象到具象的表达?
文章目录
你好,我是朱维刚。欢迎你继续跟我学习线性代数,今天我们要讲的内容是“解析几何”。
前面所有章节我们都是围绕向量、矩阵,以及向量空间来展开的。但这一节课有点不一样,我要讲的是解析几何,它使得向量从抽象走向了具象,让向量具有了几何的含义。比如,计算向量的长度、向量之间的距离和角度,这在机器学习的主成分分析 PCA 中是非常有用的。
范数
讲解析几何我们得从“范数”开始讲起。
因为很多人看到几何向量的第一反应就是,它是从原点开始的有向线段,并且向量的长度是这个有向线段的终端和起始端之间的距离。而范数,就是被用来度量某个向量空间或矩阵中的每个向量的长度或大小的。
现在,我们先来看一下范数的数学定义:一个向量空间 V 上的一个范数就是一个函数,它计算 V 中的每一个向量 x 的长度,用符号来表示的话就是:∥x∥∈R,它满足三种性质:
- 正齐次性:如果输入参数扩大正 λ 倍,其对应的函数也扩正大倍。设 λ∈R,x∈V,∥λx∥=∣λ∣∥x∥;
- 次可加性:类似三角不等式,两边之和大于第三边。设 x,y∈V,∥x+y∥≤∥x∥+∥y∥;
- 正定性:向量 x 的长度一定大于等于零。∥x∥≥0。
看到这里,你也许会问,范数似乎和以前老师教的向量的模一样啊。先别急,它们还真有那么一点关系,你听我慢慢道来。由于范数是度量某个向量空间或矩阵中的每个向量的长度或大小的,所以它和向量空间维度是有关系的,于是,我们可以把范数写成这样的模式来区分不同维度的大小计算:L1,L2,…,L∞。
- L1 范数:曼哈顿范数,也叫曼哈顿距离,设 x∈Rn,得到下面这个表达式。
∥x∥1=i=1∑n∣xi∣
- L2 范数:欧式范数,也叫欧式距离,设 x∈Rn,得到下面这个表达式。
∥x∥2=i=1∑nxi2
- L∞ 范数:切比雪夫范数,也叫切比雪夫距离,设 x∈Rn,得到下面这个表达式。
∥x∥∞=max(∣x1∣,∣x2∣,…,∣xn∣)
我们发现,向量的模和 L2 范数的计算方式都是一样的,都表示的是欧氏距离,所以,我们可以简单地认为向量的模等于 L2 范数。而其他的范数模式和向量的模则没有任何关系。
内积
学习解析几何时,我们必须掌握的第二个概念就是内积。
如果说范数是模式,是用来描述向量长度或大小的概念性表达,那么内积可以让我们很直观地了解一个向量的长度、两个向量之间的距离和角度,它的一个主要目的就是判断向量之间是否是正交的,正交这个概念我们会在后面讲解。
点积
我们从特殊到一般,先来看点积,它和第三篇矩阵中说的“普通矩阵乘”形式一样,点积是特殊的内积,为什么说它特殊呢?那是因为在表示两个向量之间的距离时,它就是大家熟悉的欧式距离,点积可以表示成这样的形式:
xTy=i=1∑nxiyi
其他内积
除了点积外,我们再来看另一个不同的内积:设内积空间 V 是 R2,定义内积 ⟨x,y⟩=x1y1−(x1y2+x2y1)+2x2y2,一看便知这个和点积完全不同。
内积空间
最后,我们再来看一般内积和内积空间。因为解析几何关注的是向量的长度、两个向量之间的距离和角度,所以,我们要在原来向量空间上加一个额外的结构,这个额外结构就是内积,而加了内积的向量空间,我们就叫做内积空间。
为了表达方便,我们可以把内积写成 ⟨ ⋅,⋅⟩ 这样的形式,那么内积空间 V 可以被表示成这样:(V,⟨ ⋅,⋅⟩)。这时,如果一般内积由点积来表达,那这个向量空间就变成了更具体的欧式向量空间。
接下来看下内积空间有什么性质?我们定义一个内积空间 V 和它的元素 x、y、z,以及一个 c∈R:
- 满足对称性:x 和 y 的内积等于 y 和 x 的内积,⟨x,y⟩=⟨y,x⟩;
- 满足线性性:x 和 y+cz 的内积等于,x 和 y 的内积,与 x 和 z 的内积乘以 c 后的和,
⟨x,y+cz⟩=⟨x,y⟩+c⟨x,z⟩;
- 满足正定性:x 和 y 的内积大于等于零,⟨x,y⟩≥0。
对称正定矩阵
内积还定义了一类矩阵,这类矩阵在机器学习中很重要,因为它可以被用来判定多元函数极值,而在深度学习中,它更是被用来获取最小化损失函数,我们把这类矩阵叫做对称正定矩阵。
对称正定矩阵的定义是:如果一个对称矩阵 A 属于方阵 Rn×n,对任意非零向量 x,都有 xTAx>0,那么 A 就是对称正定矩阵。
我们来看两个例子,判断它们是不是对称正定矩阵。
第一个例子,请你回答下面这个矩阵是对称正定矩阵吗?
A=[9665]
答案:是的,它是对称正定矩阵。因为 xTAx>0。
xTAx=[x1x2][9665][x1x2]=(3x1+2x2)2+x22>0
第二个例子,请你看下面这个矩阵是对称正定矩阵吗?
A=[9663]
答案:不是的,它只是对称矩阵。因为 xTAx 可能小于 0。
xTAx=[x1x2][9663][x1x2]=(3x1+2x2)2−x22
长度、距离和角度
前面我们通过范数讲了向量的长度,但从内积的角度来看,我们发现,内积和范数之间有着千丝万缕的关系。我们来看看下面这个等式。
∥x∥=⟨x,x⟩
从这个等式我们发现,内积可以用来产生范数,确实是这样。不过,不是每一个范数都能被一个内积产生的,比如:曼哈顿范数。接下来,我们还是来关注能由内积产生的范数上,从不同的角度来看看几何上的长度、距离和角度的概念。
我们先用内积来计算一个向量的长度,比如:向量 x=[11]T,我们可以使用点积来计算,计算后得出 x 的范数是 2,具体计算过程是这样的:∥x∥=xTx=12+12=2。
接着,我们再来看一下向量之间的距离,一个内积空间 V,(V,⟨ ⋅,⋅⟩),x 和 y 是它的两个向量,那么 x 和 y 之间的距离就可以表示成:d(x,y)=∥x−y∥=⟨x−y,x−y⟩。
如果用点积来计算 x 和 y 之间的距离,那这个距离就叫做欧式距离。
再接着,来看看两个向量之间的角度。我们使用柯西 - 施瓦茨不等式(Cauchy-Schwarz Inequality)来表示内积空间中两个向量 x 和 y 之间的角度:a。
−1≤∥x∥∥y∥⟨x,y⟩≤1
取值是从 −1 到 1 之间,那么角度就是从 0 到 π 之间,我们用 cos 来表示就是:
cos(a)=∥x∥∥y∥⟨x,y⟩
其中 a 就是角度,a 的角度取值是 0 到 π 之间。我们很容易就能发现,其实两个向量之间的角度,就是告诉了我们两个向量之间方向的相似性。例如:x 和 y=4x,使用点积来计算它们之间的角度是 0,也就是说它们的方向是一样的,y 只是对 x 扩大了 4 倍而已。
现在,我们通过一个例子,再来更清楚地看下两个向量之间角度的计算,设 x=[11]T,y=[12]T,使用点积来计算,我们得出:
cos(a)=⟨x,x⟩⟨y,y⟩⟨x,y⟩=xTxyTyxTy=103
那么,这两个向量之间的角度如下。
arccos(103)≈0.32
我们可以用图来更直观地表达一下。
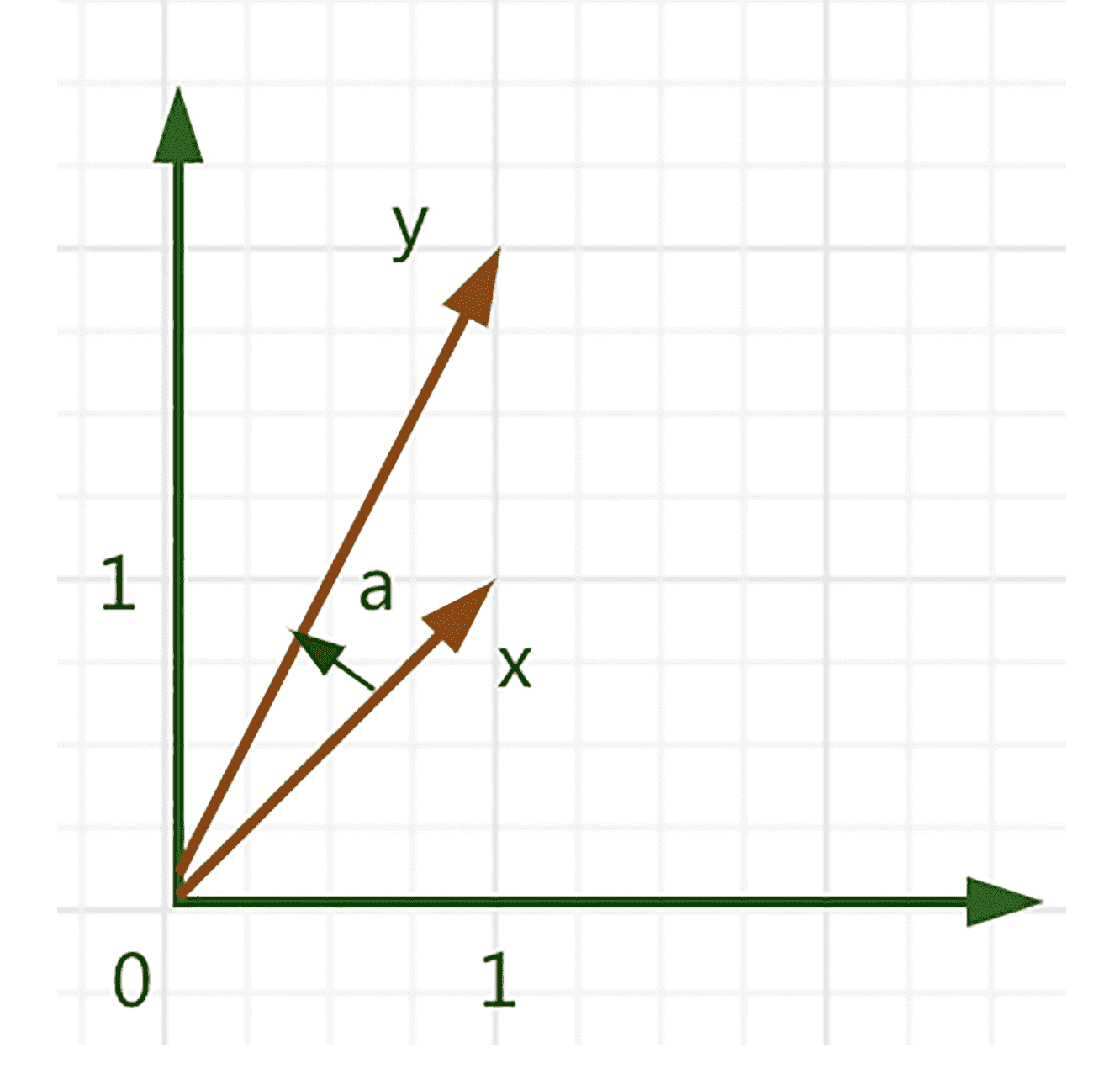
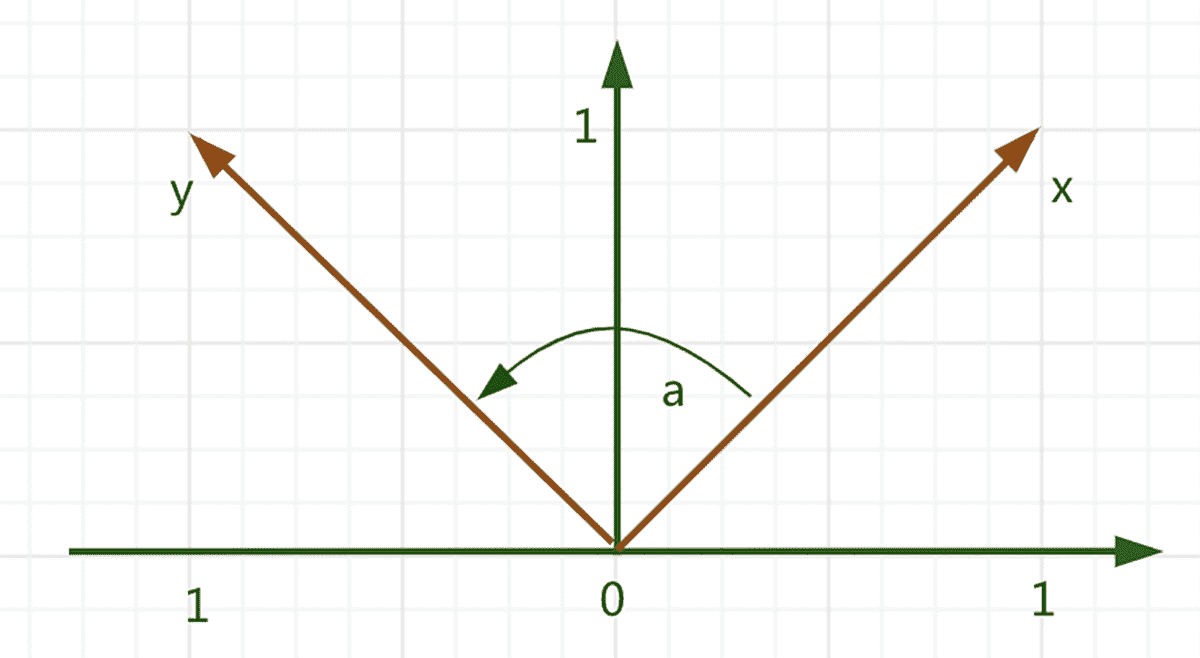
于是,我们最后可以引出一个概念,也就是我们在一开始提到的正交性。如果两个向量 x 和 y 内积等于 0,⟨x,y⟩=0,那么 x 和 y 是正交的,这可以写成:x⊥y。再如果,x 和 y 的范数都等于 1,∥x∥=∥y∥=1,也就是说,如果它们都是单位向量,那么 x 和 y 就是标准正交的。
我们用图来更直观地表达一下。
正交投影
在理论讲解之后,我们要来了解一下解析几何在实践中经常运用的概念——正交投影,它是一种重要的线性变换,在图形图像、编码理论、统计和机器学习中扮演了重要角色。
在机器学习中,数据一般都是高维的。众所周知,高维数据是很难来分析和可视化的。而且,不是所有的高维数据都是有用的,可能只有一些数据包含了大部分的重要信息。
正交投影就是高维到低维的数据投影,在第 5 节课线性空间中,我简单介绍了高维数据投影到低维后,我们就能在低维空间更多地了解数据集、提炼相关模式。而在机器学习中,最普遍的降维算法——PCA 主成分分析,就是利用了降维的观点。
接下来,我开始讲解正交投影,在给出定义之前,先从一张图来了解会更直观。
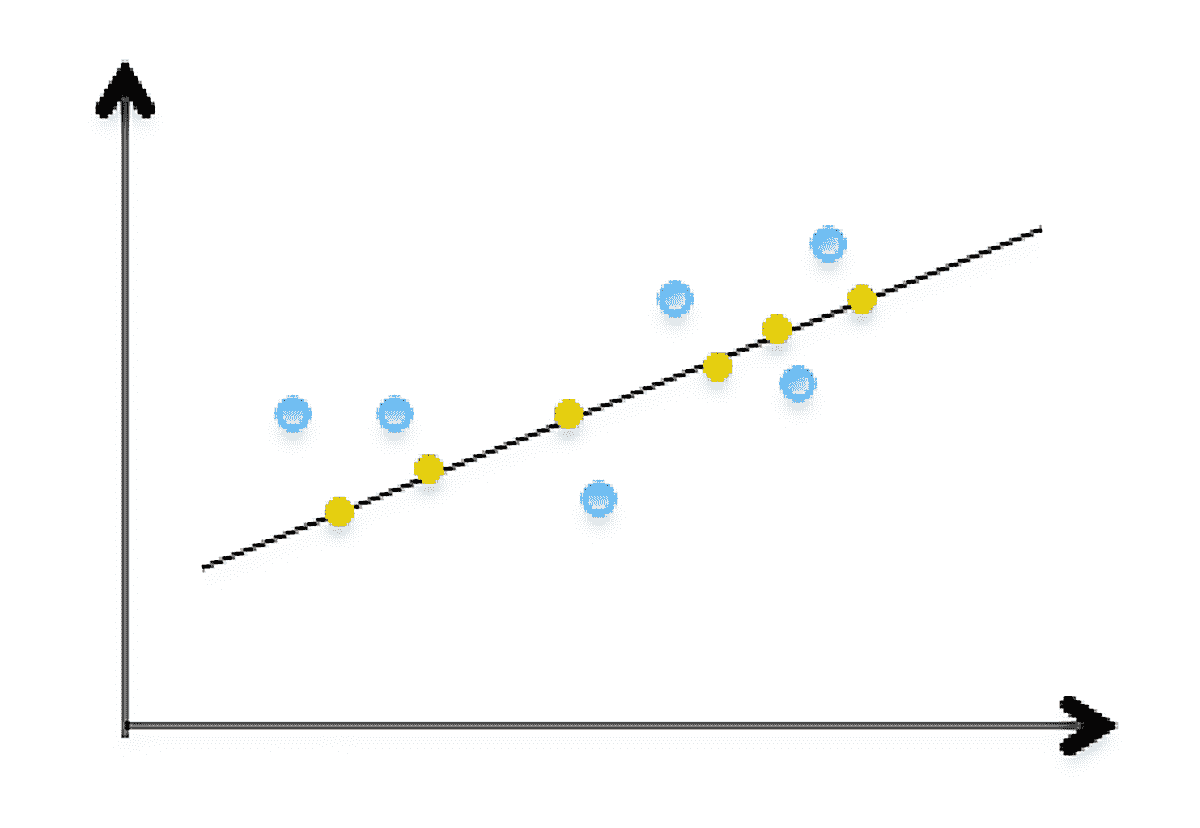
图中的蓝点是原二维数据,黄点是它们的正交投影。所以,实际降维后,在一维空间中就形成了这条黑线表示,它近似地表达了原来二维数据表示的信息。
现在我们可以来看一下投影的定义:V 是一个向量空间,U 是 V 的一个向量子空间,一个从 V 到 U 的线性映射 Φ 是一个投影,如果它满足:Φ2=Φ∘Φ=Φ。因为线性映射能够被变换矩阵表示,所以,这个定义同样适用于一个特殊类型变换矩阵:投影矩阵 PΦ,它也满足:PΦ2=PΦ。
投影到一维子空间上(线)
接下来,我们来看看如何投影到一维子空间,也就是把内积空间的向量正交投影到子空间,这里我们使用点积作为内积。
假设有一条通过原点的线,这条线是由基向量 b 产生的一维子空间 U,当我们把一个向量 x 投影到 U 时,需要寻找另一个最靠近 x 的向量 ΦU(x)。还是老样子,我们通过图来看一下。
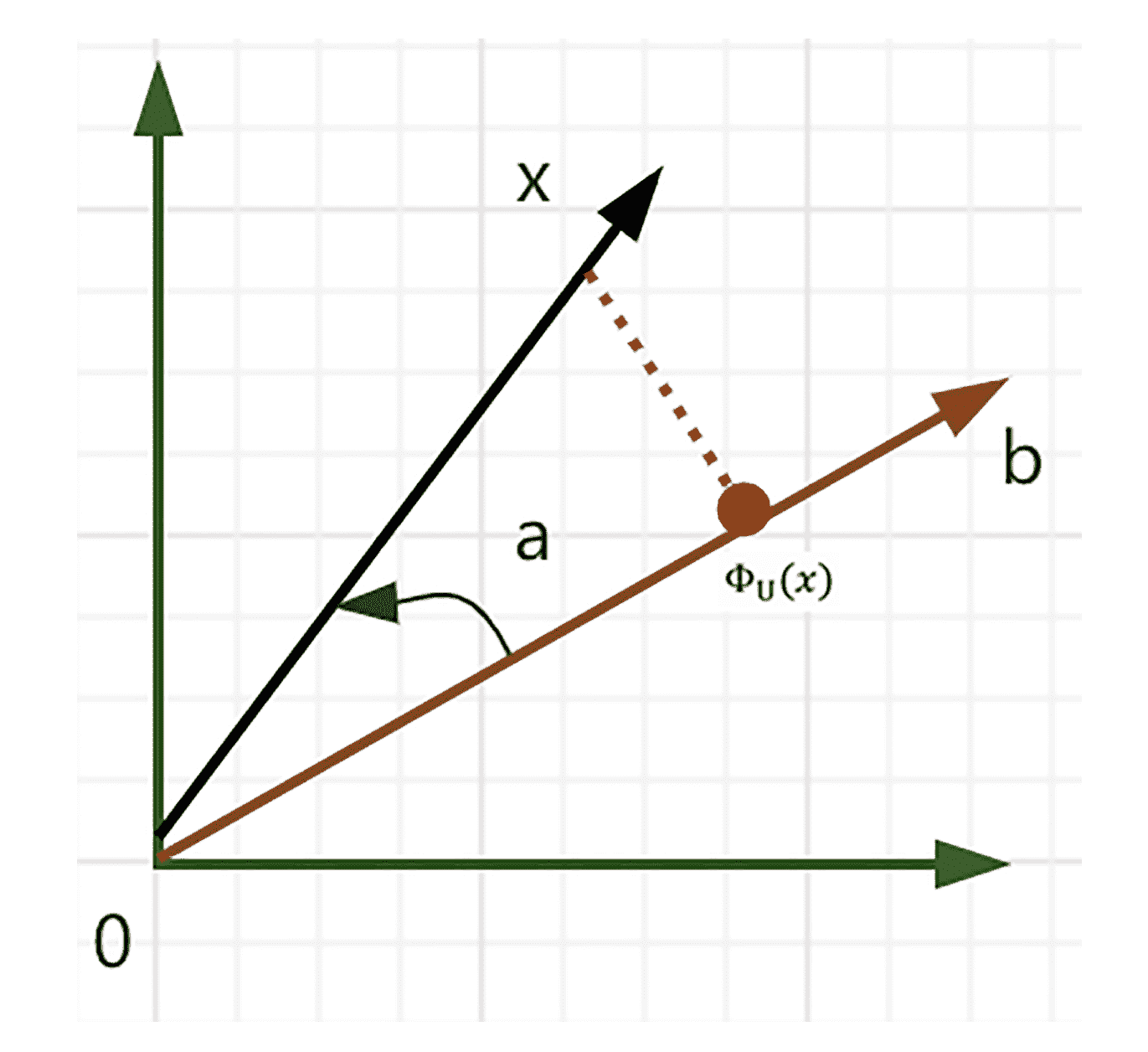
首先,投影 ΦU(x) 靠近 x,也就是要找出 x 和 ΦU(x) 之间的 ∥x−ΦU(x)∥ 最小距离,从几何角度来说,就是线段 ΦU(x)−x 和 b 正交,满足等式:⟨ΦU(x)−x,b⟩=0。其次,投影 ΦU(x) 必须是 U 的一个元素,也就是,基向量 b 的一个乘来产生 U,ΦU(x)=λb。
于是,我们可以通过三个步骤来分别得到 λ、投影 ΦU(x) 和投影矩阵 PΦ,来把任意 x 映射到子空间 U 上。
第一步,计算 λ,通过正交条件产生这样的等式:
⟨x−ΦU(x),b⟩=0。因为 ΦU(x)=λb,所以它可以转变成:⟨x−λb,b⟩=0。
利用内积的双线性:⟨x,b⟩−λ⟨b,b⟩=0,我们得到:
λ=⟨b,b⟩⟨x,b⟩=∥b∥2⟨b,x⟩
然后,我们通过点积得到:
λ=∥b∥2bTx
如果 ∥b∥=1,那 λ 就等于 bTx。
接着第二步,是计算投影点 ΦU(x)。从 ΦU(x)=λb,我们得到:
ΦU(x)=λb=∥b∥2⟨x,b⟩b=∥b∥2bTxb
通过点积来计算,我们就得到了 ΦU(x) 的长度:
∥ΦU(x)∥=∥b∥2∣∣bTx∣∣∥b∥=∣cos(a)∣∥x∥∥b∥∥b∥2∥b∥=∣cos(a)∥x∥
这里的 a,是 x 和 b 之间的夹角。
最后第三步,是计算投影矩阵 PΦ,投影矩阵是一个线性映射。所以,我们可以得到:ΦU(x)=PΦx,通过 ΦU(x)=λb,我们可以得到:
ΦU(x)=λb=bλ=b∥b∥2bTx=∥b∥2bbTx
这里,我们立即可以得到投影矩阵 PΦ 的计算等式:
PΦ=∥b∥2bbT
本节小结
这一节课覆盖的知识点有点多,因为要把解析几何的知识点,浓缩到核心的几个点来讲解是一项艰巨的任务。不过不要怕,前面的几个知识点都是为这一节的重点“正交投影”来铺垫的。范数,被用来度量某个向量空间或矩阵中的每个向量的长度或大小,而内积让我们很直观地了解一个向量的长度、两个向量之间的距离和角度,以及判断向量之间是否是正交的。
所以,希望你能掌握范数和内积的理论知识,并把它和正交投影结合,运用在一些实践应用场景中,比如:3D 图形图像的坐标变换、数据压缩,以及机器学习的降维。
线性代数练习场
请用之前学到的正交投影的投影矩阵算法,来计算一条线上的投影矩阵 PΦ。
这条线通过原点,由基 b=[122]T 产生,PΦ 计算后,再通过一个 x 来验证一下它是否在 b 产生的子空间中,我们取 x=[111]T。
欢迎在留言区晒出你的运算结果,我会及时回复。同时,也欢迎你把这篇文章分享给你的朋友,一起讨论、学习。
文章作者 anonymous
上次更新 2024-03-10